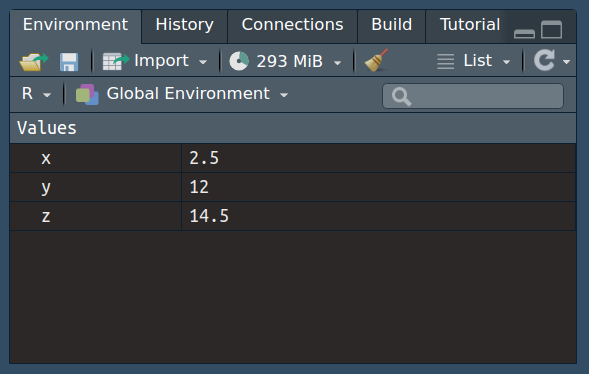
x <- 2.5 # ohne Ausgabe des Werts
(y <-12) # mit Ausgabe des Werts[1] 12Wir können einer Variablen mithilfe des Zuweisungspfeils <- ein R-Objekt zuweisen. Im einfachsten Fall ist das ein einzelner Wert, später werden das auch Vektoren, Datentabellen, Listen, Funktionen, etc. sein.
x <- 2.5 # ohne Ausgabe des Werts
(y <-12) # mit Ausgabe des Werts[1] 12Im obigen Beispiel wird x die Zahl 2.5 zugewiesen und yder Wert 12. Dabei sei angemerkt, dass der Punkt . in R der Dezimaltrenner ist! Durch die runden Klammen um den gesamten Ausdruck wird das zugewiesene Objekt auch ausgegeben, ohne die Klammern wird das Objekt nicht ausgegeben.
(z <- x + y)[1] 14.5Im letzten Beispiel werden aus den zuvor definierten Objekten x und y das Objekt z gebildet. Die Zuweisung <- bindet nur schwach, so dass die jeweils rechten Seiten der Ausdrücke zuerst ausgewertet werden (im obigen Beispiel die Addition von x und y) bevor die Zuweisung erfolgt.
Bei der Benennung von Objekten müssen ein paar Regeln beachtet werden, da Objekte in R nicht ohne weiteres beliebige Namen erhalten können. Man spricht von R-konformen Objektnamen wenn diese die folgenden Regeln erfüllen: Objektnamen dürfen
.), Unterstriche (_) und Zahlen enthalten,_ beginnen.Objekte, die mit einem Punkt . beginnen, sind versteckt, das heißt sie sind nicht im Environment und nur mit ls(all.names = TRUE)zu sehen.
Objektnamen sind case-sensitive, das heißt Groß- und Kleinschreibung wird von R unterschieden.
Drei <- 3
dreiError: Objekt 'drei' nicht gefundenWelche der eigenen Objekte R kennt kann man sich unter Environment im RStudio ansehen oder alternativ mit der Funktion ls().
Mit dem Besen (RStudio, Environment) können alle Objekte gelöscht werden; mit der Funktion rm() (Eingabe in die Konsole) können auch einzelne Objekte gelöscht werden.
Damit kann die Konsole von R wie ein überdimensionierter Taschenrechner genutzt werden. Es ist darauf zu achten, dass der Punkt (.) der Dezimaltrenner ist und nicht das Komma (,). Durch das Komma werden zum Beispiel Argumente in einer Funktion voneinander getrennt (siehe Beispiel unten).
Schon in der 5. Klasse lernt man in der Arithmetik, die Regel Punkt- vor Strichrechnung. Dies bedeutet, dass der Ausdruck a + b \cdot c das gleiche ist wie a + (b \cdot c). Durch die Regel wird also eine implizite Klammerung festgelegt. Dies nennt man die Operatorrangfolge (oder auch die Präzedenz). Legt man nun noch fest ob die Terme gleicher Bindungsstärke von links nach rechts oder von rechts nach links ausgewertet werden, können beliebige arithmetische Terme auf eindeutige Weise ausgewertet werden. Letzteres nennt man die Assoziativität der Operatoren.
2+3*4 # Plus, Mal (Punkt vor Strich)[1] 1410/5/2 # Dividieren (von links nach rechts ausgewertet)[1] 12^3^2 # Exponenzieren (von rechts nach links ausgewertet)[1] 512(2^3)^2 # runde Klammern zum explizieten Gruppieren bei Rechnungen[1] 642.5*4 # der Punkt (.) ist der Dezimaltrenner[1] 10Beim Programmieren kommen wir nicht mit der einfachen Regel Klammern vor Exponenten vor Punkt- vor Strichrechnung (wie die Regel dann am Ende der Schullaufbahn heißt) aus, da es noch mehr wichtige Operatoren gibt.
In der folgenden Liste sind (fast) alle Operatoren aufgeführt. Bei manchen ist im Moment vielleicht noch nicht klar warum wir diese benötigt, aber im Laufe des Kurses werden wir die meisten der Operatoren benötigen.
Für die Tabelle gilt:
?Syntax.
| Operator | Bedeutung | Assoziativität |
|---|---|---|
:: / :::
|
Zugriff auf Funktionen in Namespace | |
$ / @
|
Komponenten extrahieren | |
[ / [[
|
Indizieren | |
^ / **
|
Exponenzieren: a^b / a**b ist a^b
|
rechts nach links |
+x / -x
|
Vorzeichen (unärer Operator) | links nach rechts |
: |
:-Operator (binär, Erzeugung von numerischen Vektoren) |
|
%% / %/%/ … / |>
|
Modulo / Ganzzahlige Division / sonstige “%”-Operatoren / Pipe |
links nach rechts |
* / /
|
Multiplikation, Division | links nach rechts |
+ / -
|
Addition, Subtraktion (binärer Operator) | links nach rechts |
== / != / > / >= / < / <=
|
Vergleiche | links nach rechts |
! |
Logisches NICHT | links nach rechts |
& |
Logisches UND | links nach rechts |
| |
Logisches ODER | links nach rechts |
-> |
Zuweisung rechts | links nach rechts |
<- |
Zuweisung links | rechts nach links |
= |
Zuweisung links | rechts nach links |
? |
Hilfe (unärer und binärer Operator) |
-2^2^3 [1] -256Durch das Setzen von runden Klammern kann eine andere Reihenfolge, komplett analog zur Mathematik, erzwungen werden:
((-2)^2)^3[1] 64Wenn man die Operatorrangfolge oder die Assoziativität nicht (gut) kennt, so ist es ratsam Klammern zu setzen um Fehler zu vermeiden.
-2 zu setzen, um einerseits die Lesbarkeit zu verbessern und andererseits Fehler zu reduzieren.3*-2[1] -6* und Division / linksassoziativ und haben die gleiche Bindungsstärke. Der Ausdruck10/5*2/4[1] 1wird also schrittweise von links nach rechts ausgeführt, entspricht damit dem Ausdruck
((10/5)*2)/4[1] 1x <- 3*(2+1)
x[1] 9<- und = rechtsassoziativ sind, also von rechts nach links abgearbeitet werden, können mehrere Zuweisungen gleichzeitig gemacht werden. Im unteren Beispiel wird x die Zahl 5 zugeordnet und dann dem y der Wert, den das x hat:y <- x <- 5
y[1] 5und analog kann man mit -> mehrere Zuweisungen nach rechts machen.
6 -> y -> z
z[1] 6|>, der in Kapitel 5.5 noch erklärt wird, muss man ein wenig vorsichtig sein, wenn arithmetische Operationen involviert sind. Auch hier sollten wir immer Klammern setzen um Fehler zu vermeiden.3*16 |> sqrt() # ist das gleiche wie 3*sqrt(16), da |> stärker bindet als *, aber[1] 1216^2 |> sqrt() # ist das gleiche wie sqrt(16^2), da ^ stärker bindet als |> [1] 16:: bzw den ::: Operator. Beispielweise sind durch das Laden von Tidyverse die Funktion filter() bzw. lag() aus dem Paket stats nicht mehr direkt zugängig. Möchten wir diese verwenden, so müssen wir stats::lag() aufrufen. Die Operatoren :: bzw. ::: (der Unterschied ist derzeit nicht wichtig!) binden stärker als alle anderen Operatoren.
lag() und filter() aus dem stats-Paket maskiert, das heißt, wenn man die Funktion filter() aufruft wird nun die Funktion aus dem Tidyverse genutzt. Möchte man die Funktion lag() oder filter() aus dem Paket stats nutzen, so muss man den Namespace angeben: stats::lag() oder stats::filter().
Das Konzept des Namespacings ist für diesen Kurs nicht weiter relevant und soll auch nicht weiter vertieft werden.
Markieren sie die wahren Aussagen!
%>% bzw. auch die native Pipe |> binden genau so stark wie alle %-Operatoren.<- bindet stärker als =. Das heißt während in die Zuweisungen a = b <- 2 beiden Objekten die 2 zugeordnet ist, liefert a <- b = 2 einen Fehler.|> bindet schwächer als der :-Operator, daher wird dieser zuerst ausgeführt und danach die Funktion sqrt().- bindet stärker als Multiplakation und Division.Markieren sie die wahren Aussagen!
! ist das logische NICHT, das nur ein Argument hat. Der Operator wird von links nach rechts ausgewertet.! bindet stärker als das ODER !, daher ist der Ausdruck TRUE - Im Gegensatz zu !(TRUE | TRUE).-, daher ist das Ergebnis -25.Markieren sie die wahren Aussagen!
! bindet stärker als das ODER !, daher ist der Ausdruck TRUE - Im Gegensatz zu !(TRUE | TRUE).-, daher ist das Ergebnis -25.%/% bindet stärker als /
Markieren sie die wahren Aussagen!
%/% bindet stärker als /
! bindet stärker als das ODER !, daher ist der Ausdruck TRUE - Im Gegensatz zu !(TRUE | TRUE).-, daher ist das Ergebnis -25.-2*-2.Markieren sie die wahren Aussagen!
- bindet stärker als Multiplakation und Division.2^3^2 = 2^(3^2).Markieren sie die wahren Aussagen!
! bindet stärker als das ODER !, daher ist der Ausdruck TRUE - Im Gegensatz zu !(TRUE | TRUE).! ist das logische NICHT, das nur ein Argument hat. Der Operator wird von links nach rechts ausgewertet.Markieren sie die wahren Aussagen!
! bindet stärker als das ODER !, daher ist der Ausdruck TRUE - Im Gegensatz zu !(TRUE | TRUE).- bindet stärker als Multiplakation und Division.<- bindet stärker als =. Das heißt während in die Zuweisungen a = b <- 2 beiden Objekten die 2 zugeordnet ist, liefert a <- b = 2 einen Fehler.Markieren sie die wahren Aussagen!
-, daher ist das Ergebnis -25.! bindet stärker als das ODER !, daher ist der Ausdruck TRUE - Im Gegensatz zu !(TRUE | TRUE).-2*-2.-10:-1 sind sinnvoll definiert.Markieren sie die wahren Aussagen!
-10:-1 sind sinnvoll definiert.%/% bindet stärker als /
- bindet stärker als Multiplakation und Division.%>% bzw. auch die native Pipe |> binden genau so stark wie alle %-Operatoren.Markieren sie die wahren Aussagen!
1 bis 5 in Schritten von 1 erzeugt.%/% bindet stärker als /
<- bindet sehr schwach nur = und ? binden noch schwächer.Die gewöhnlichen mathematischen Funktionen und auch sehr viele statistische Funktionen sind in R bereits definiert. Der Aufruf erfolgt durch den Namen der Funktion gefolgt von einem Paar runden Klammern in dem das Argument bzw. die Argumente stehen.
sqrt(16) # Quadratwurzel von 16[1] 4exp(1) # Exponentialfunktion an der 1 ausgewertet[1] 2.718282log(16) # Logarithmus von 16 zur Basis e[1] 2.772589log(16, base = 2) # Logarithmus von 16 zur Basis 2[1] 4sin(pi/2) # Sinus von π/2, wobei π die Kreiszahl 3.1415926... ist [1] 1Bei allen Funktionen ist auf die korrekte Schreibweise zu achten, insbesondere macht Groß- und Kleinschreibung einen Unterschied: R ist case-sensitive. Wenn also eine Funktion falsch geschrieben ist, meldet R einen Fehler zurück.
Sqrt(16) # liefert Fehler, da Funktion nicht existiertError in Sqrt(16): konnte Funktion "Sqrt" nicht findenchoose() muss sowohl das n als auch das k angegeben werden und bei round() ist der Standard, dass auf ganze Zahlen gerundet wird.
| Funktion | Bedeutung |
|---|---|
abs() / sign()
|
Betragsfunktion / Algebraisches Vorzeichen |
sqrt() |
Quadratwurzel |
sin() / cos() / tan()
|
Trigonometrische Funktionen |
asin() / acos() / atan() / atan2()
|
Arkusfunktionen (Umkehrfunktionen) |
exp() |
Exponentialfunktion \textsf{e}^x |
log() / log10() / log2()
|
Logarithmus zur Basis \textsf{e} / 10 / 2 |
sinh() / cosh() / tanh()
|
Hyperbolische Funktionen |
asinh() / acosh() / atanh()
|
Areafunktionen (Umkehrfunktionen) |
factorial() |
Fakultät (eigentlich: \Gamma(x+1)) |
choose(n, k) |
Binomialkoeffizient: n über k : \binom{n}{k}
|
round(x, digits = 0) |
Rundet x auf 0 Stellen nach dem Komma |
signif(x, digits = 6) |
Rundet x auf 6 signifikante Stellen |
floor() / ceiling()
|
Abrunden / Aufrunden |
sum() / prod()
|
Summe / Produkt der Elemente eines Vektors |
R hat einige vordefinierte Konstanten und Sonderwerte (im weitesten Sinne), die man zum Rechnen nutzen kann, oder aber die bei Rechnungen als Ergebnis herauskommen können.
| Konstante | Bedeutung |
|---|---|
pi |
Mathematische Konstante \pi |
| Sonderwerte | Bedeutung |
|---|---|
Inf / -Inf
|
\infty / -\infty |
NA |
Fehlender Wert (Not Available) |
NaN |
Keine Zahl (Not a Number) |
NULL |
Leere Menge |
NaN, wenn eine Rechnung zum Beispiel keine reelle Zahl als Lösung hat.log(-1)Warning in log(-1): NaNs wurden erzeugt[1] NaN# Bemerkung: mit komplexen Zahlen ginge es...
log(-1+0i)[1] 0+3.141593iInf bzw. -Inf nicht notwendigerweise wirklich unendlich: auch sehr große Zahlen werden als unendlich behandelt:log(0) [1] -Inffactorial(171) [1] Inffactorial(170) # letzte Fakultät, die noch als endliche Zahl dargestellt wird![1] 7.257416e+306Das e in der obigen Schreibweise der Zahl steht für Exponent und gibt die Zehnerpotenz der darzustellenden Zahl an. So ist 6.022e+23 das gleiche wie 6.022\cdot 10^{23} und analog 6.626e-34 das gleiche wie 6.626\cdot 10^{-34}. Man bezeichnet diese Schreibweise als wissenschaftliche Notation, die insbesondere bei großen bzw. Zahlen nahe der Null angewendet wird. Natürlich werden Zahlen in R nicht nur so ausgegeben, sondern können auch derart eingegeben werden.
2.1e1[1] 213.2e-1[1] 0.32In R sind alle Funktionen auch Objekte. Der Aufruf der Funktionen ist dabei im wesentlichen immer der gleiche:
name_der_funktion(arg1 = wert1, arg2 = wert2, arg3 = wert3)Hinter dem Namen der Funktion steht ein Paar Runde Klammern und in dieser werden die Argumente der Funktion aufgerufen. Dabei ist zu beachten, dass es Argumente gibt, die zwingend angegeben werden müssen und Argumente, die optional sind bzw. einen vordefinierten Wert annehmen, wenn man das Argument nicht angibt.
log()
Schauen wir uns die Funktion log() einmal genauer an. Gibt man den Funktionsnamen ohne die runden Klammern ein, so wird nur der Quellcode ausgegeben.
logfunction (x, base = exp(1)) .Primitive("log")Wir sehen an diesem Beispiel, dass die Funktion log() zwei Argumente hat:
x ist das erste Argument und es ist ein notwendiges Argument, da ihm kein Wert zugeordnet ist.base ist das zweite Argument, allerdings hat base den vordefinierten Wert exp(1) (also die Euler-Konstante \textsf{e})Außerdem können wir am Ausdruck .Primitive() sehen, dass die Funktion nicht in R sondern in einer anderen, schnelleren Programmiersprache programmiert ist, was uns an der Stelle aber egal ist. Andere Funktionen können an der Stelle einen länglichen R-Code liefern.
log() # liefert Fehler, da x nicht angegebenError in log(): Argument "x" fehlt (ohne Standardwert)log(x=16) # ok, hier: x = 16, base = exp(1)[1] 2.772589log(x=16, base=2) # base ist optional, hier Basis 2[1] 4log(16, 2) # ist das gleiche wie vorheriges Beispiel [1] 4Die Reihenfolge in der Argumente angegeben werden (müssen) ist wichtig, wenn die Argumentnamen nicht angegeben werden! Das erste Argument, das angegeben wird, wird dem ersten Argument der Funktion übergeben. Im obigen Beispiel ist das die 16, die dem Argument x= übergeben wird. Das zweite Argument wird dem zweiten Argumentnamen übergeben und so weiter. Im obigen Beispiel ist klar, welche Bedeutung den jeweiligen Zahlen zukommen.
log(base=2, x=16) [1] 4In der Praxis ist es allerdings so, dass man bei sehr vielen Funktionen nicht alle Argumente aufrufen muss oder möchte, da sie zum Beispiel richtig vordefiniert sind. Andere Argumente stehen ggf. hinten in der Argumentliste, und wir wollen nur diese ändern. In diesen Fällen ist es unumgänglich die Namen der Argumente anzugeben!
Ein Beispiel hierfür wäre die geometrische Funktion geom_point() aus Kapitel 3 die offenbar recht viele Argumente hat.
geom_pointfunction (mapping = NULL, data = NULL, stat = "identity", position = "identity",
..., na.rm = FALSE, show.legend = NA, inherit.aes = TRUE)
{
layer(mapping = mapping, data = data, geom = "point", stat = stat,
position = position, show.legend = show.legend, inherit.aes = inherit.aes,
params = list2(na.rm = na.rm, ...))
}
<bytecode: 0x5d5410a4add0>
<environment: 0x5d5410a48970>Allein um die Übersicht zu wahren und da meist nur wenige Argumente geändert werden, schreibt man die Argumentnamen in den Funktionsaufruf.
penguins |> ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
geom_point(shape = 2)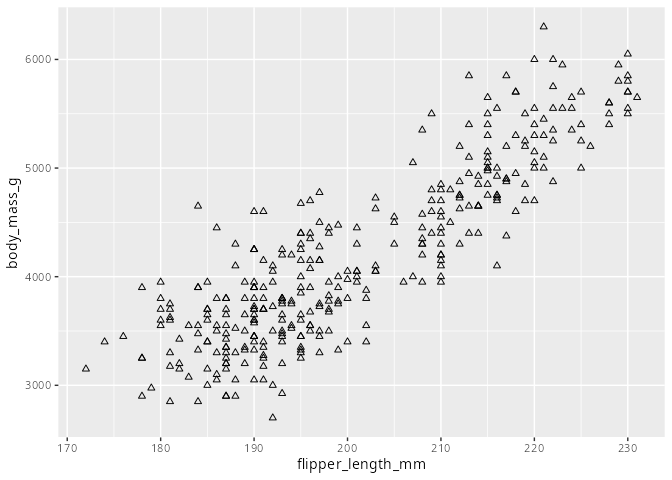
ln(16) # ln keine FunktionError in ln(16): konnte Funktion "ln" nicht findenLog(16) # Gross- / Kleinschreibung wichtigError in Log(16): konnte Funktion "Log" nicht findenlog(-1) # NaN - Not A NumberWarning in log(-1): NaNs wurden erzeugt[1] NaNDie Funktion help() ist die wichtigste Funktion von allen! Man erhält mir ihr folgende Informationen zu den Funktionen oder Operatoren:
Eine Beschreibung der Funktion kann sehr wichtig sein, da es nicht immer offensichtlich was eine Funktion wirklich macht, welche Ausgabe die Funktion hat und so weiter. Die Syntax ist für das Aufrufen der Funktion von großer Wichtigkeit, da die Namen und die Reihenfolge der Argumente nicht offensichtlich sind. Zudem ist meist auch nicht klar, welche Argumente (und damit welche Funktionalitäten) überhaupt zur Verfügung stehen. Insbesondere bei komplizierten Funktionen sind Beispiele sehr hilfreich um mit den Funktionen warm zu werden und sie richtig und geeignet anzuwenden.
oder die kurze Variante:
?"["
?"%*%"
?plotZu beachten ist an den oberen Beispielen, dass
Die wichtigste Struktur von R sind Vektoren. Eine einfache Variante um Vektoren zu erstellen ist die Funktion c(), was für concatenate (verknüpfen, aneinanderhängen), combine (verbinde, vereinen) oder coerce (zwingen) steht. Letzteres mag überraschen wird aber im Laufe des Kapitels noch klar werden. Alle Elemente eines Vektors haben immer den gleichen Datentyp, zum Beispiel Zeichen(ketten) (character), Zahlen (numeric) oder logische Ausdrücke (logical).
[1] 3 14 15 9 2 6wahrheitswerte <- c(TRUE, FALSE, TRUE)Da mit c() Vektoren verknüpft werden, können damit verschiedene Vektoren zusammengfügt werden, zum Beispiel
ist x_neu ein numerischer Vektor, der sieben Elemente enthält.
Logische Vektoren enthalten nur TRUE, FALSE oder NA und entstehen in den meisten Fällen durch Vergleiche.
(alter <- c(17, 16, 21, 20, 19, 17, 19, NA, 24, 17)) [1] 17 16 21 20 19 17 19 NA 24 17(volljaehrig <- alter >= 18) [1] FALSE FALSE TRUE TRUE TRUE FALSE TRUE NA TRUE FALSESie sind der einfachste Datentyp in R. Oft benötigt man die logischen Werte nicht direkt, sondern sie tauchen IN vERGLEICHEN implizit auf um Entscheidungen zu treffen. Beispiele dafür sind
filter() in der ein Vergleich steht: ist dieser Vergleich FALSE, so wird die Zeile herausgefiltert, erscheint also nicht in der resultierenden Datentabelle.# tidyverse muss geladen sein!
mpg |> filter(model == "corvette")# A tibble: 5 × 11
manufacturer model displ year cyl trans drv cty hwy fl class
<chr> <chr> <dbl> <int> <int> <chr> <chr> <int> <int> <chr> <chr>
1 chevrolet corvette 5.7 1999 8 manual(… r 16 26 p 2sea…
2 chevrolet corvette 5.7 1999 8 auto(l4) r 15 23 p 2sea…
3 chevrolet corvette 6.2 2008 8 manual(… r 16 26 p 2sea…
4 chevrolet corvette 6.2 2008 8 auto(s6) r 15 25 p 2sea…
5 chevrolet corvette 7 2008 8 manual(… r 15 24 p 2sea…Das Konzept des Filtern mit filter() wird in Kapitel 8.3 genauer erklärt.
Zeichenketten sind der komplexeste Datentyp in R. Zeichenketten stehen in Anführungszeichen
namen <- c("Andreas", "Berta", "Carl", "Dagmar", "Else") Im Wesentliche können alle Zeichen innerhalb einer Zeichenkette stehen, allerdings müssen manche Sonderzeichen escaped werden, da ihnen innerhalb der Programmiersprache R eine besondere Bedeutung zukommt. Eine Liste erhält man mit help('"').
Mit der Funktion paste() können Zeichenketten zusammengführt werden.
Ist es möglich Objekte verschiedener Datentypen zusammenzuführen, und wenn ja, was passiert dann? Ja, es ist möglich! Die Einträge der Vektoren werden in einen neuen Vektor gezwungen. Der so entstandene Vektor hat dann den Typ des komplexesten auftauchenden Bestandteils.
:-Operator-3:7 # Vektor in 1er Schritten [1] -3 -2 -1 0 1 2 3 4 5 6 71.3:6[1] 1.3 2.3 3.3 4.3 5.3Der :-Operator erzeugt einen auf- oder absteigenden numerischen Vektor bei dem der Startwert auf der linken Seite des Operators steht und der Endwert auf der rechten Seite. Dabei unterscheiden sich die Einträge des Vektors jeweils um 1 oder -1. Wir der Endwert nicht genau getroffen, so ist der nächst kleine Eintrag der letzte des Vektors.
seq()
Eine Erweiterung des :-Operators ist die Funktion seq() bei der beliebige Schrittgrößen möglich sind.
seq(0, 5, 0.5) # Vektor in 0.5er Schritten [1] 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0Es ist auch möglich mit Hilfe der Arguments length.out= die Länge des erzeugten Vektors festzulegen. Dabei ist die Schrittgröße konstant und wird dementsprechend berechnet.
seq(2,6, length.out = 12) # Vektor der Länge 12 (äquidistant) [1] 2.000000 2.363636 2.727273 3.090909 3.454545 3.818182 4.181818 4.545455
[9] 4.909091 5.272727 5.636364 6.000000rep()
Eine weitere praktische Funktion ist die Funktion rep() mit der Vektoren erzeugt werden können, die Wiederholungen enthalten. Dazu gibt es mehrere Möglichkeiten:
rep(1:3, 4) # Wiederholt den Vektor 1, 2, 3 viermal [1] 1 2 3 1 2 3 1 2 3 1 2 3[1] "Eins" "Zwei" "Zwei" "Viele" "Viele" "Viele" "Viele" "Viele"each= wird jedes Argument so oft wie angegeben wiederholt bevor das nächste Argument wiederholt wird.rep(1:3, each = 4) # Wiederholt 1, 2, 3 je viermal [1] 1 1 1 1 2 2 2 2 3 3 3 3Als praktische Anwendung der Funktion seq() wollen wir nun Graphen von Funktionen darstellen. Man kann R nicht einfach einen Funktionsterm geben, der dann einfach so als Grafik dargestellt wird. Statt dessen müssen wir um ggplot2 zu nutzen eine Datentabelle erzeugen, die x- und die y-Koordinaten enthält. Diese Koordinaten werden dann verbunden. Dies ist ziemlich analog dazu, wie man es händisch auf einem Blatt Papier machen würde.
Als Beispiel wollen wir eine Normalparabel y = x^2 im Intervall [-2, 2] darstellen. Einen solchen Datentabelle kann man mit der Funktion tibble() generieren.
parabel1 |> ggplot(aes(x=x, y=y)) +
geom_line(linewidth = 1.2) 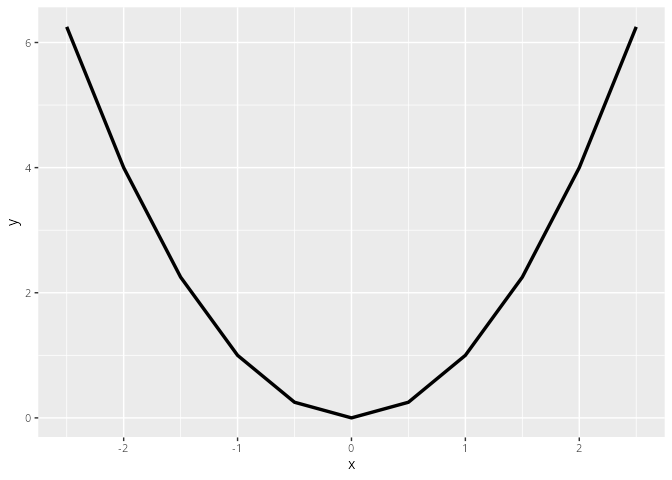
geom_line() verbindet die Punkte miteinander, wobei die vorkommenden Werte der x-Achse sortiert werden. Die Datenpunkte sind hier aber zu weit auseinander, daher sieht die Parabel nicht glatt aus, sondern ist nur ein Polygonzug.
parabel2 |> ggplot(aes(x=x, y=y)) +
geom_line(linewidth = 1.2) 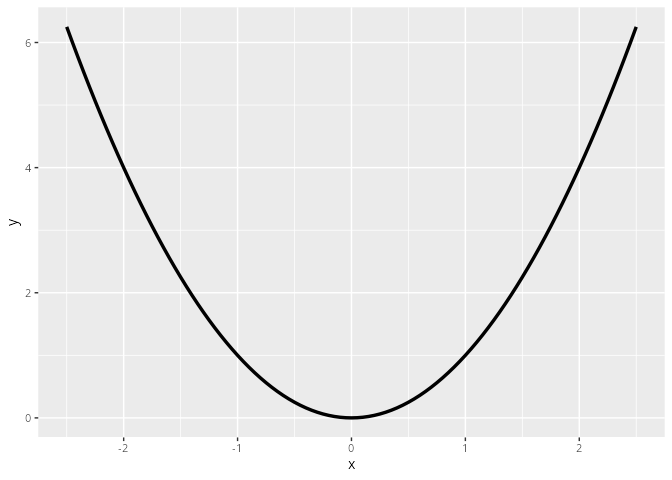
Ein sehr praktisches Konzept im Umgang mit Vektoren ist das Recycling. Beim Recycling werden Vektoren (ggf. nur Teile von Vektoren) wiederverwendet, so dass Vektoren ungleicher Länge verrechnet oder verglichen werden können.
ist damit das Gleiche wie
6 ist kein Vielfaches von 4, daher Warnung
1:6 + c(1,10,100,1000) Warning in 1:6 + c(1, 10, 100, 1000): Länge des längeren Objektes
ist kein Vielfaches der Länge des kürzeren Objektes[1] 2 12 103 1004 6 16geht auch bei Vergleichen (später dazu mehr) 4 wird mit jedem Vektoreintrag verglichen
4 > 3:6[1] TRUE FALSE FALSE FALSEEs gibt ein paar Vektoren, die bereits vordefiniert sind.
| Vektorname | Bedeutung |
|---|---|
pi |
Kreiszahl \pi |
letters |
Kleinbuchstaben |
LETTERS |
Großbuchstaben |
month.name |
Monatsnamen |
month.abb |
Monatsnamen (nur 3 Buchstaben) |
Es gibt viele Situationen in denen es sinnvoll ist auf einzelne Elemete oder eine Gruppe von Elementen eines Vektors zuzugreifen. Dies geschieht mit dem mit den eckigen Klammern [] direkt im Anschluss an den Vektor. Dabei gibt es mehere Methoden wie die Auswahl der Elemente erfolgen kann.
Als Beispiel schauen wir uns den folgenden Vektor an:
Schreibt man in die eckigen Klammern einen positiven, ganzzahligen Vektor, so werden diese Elemente ausgewählt:
vornamen[c(1,4,5)][1] "Alex" "Doro" NA Es ist auch möglich Einträge zu wiederholen (auch wenn dies in der Praxis nahezu nie vorkommt):
vornamen[rep(3:4, times = 3)][1] "Carl" "Doro" "Carl" "Doro" "Carl" "Doro"Schreibt man einen negativen, ganzzahligen Vektor (oder einen positiven mit einem - davor), so werden diese Elemente ausgelassen:
vornamen[-c(1,4,5)][1] NA "Carl" "Frank" "Gerd" "Hugo" Es ist natürlich nicht möglich, positive und negative Werte in dem Auswahlvektor zu kombinieren.
Am häufigsten verwendet man die Auswahl der Einträge über einen logischen Ausdruck. Schauen wir uns dazu ein paar Beispiele an:
zahlen[zahlen < 15][1] 11 12 13 14Um zu verstehen, was hier genau passiert, müssen wir uns klar machen, was im inneren der Klammer passiert: Der Ausdruck
zahlen < 15[1] TRUE TRUE TRUE TRUE FALSE FALSE FALSE FALSEist also ein Vektor, der nur aus den Wahrheitwerten TRUE und FALSE, sowie ggf. NAs besteht. Der logische Vektor hat genau die Länge des Vektors x. Im Ausdruck x[x<15] werden nun alle Elemente ausgewählt bei denen der Ausdruck TRUE oder NA ist, wobei zu bemerken ist, dass die Ausgabe für die NAs immer auch ein NA ist, wie das folgende Beispiel zeigt:
y <- 1:3
y[c(FALSE, NA, TRUE)][1] NA 3Man kann auch alle Nicht-NA-Einträge eines Vektors herausfiltern. Dazu benötigt man die Funktion is.na(), beziehungsweise deren Verneinung.
zahlen_mit_na[!is.na(zahlen_mit_na)][1] 11 12 14 16 17 18Der Pipe-Operator |> (oder %>% aus Paket magrittr / Tidyverse) ermöglicht eine sehr intuitive Syntax, die insbesondere mit den Tidyverse-Befehlen aber auch für R-Base Funktionen praktisch ist.
Was links vom Operator |> steht, wird als erstes Argument in der Funktion rechts des Operators verwendet.
Formal entspricht x |> f() (auch: x %>% f() also dem Aufruf f(x). Alle weiteren Argumente können der Funktion auf die übliche Weise hinzugefügt werden, wie man am Beispiel sehen kann. Aus dem Funktionsaufruf f(x, y) wird formal mit der Pipe x |> f(y)
Das Ergebnis kann dann wiederum mit der Pipe |> in eine nächste Funktion geschoben werden, und so weiter. Der große Vorteil liegt darin, dass unübersichtliche Verschachtelungen zu einer linearer Abfolge (von innen nach außen) werden.
Im ersten Beispiel soll der folgende geschachtelte Ausdruck mittels Pipe-Operator ausgeführt werden:
Dieser Ausdruck wird von innen nach außen ausgeführt, das heißt zuerst wird der Logarithmus von 2.44 zur Basis 3 berechnet, dann auf zwei Nachkommastellen gerundet und aus dem Ergebnis zieht man die Quadratwurzel.
Verwendet man den Pipe-Operator, so vereinfacht sich die letzte Formel zu
Man fängt mit der innersten Klammer an 2.44. Den Ausdruck schiebt man in die Funktion log(), wobei base=3 das zweite Argument der Funktion ist. Das Ergebnis aus der Rechnung wird in die Funktion round() geschoben. Diese Funktion round() hat als erstes Argument x dem das Ergebnis aus der Pipe zugewiesen wird. Das zweite Argument der Funktion round() ist digits=0. Möchte man das zweite Argument ändern so muss man dies angeben (siehe oben). Da es sich um das zweite Argument in der Funktion handelt, kann der Argumentname auch unterdrückt werden:
Das Ergbnis aus dieser Rechnung wird dann in die letzte, das heißt äußerste Funktion geleitet.
Das zweite Beispiel ist aus dem Tidyverse: es kommt bei der Datenverarbeitung oft vor, dass Daten aufgearbeitet werden. So werden in Datentabellen Zeilen gefiltert, Spalten ausgewählt oder neu erzeugt, Kenngrößen berechnet, Grafiken erzeugt und vieles mehr. Bei diesen Prozessen ist es üblich, dass Daten bearbeitet werden und mit diesen dann weiter gearbeitet wird. Hierfür eignet sich der Pipe-Operator besonders gut.
Im Beispiel unten sind nur zwei Schritte zu sehen (filtern und danach eine Grafik erzeugen). Man kann hier noch einen großen Vorteil in der Pipe-Schreibweise erkennen: soll auf das Filtern verzichtet werden, so kann diese Zeile einfach mit einem # auskommentiert werden. Der restliche R-Code läuft dann trotzdem. Im Fall ohne Pipe ist der Schritt deutlich umständlicher und sehr viel fehleranfälliger.