13  Aufbau einer Grafik

In diesem Kapitel werden wir anhand mehrerer interessanter Datensätze den Aufbau einer ggplot2-Grafik vertiefen. Für den ersten Teil nutzen wir die Datentabelle mpg, die im ggplot2 Paket enthalten ist.

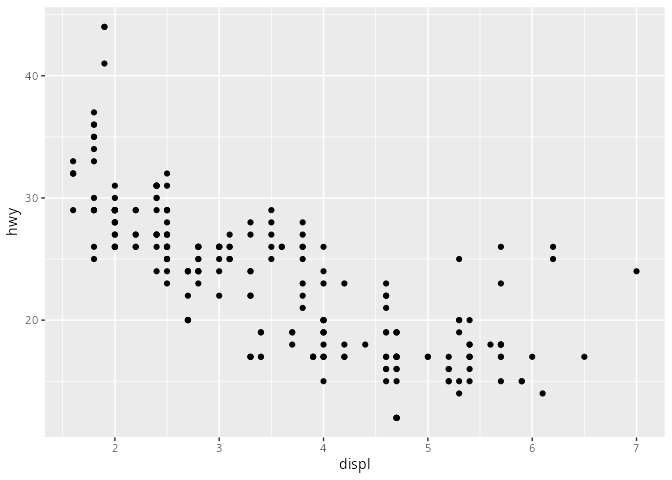
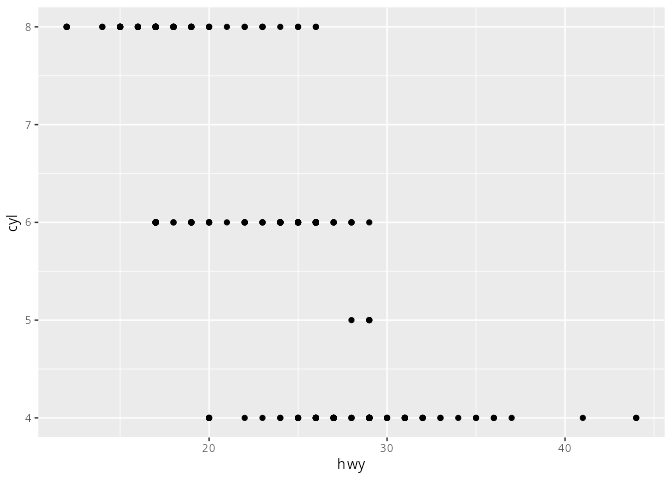
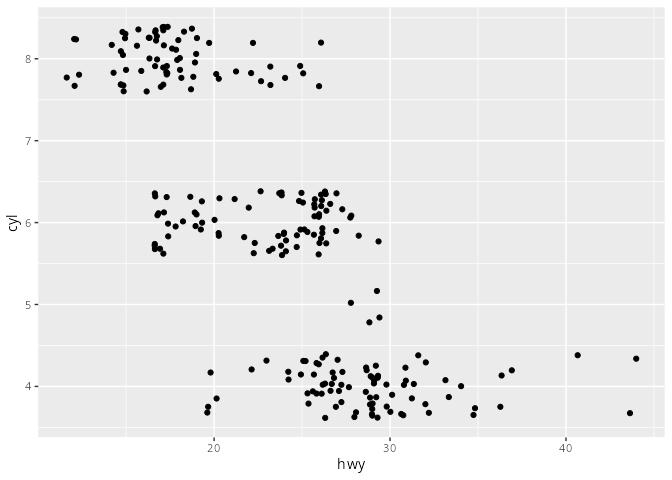
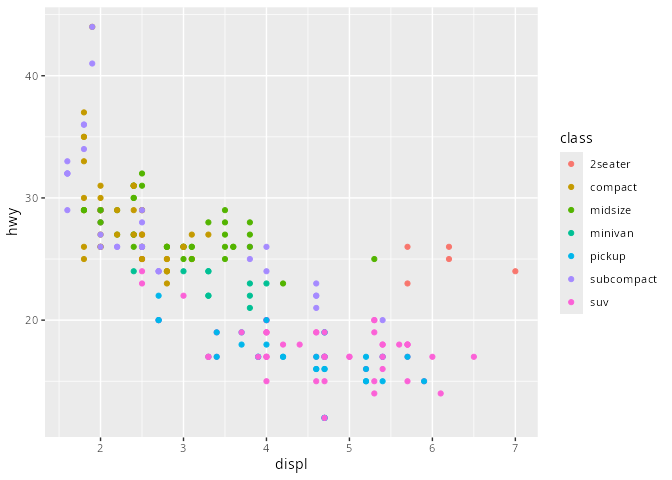
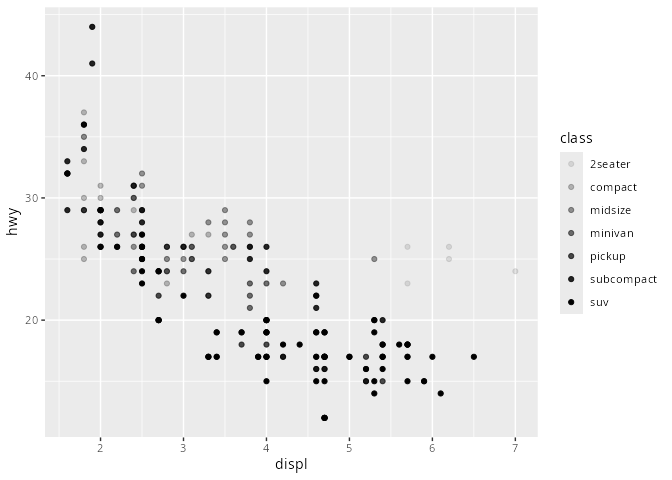
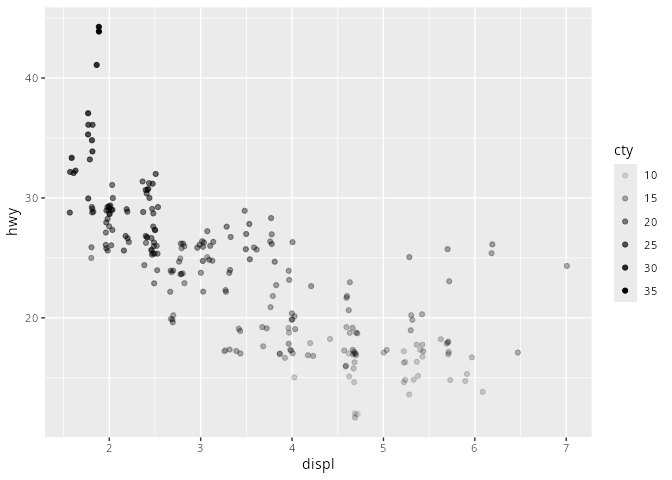
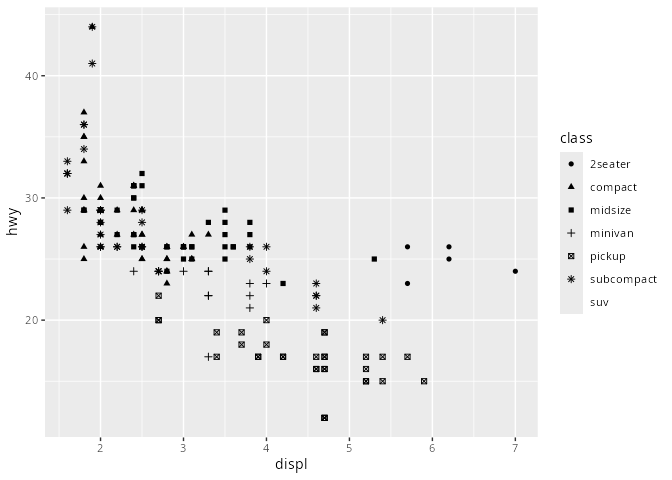
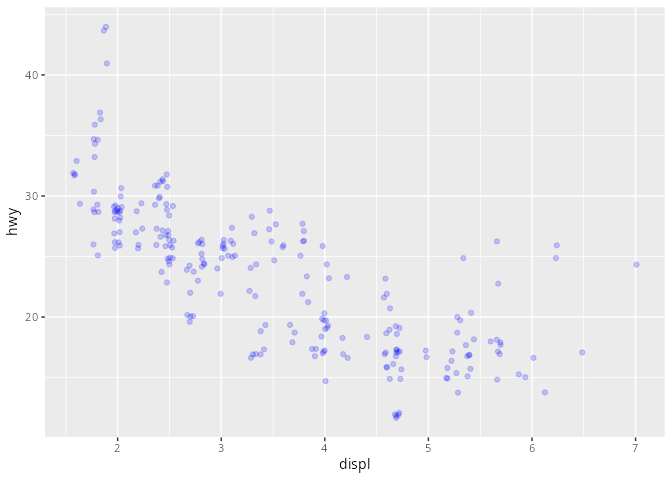
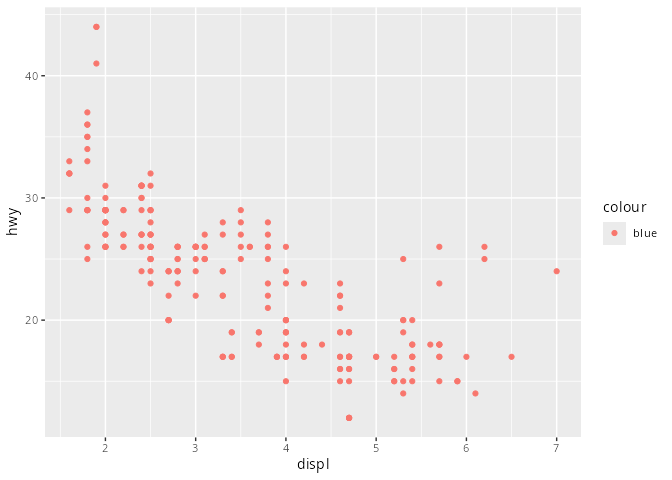
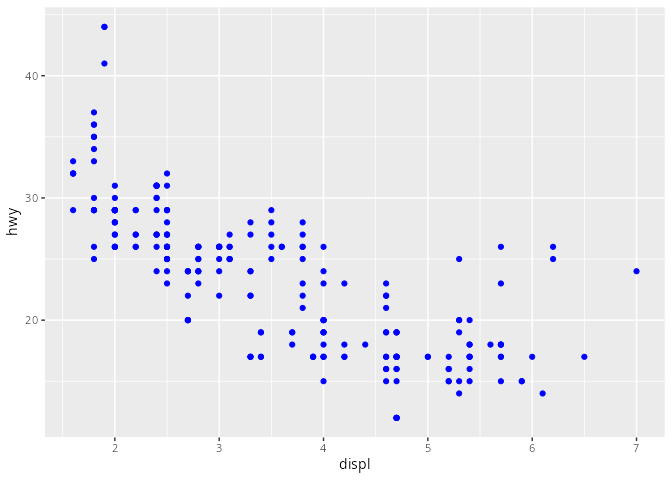
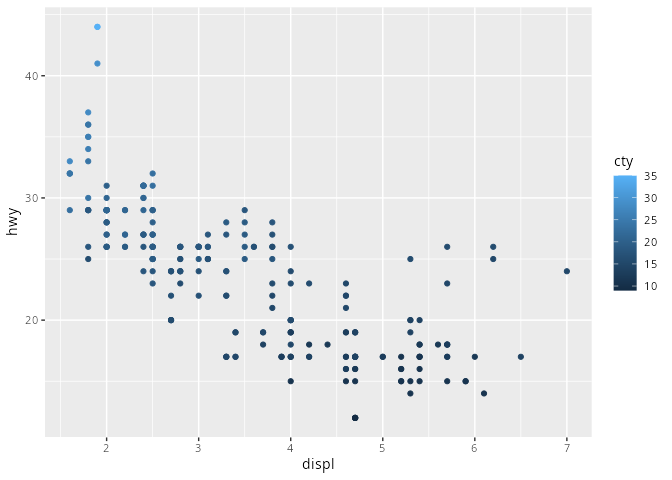
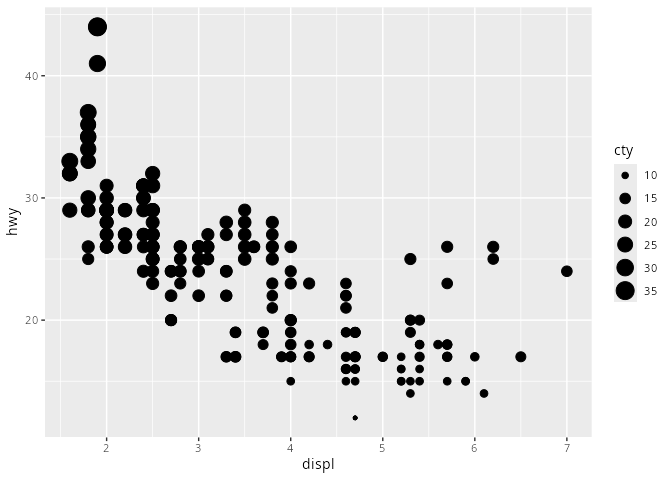
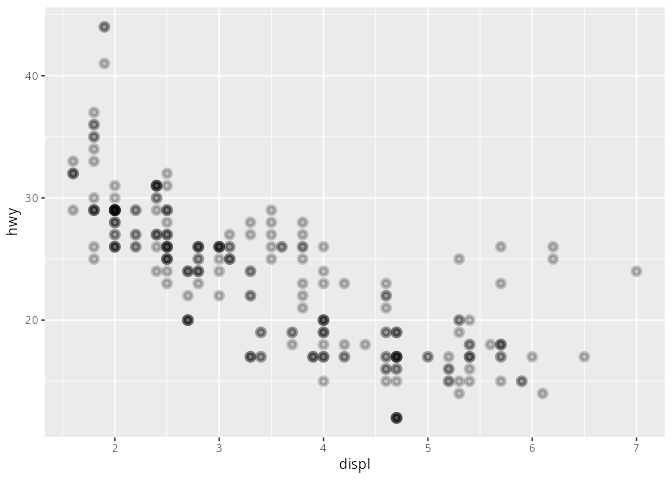
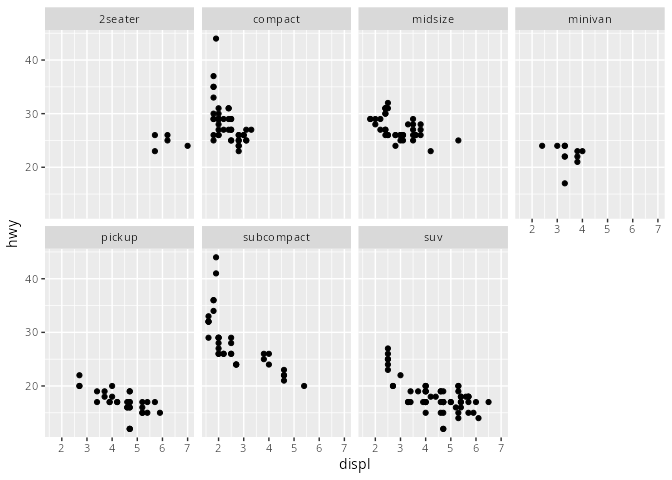
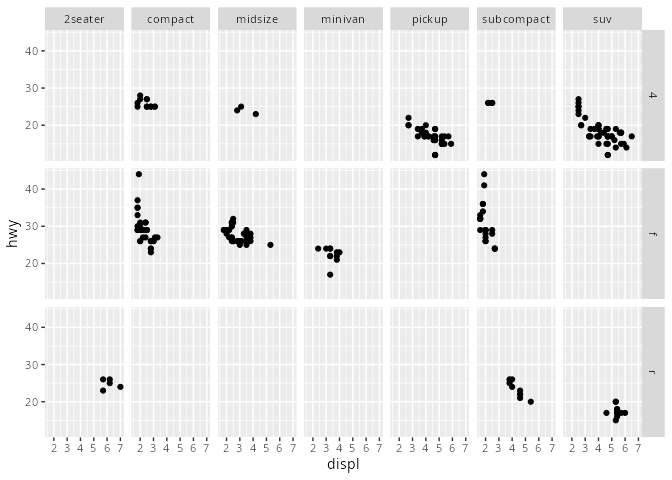
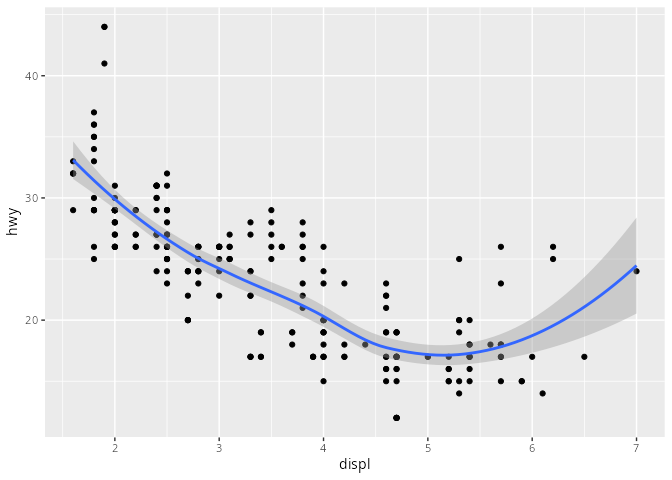
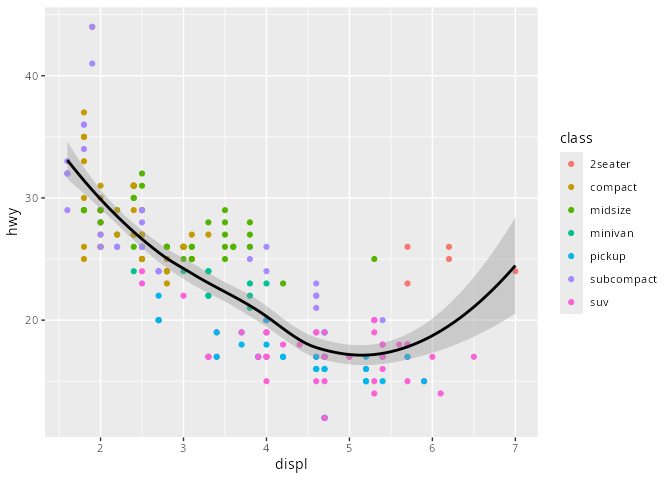
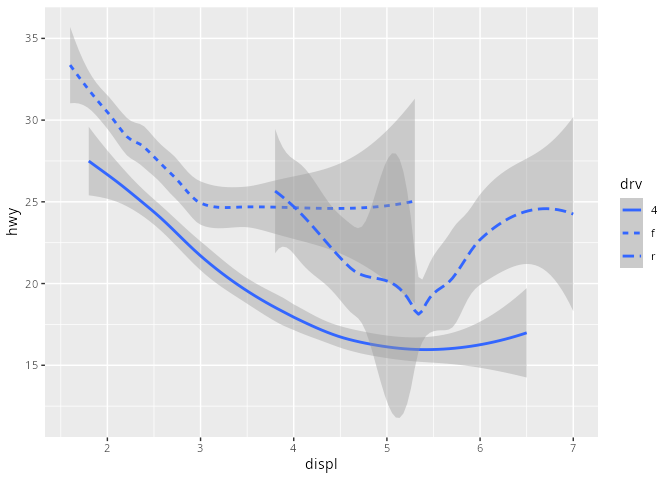
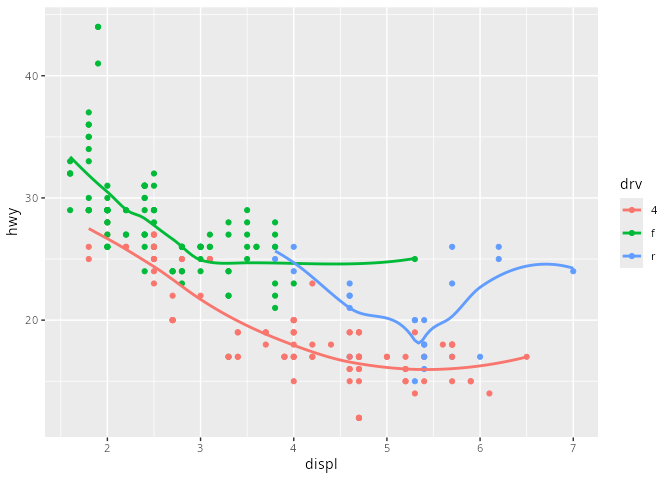
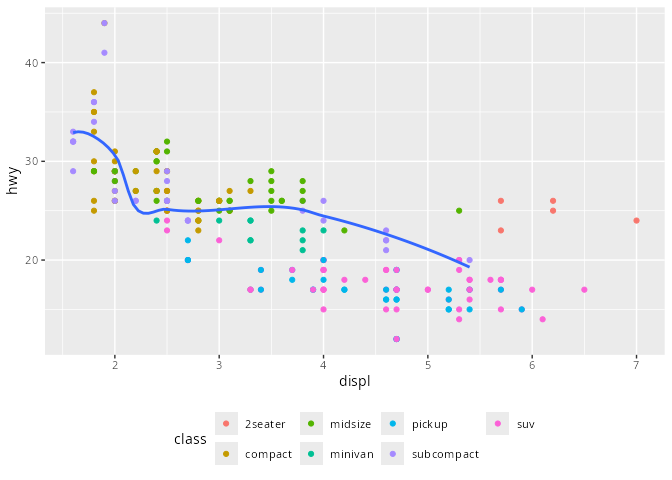
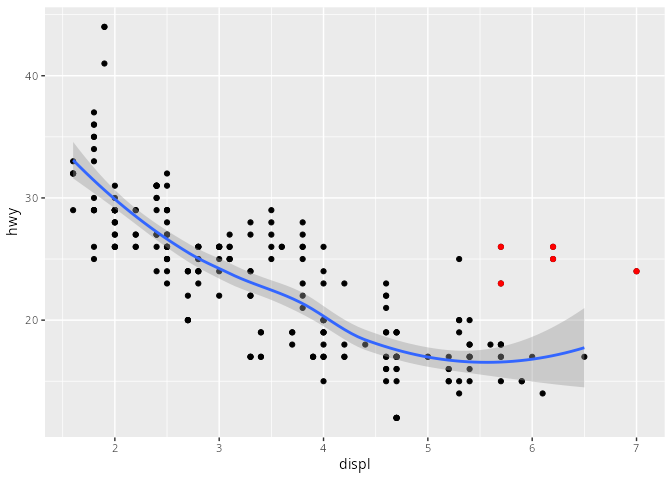
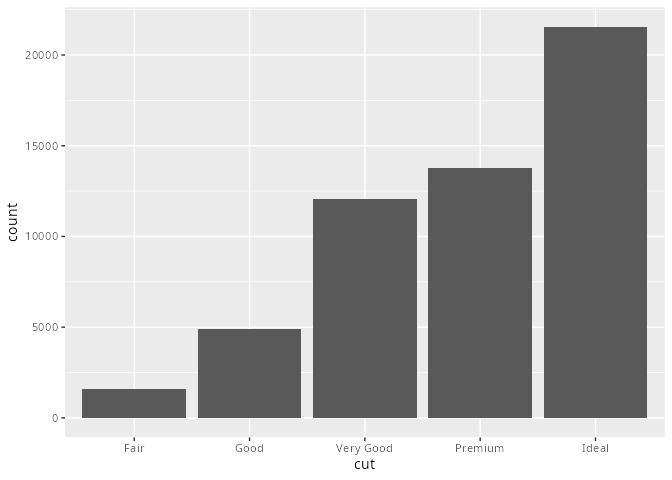
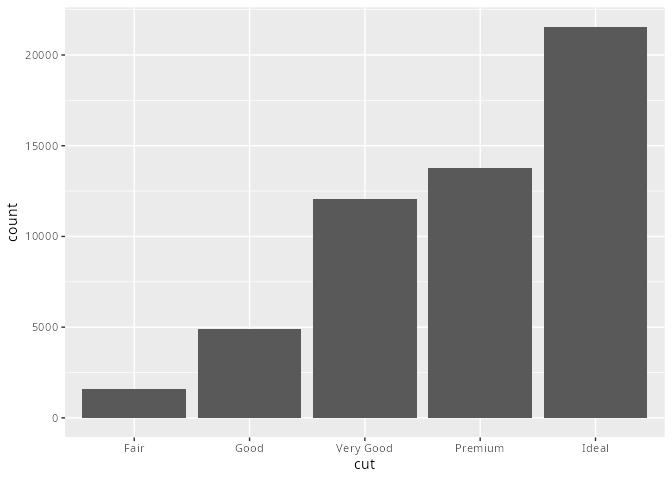
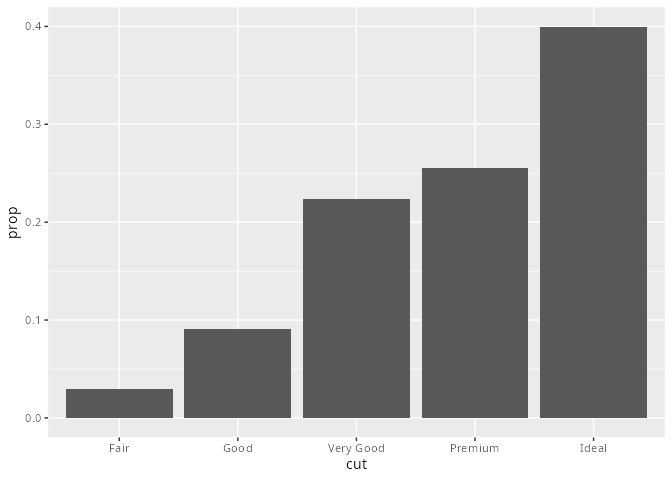
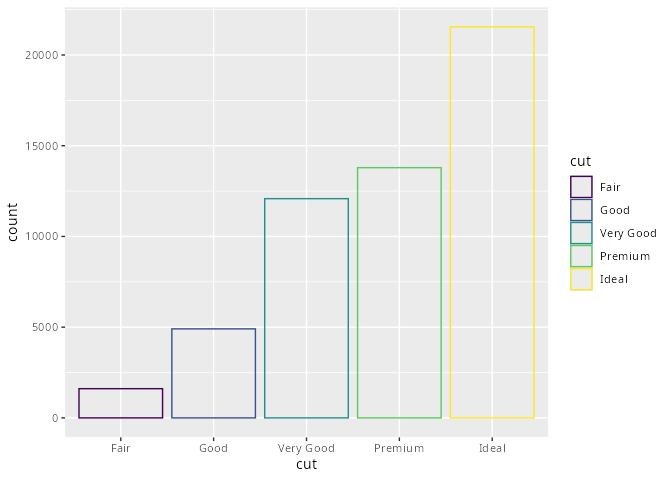
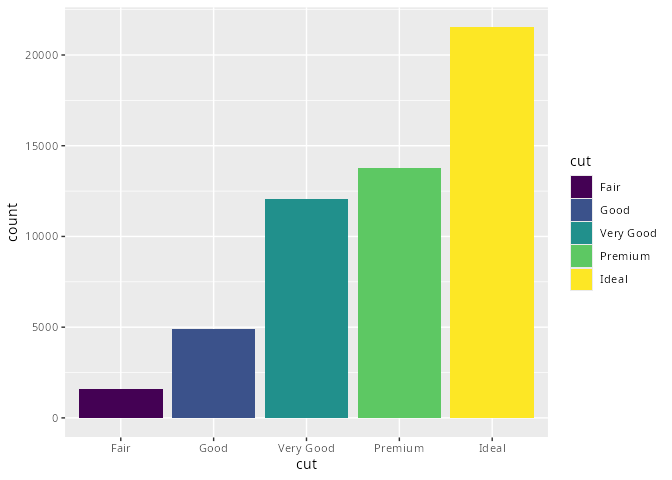
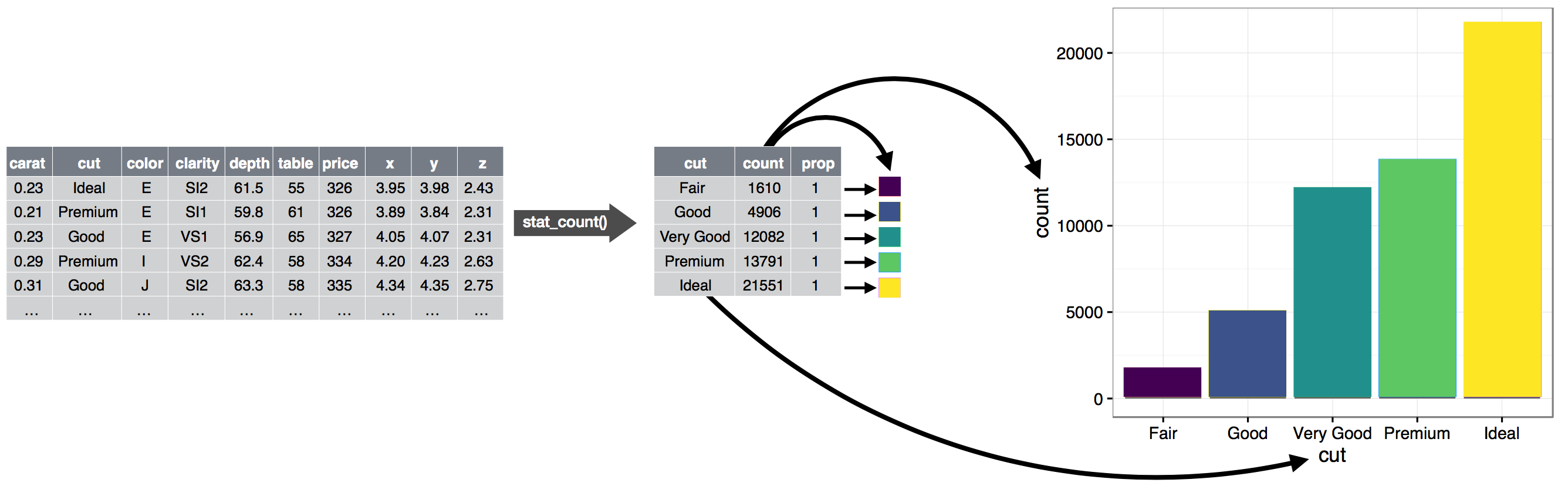
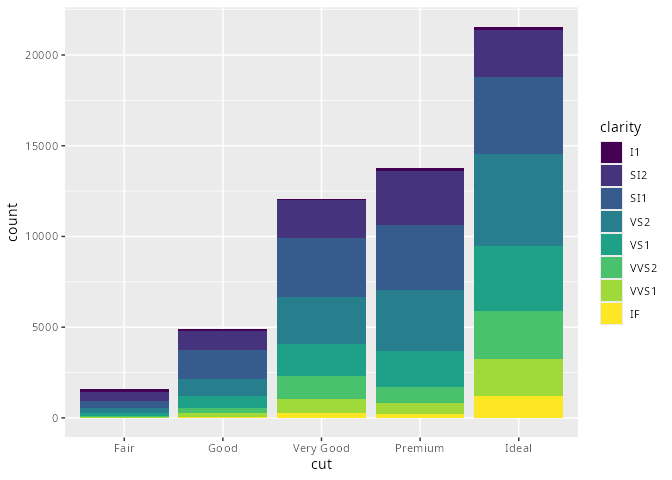
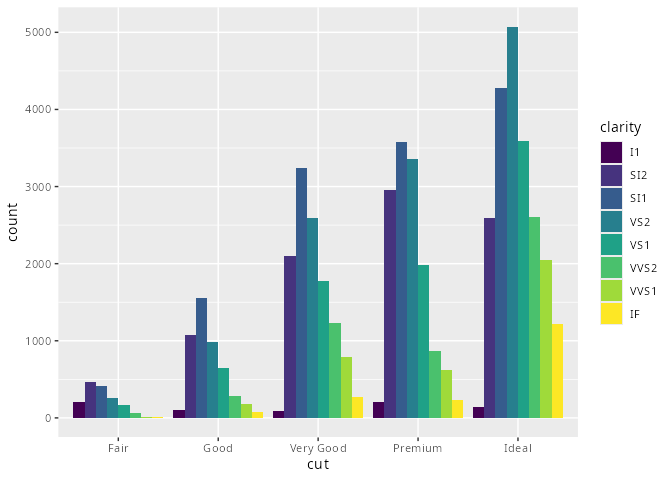
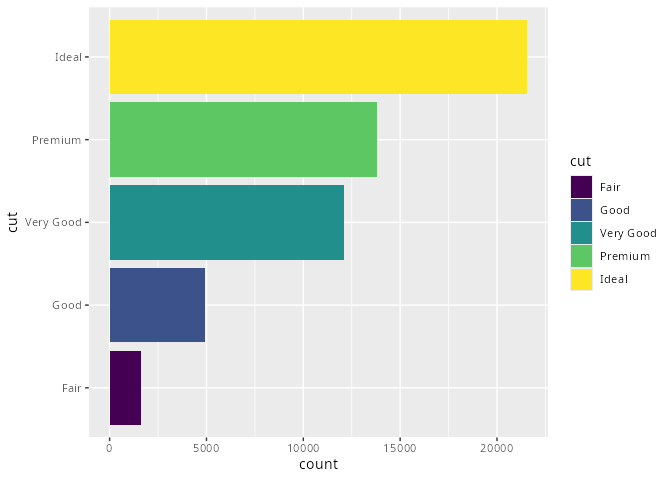
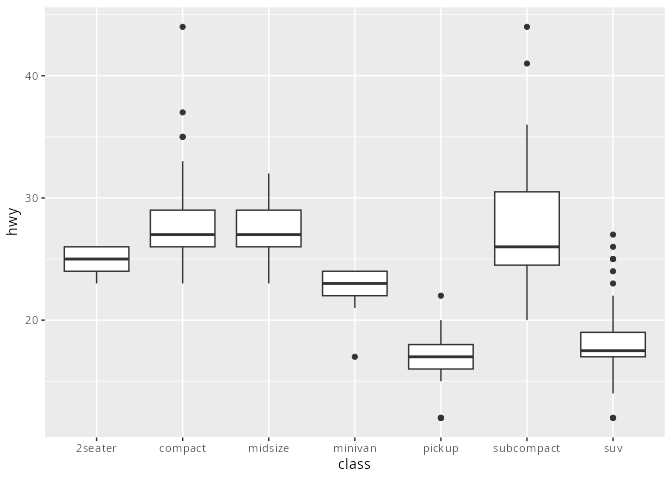
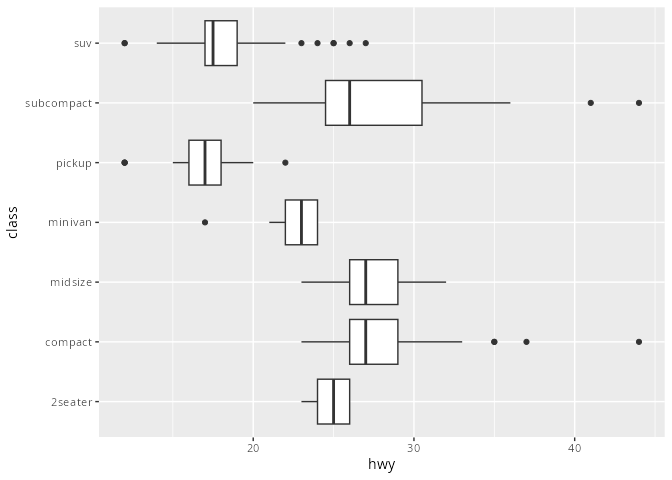
mpg
# A tibble: 234 × 11
   manufacturer model      displ  year   cyl trans drv     cty   hwy fl    class
   <chr>        <chr>      <dbl> <int> <int> <chr> <chr> <int> <int> <chr> <chr>
 1 audi         a4           1.8  1999     4 auto… f        18    29 p     comp…
 2 audi         a4           1.8  1999     4 manu… f        21    29 p     comp…
 3 audi         a4           2    2008     4 manu… f        20    31 p     comp…
 4 audi         a4           2    2008     4 auto… f        21    30 p     comp…
 5 audi         a4           2.8  1999     6 auto… f        16    26 p     comp…
 6 audi         a4           2.8  1999     6 manu… f        18    26 p     comp…
 7 audi         a4           3.1  2008     6 auto… f        18    27 p     comp…
 8 audi         a4 quattro   1.8  1999     4 manu… 4        18    26 p     comp…
 9 audi         a4 quattro   1.8  1999     4 auto… 4        16    25 p     comp…
10 audi         a4 quattro   2    2008     4 manu… 4        20    28 p     comp…
# ℹ 224 more rows
glimpse(mpg)
Rows: 234
Columns: 11
$ manufacturer <chr> "audi", "audi", "audi", "audi", "audi", "audi", "audi", "…
$ model        <chr> "a4", "a4", "a4", "a4", "a4", "a4", "a4", "a4 quattro", "…
$ displ        <dbl> 1.8, 1.8, 2.0, 2.0, 2.8, 2.8, 3.1, 1.8, 1.8, 2.0, 2.0, 2.…
$ year         <int> 1999, 1999, 2008, 2008, 1999, 1999, 2008, 1999, 1999, 200…
$ cyl          <int> 4, 4, 4, 4, 6, 6, 6, 4, 4, 4, 4, 6, 6, 6, 6, 6, 6, 8, 8, …
$ trans        <chr> "auto(l5)", "manual(m5)", "manual(m6)", "auto(av)", "auto…
$ drv          <chr> "f", "f", "f", "f", "f", "f", "f", "4", "4", "4", "4", "4…
$ cty          <int> 18, 21, 20, 21, 16, 18, 18, 18, 16, 20, 19, 15, 17, 17, 1…
$ hwy          <int> 29, 29, 31, 30, 26, 26, 27, 26, 25, 28, 27, 25, 25, 25, 2…
$ fl           <chr> "p", "p", "p", "p", "p", "p", "p", "p", "p", "p", "p", "p…
$ class        <chr> "compact", "compact", "compact", "compact", "compact", "c…

Der Datensatz enthält 11 Merkmale (in den Spalten) von 234 Beobachtungen (Autos, in den Zeilen).

Tabelle 13.1: Zusammenfassung Merkmale der Datentabelle mpg.
Merkmal Bedeutung Skalentyp in R
manufacturer Hersteller nominal <chr>
model Modell nominal <chr>
displ Hubraum in Liter metrisch <dbl>
year Baujahr metrisch <int>
cyl Anzahl der Zylinder metrisch <int>
trans Getriebeart nominal <chr>
drv Antrieb nominal <chr>
cty Meilen pro Gallone in der Stadt metrisch <int>
hwy Meilen pro Gallone auf dem Highway metrisch <int>
fl Kraftstoffart nominal <chr>
class Fahrzeugklasse nominal <chr>

13.1 Schema einer Grafik

Wir wollen anhand der obigen Datentabelle die folgende Frage beantworten:

Frage: ,,Fahren Autos mit großem Motor mit einer Gallone weniger weit?’’

Sowohl das Merkmal displ als auch hwy sind metrische Merkmale. Wir haben in Kapitel 3 bereits ein Streudiagramm erstellt, was naheliegende Darstellung für die gleichzeitige Darstellung zweier metrischer Merkmale ist (siehe hierzu auch Kapitel 16.5.3).

mpg |> ggplot() +
       geom_point(aes(x = displ, y = hwy))
Abbildung 13.1: Ein einfaches Streudiagramm.

Ausgehend von einer einfachen Grafik, die nur aus der Funktion ggplot() sowie einer geometrischen Funktion (im obigen Beispiel: geom_point()) besteht, wollen wir eine allgemeine Vorlage für eine Grafik angeben. Wie bereits erwähnt sind ggplot2-Grafiken in Schichten aufgebaut. Eine Vorlage könnte zum Beispiel so aussehen:

DATEN |> ggplot() + 
         geom_FUNKTION(
            mapping = aes(MAPPING),
            stat = STAT, 
            position = POSITION,
            ...) +
         coordinate_FUNKTION() +
         facet_FUNKTION() + 
         scale_FUNKTION() +
         theme_FUNKTION() +
         labs()

wobei die groß geschriebenen Ausdrücke Platzhalter sind. Das einfachste Beispiel einer sinnvollen Grafik enthält zumindest die Funktion ggplot() sowie eine geometrische Funktion

mpg |> ggplot() +
       geom_point(aes(x = hwy, y = cyl))
Abbildung 13.2: Ein einfaches Streudiagramm. An dieser Stelle ist diese Grafik nicht gut geeignet, weil zu viele Beobachtung übereinander liegen.

Diese Grafik ist offenbar keine gute Grafik, da sehr viele Beobachtungen übereinanderliegen. Es gibt nun diverse Möglichkeiten dies zu verbessern. Eine Möglichkeit könnte sein die geometrische Funktion derart zu ändern, dass die Daten besser sichtbar werden.

mpg |> ggplot() +
       geom_jitter(aes(x = hwy, y = cyl))
Abbildung 13.3: Die gleichen Daten, aber eine andere geometrische Funktion. Die geometrische Funktion geom_jitter() wackelt ein wenig an den Koordinaten der Punkte, so dass Datenpunkte, die übereinander liegen, sichtbar werden.

Auch diese Grafik ist natürlich nicht ideal, allerdings sieht man nun schon, dass es sich um sehr viel mehr Beobachtungen handelt als Abbildung 13.2 vermuten ließ.

Aufgabe: Optimierung

Die Funktion geom_jitter() hat die Argumente width= und height=. Welche Auswirkungen hat das Ändern dieser Werte auf die Abbildung 13.3?

Wir wollen nun ein wenig systematischer an das Erstellen einer Grafik herangehen und und die Bedeutung der Aesthetics einer Grafik klarmachen.

13.2 Aesthetics

mpg |> ggplot() + 
       geom_point(aes(x = displ, y = hwy, color = class))
Abbildung 13.4: Um das kardinale Merkmal class sichtbar zu machen, wird dieses dem Argument color= zugewiesen. Die Punkte werden bezüglich der verschiedenen Ausprägungen des Merkmals class gefärbt. 
mpg |> ggplot() + 
       geom_point(aes(x = displ, y = hwy, alpha = class))
Warning: Using alpha for a discrete variable is not advised.
Abbildung 13.5: Das Argument alpha= ist der Füllgrad der Punkte. Die Färbung hier findet wieder bezüglich eines kategorialen Merkmals statt, was aber schlecht ist, da alpha= Werte zwischen 0 und 1 annimmt und nicht für die Nutzung kategorialer Merkmale geeignet ist. 
mpg |> ggplot() + 
       geom_jitter(aes(x = displ, y = hwy, alpha = cty))
Abbildung 13.6: Für metrische Merkmale oder um Überlappungen zu zeigen ist das Argument alpha= geeignet.

Die Funktion aes() steht für aesthetic. In ihren Argumenten werden den visuellen Eigenschaften der Grafik Merkmale der Beobachtungen zugeordnet, wie z.B. ordnet man der Farbe (color=) oder der Sättigung (alpha=) die Klasse zu.

Bei welche geometrischen Funktionen welche aes()-Argumente existieren, bzw. welche zwingend benötigt werden, hängt von der Grafik ab, die erzeugt werden soll. Die geometrische Funktion geom_point() zum Beispiel benötigt zwingend die Argumente x= und y= in der Funktion aes(),

13.2.1 Warnungen

mpg |> ggplot() +
       geom_point(aes(x = displ, y = hwy, 
                      alpha = class))
Warning: Using alpha for a discrete variable is not advised.
Abbildung 13.7: Warnungen 1: das Argument alpha= ist nicht für kategoriale Daten geeignet! 
mpg |> ggplot() + 
       geom_point(mapping = aes(x = displ, y = hwy, shape = class))
Warning: The shape palette can deal with a maximum of 6 discrete values because more
than 6 becomes difficult to discriminate
ℹ you have requested 7 values. Consider specifying shapes manually if you need
  that many of them.
Warning: Removed 62 rows containing missing values or values outside the scale range
(`geom_point()`).
Abbildung 13.8: Warnungen 2: das Argument shape= ist nur geeignet, wenn das Merkmal nicht zu viele Ausprägungen hat. Im Beispiel können nur 6 der 7 Ausprägungen dargestellt werden.

Manche Aesthetics sind zwingend notwendig, andere Aesthetics (hier: shape= und alpha=) liefern ggf. Warnungen allerdings werden die Grafiken trotzdem dargestellt, wenn auch nicht immer komplett, wie im Beispiel shape zu sehen ist!

  • Es ist möglich, auch außerhalb der Funktion aes() Argumente, die das gesamte Aussehen der Grafik beeinflussen, anzuführen.
mpg |> ggplot() + 
       geom_point(aes(x = displ, y = hwy), 
                  col = "blue",
                  alpha = 0.2,
                  position = "jitter")
Abbildung 13.9: Das Argument color= kann bei den meisten geometrischen Funktionen auch außerhalb der Funktion aes() stehen, allerdings nur, wenn eine Farbe zugewiesen ist und kein Merkmal.

werden alle Punkte blau gezeichnet (col = "blue") und haben einen Färbung / Sättigung von 20\% (alpha = 0.2).

  • Diese von den Daten unabhängige Veränderung erzeugt keine Legende.
  • Die dunklere Färbung mancher Punkte kommt aufgrund der Überlagerung mehrerer Punkte zustande.
  • In Abbildung 13.9 wurde zusätzlich die Option position = "jitter" gesetzt, um die Punkte leicht zufällig gegeneinander zu verschieben.
Aufgabe
  1. Wieso sind in der folgenden Grafik die Punkte rot und nicht blau?
mpg |> ggplot() + 
       geom_point(mapping = aes(x = displ, y = hwy, color = "blue"))

  1. Wie lautet der korrekte Code um die Punkte blau einzufärben?

  2. Bilden Sie eine numerische Variable auf die Argumente color=, size= und shape= ab. Was fällt auf und was ist der Unterschied zu einer kategoriellen Variablen wie z.B. class?

  3. Was passiert, wenn mehrere Variablen auf die gleichen Argumente abgebildet werden?

  4. Was macht das stroke=-Argument? Verwedenen Sie ggf. die Hilfe für geom_point().

13.3 Facetten

Die Funktionen facet_wrap() und facet_grid() bilden (neben den Aesthetics) eine Möglichkeit, ein zusätzliches kategoriales Merkmal sichtbar zu machen.

mpg |> ggplot() + 
       geom_point(aes(x = displ, y = hwy)) + 
       facet_wrap(~ class, nrow = 2)
Abbildung 13.10: Facetten bieten eine weitere Möglichkeit ein kardinales Merkmal sichtbar zu machen.

Die Funktion facet_wrap() benötigt ein Argument (nach einer Tilde) und spaltet die Grafik nach diese Variable auf. Es entstehen soviele Untergrafiken wie das Merkmal Ausprägungen hat. Das Argument nrow= gibt an, auf wie viele Zeilen diese Grafiken aufgeteilt werden sollen. Alternativ kann auch das Argument ncol= verwendet werden, wobei damit die Anzahl der Spalten angegeben werden kann.

mpg |> ggplot() + 
       geom_point(aes(x = displ, y = hwy)) + 
       facet_grid(drv ~ class)
Abbildung 13.11: Die Funktion facet_grid() bietet eine Möglichkeit sogar zwei kardinale Merkmale sichtbar zu machen.

Die Funktion facet_grid() benötigt zwei Argumente. Die Ausprägungen des ersten Arguments (im Beispiel drv) stehen in den Zeilen, die Ausprägungen des zweiten Arguments in den Spalten.

Es ist auch möglich die Funktion facet_grid() wie facet_wrap() zu nutzen, wenn das erste Argument vor der Tilde eine . ist. Man nennt eine Zuordnung y~x in R eine Formel und Abbildung 13.11 wird zu:

mpg |> ggplot() + 
       geom_point(mapping = aes(x = displ, y = hwy)) + 
       facet_grid(. ~ cyl)

13.4 Geometrische Objekte

Wir haben schon in Kapitel 3 gesehen, dass man mehrere geometrische Funktionen in einer Grafik zusammenbringen kann. wie zum Beispiel in der folgenden Grafik.

mpg |> ggplot() + 
       geom_point(aes(x = displ, y = hwy)) +
       geom_smooth(aes(x = displ, y = hwy))
Abbildung 13.12: Zwei geometrische Funktionen in einer Grafik

Die Reihenfolge ist wichtig, da die verschiedenen Schichten von vorne aufgebaut werden. so kann man in Abbildung 13.12 sehen, dass die blaue Kurve nach den Punkten gezeichnet wurde.

  • Welche geometrische Objekte verwendet werden können bzw. sollen, hängt von den Daten ab. Dabei spielt sowohl die Anzahl der darzustellenden Merkmale als auch die Art der Merkmale (kategorial oder metrisch) eine Rolle.

  • Um Redundanzen im Code zu vermeiden, können globale Aesthetics in die ggplot-Funktion geschrieben werden.

Abbildung 13.12 kann auch geschrieben werden als

mpg |> ggplot(aes(x = displ, y = hwy)) +
       geom_point() +
       geom_smooth()

Aesthetics, die nur eine geometrische Funktion betreffen, werden hingegen lokal in die betreffenden geometrische Funktion geschrieben.

mpg |> ggplot(aes(x = displ, y = hwy)) +
       geom_point(aes(color = class)) + 
       geom_smooth(color = "black")
Abbildung 13.13: Die Daten für die Punkte und die Kurve sind die gleichen, daher können diese in die Funktion ggplot() geschrieben werden. Die Farbe der Punkte bzw. der Kurve betrifft allerdings nur die jeweiligen geometrischen Funktion. Es ist bemerken, dass die Farbe der Punkte am Merkmal class hängt weswegen die color = class innerhalb der Funktion aes() stehen muss. Bei color = "black" ist dies nicht der Fall.

Bemerkungen zu Abbildung 13.13:

  • In der Funktion ggplot() stehen die Mermale displ und hwy. Diese betreffen alle folgenden geometrischen Funktionen. Da es sich um Merkmale handelt muss die Zuweisung innerhalb der Funktion aes() erfolgen.

  • Das Merkmal class in der geometrishen Funktion geom_point() legt nur die Farbgebung der Punkte fest, da es sich bei class auch um ein Merkmal handelt muss die Zuweisung color = class innerhalb der Funktion aes() erfolgen und es werden keine Anführungszeichen gesetzt.

  • In der zweiten geometrischen Funktion wird festgelegt, dass die Linie der Kurve schwarz sein soll color = "black". Dies betrifft ausschließlich die Kurve, und da es sich nicht um ein Merkmal handelt, steht dies direkt als Argument in der Funktion geom_smooth().

Weitere Beispiele

mpg |> ggplot() + 
       geom_smooth(aes(x = displ, y = hwy, linetype = drv))
Abbildung 13.14: Zwei metrische und ein kategoriales Merkmal. Die Kurven werden nur auf dem Bereich dargestellt in dem Daten vorhanden sind. 
mpg |> ggplot(mapping = aes(x = displ, y = hwy, color = drv)) + 
       geom_point() + 
       geom_smooth(se = FALSE)
Abbildung 13.15: Die drei Merkmale sind global definiert, so dass sie für beide geometrischen Funktionen gültig sind.

Bemerkungen:

  • Das Argument se = FALSE im unteren Beispiel schaltet die Konfidenzintervalle (grauer Bereich um die Kurve) aus.
  • Welche Argumente die jeweiligen geometrischen Funktionen haben, kann man mit der Hilfe-Funktion erfahren, z.B.
?geom_smooth    # oder  help(geom_smooth)

13.4.1 Geometrische Objekte für gefilterte Daten

Es ist möglich, für verschiedene Schichten auch verschiedene Daten zu nutzen.

  • Die Funktion filter() filtert Datenzeilen nach einem vorgegebenen Kriterium.
  • In den Beispielen werden die globalen Daten durch die lokalen überschrieben – allerdings nur für die jeweilige Schicht!
mpg |> ggplot(aes(x = displ, y = hwy)) + 
       geom_point(mapping = aes(color = class)) + 
       geom_smooth(data = filter(mpg, class == "subcompact"), 
                   se = FALSE) + 
       theme(legend.position = "bottom")   # Legende unten
Abbildung 13.16: Die drei Merkmale sind global definiert, so dass sie für beide geometrischen Funktionen gültig sind. 
mpg |> ggplot(aes(x = displ, y = hwy)) + 
       geom_point() + 
       geom_point(data = filter(mpg, class == "2seater"), 
                  col = "red") + 
       geom_smooth(data = filter(mpg, class != "2seater"))
Abbildung 13.17: In zwei der Funktionen werden gefilterte Daten verwendet. Diese müssen der geometrischen Funktion über das Argument data= übergeben werden.

Die Reihenfolge ist wichtig, da im letzten Beispiel ein Teil der Punkte aus der Funktion geom_point() durch die zweite geom_point() Funktion ,,verdeckt’’ werden.

13.5 Statistische Transformationen

In diesem Kapitel werden wir die Datentabelle diamonds aus dem ggplot2 Paket verwenden.

diamonds
# A tibble: 53,940 × 10
   carat cut       color clarity depth table price     x     y     z
   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
 1  0.23 Ideal     E     SI2      61.5    55   326  3.95  3.98  2.43
 2  0.21 Premium   E     SI1      59.8    61   326  3.89  3.84  2.31
 3  0.23 Good      E     VS1      56.9    65   327  4.05  4.07  2.31
 4  0.29 Premium   I     VS2      62.4    58   334  4.2   4.23  2.63
 5  0.31 Good      J     SI2      63.3    58   335  4.34  4.35  2.75
 6  0.24 Very Good J     VVS2     62.8    57   336  3.94  3.96  2.48
 7  0.24 Very Good I     VVS1     62.3    57   336  3.95  3.98  2.47
 8  0.26 Very Good H     SI1      61.9    55   337  4.07  4.11  2.53
 9  0.22 Fair      E     VS2      65.1    61   337  3.87  3.78  2.49
10  0.23 Very Good H     VS1      59.4    61   338  4     4.05  2.39
# ℹ 53,930 more rows
glimpse(diamonds)
Rows: 53,940
Columns: 10
$ carat   <dbl> 0.23, 0.21, 0.23, 0.29, 0.31, 0.24, 0.24, 0.26, 0.22, 0.23, 0.…
$ cut     <ord> Ideal, Premium, Good, Premium, Good, Very Good, Very Good, Ver…
$ color   <ord> E, E, E, I, J, J, I, H, E, H, J, J, F, J, E, E, I, J, J, J, I,…
$ clarity <ord> SI2, SI1, VS1, VS2, SI2, VVS2, VVS1, SI1, VS2, VS1, SI1, VS1, …
$ depth   <dbl> 61.5, 59.8, 56.9, 62.4, 63.3, 62.8, 62.3, 61.9, 65.1, 59.4, 64…
$ table   <dbl> 55, 61, 65, 58, 58, 57, 57, 55, 61, 61, 55, 56, 61, 54, 62, 58…
$ price   <int> 326, 326, 327, 334, 335, 336, 336, 337, 337, 338, 339, 340, 34…
$ x       <dbl> 3.95, 3.89, 4.05, 4.20, 4.34, 3.94, 3.95, 4.07, 3.87, 4.00, 4.…
$ y       <dbl> 3.98, 3.84, 4.07, 4.23, 4.35, 3.96, 3.98, 4.11, 3.78, 4.05, 4.…
$ z       <dbl> 2.43, 2.31, 2.31, 2.63, 2.75, 2.48, 2.47, 2.53, 2.49, 2.39, 2.…

Die Datentabelle diamonds enthält 10 Merkmale in den Spalten und 53,940 Beobachtungen (Ausprägungen) in den Zeilen. Die Merkmale cut, color und clarity sind kategorial, genauer ordinal (<ord>), das heißt sie können angeordnet werden. Alle anderen Merkmale sind metrisch (<dbl>).

Tabelle 13.2: Zusammenfassung Merkmale der Datentabelle diamonds.
Merkmal Bedeutung Skalentyp in R
carat Gewicht der Diamanten metrisch <dbl>
cut Qualität des Schnitts ordinal <ord>
color Diamantenfarbe D (beste) bis J (schlechteste) ordinal <ord>
clarity Klarheit der Diamanten ordinal <ord>
depth Absolute Tiefe in Prozent metrisch <dbl>
table Breite Oberseite relativ zu breitestem Punkt metrisch <dbl>
price Preis in US Dollar metrisch <int>
x Länge in mm metrisch <dbl>
y Breite in mm metrisch <dbl>
z Tiefe in mm metrisch <dbl>
Aufgabe: Eigenschaften diamonds

  1. Das Merkmal clarity, die Klarheit der Diamanten, ist ordinal. Welche Ausprägungen gibt es und wie lautet die Ordnung?

  2. Die Funktion summary() hilft einen Überblick über eine Datentabelle zu bekommen.

  • Was zeigt die Funktion an?
  • Gibt es Werte in der Datentabelle diamonds, die Ihnen seltsam vorkommen?

13.5.1 Säulendiagramme

diamonds |> ggplot() + 
            geom_bar(mapping = aes(x = cut))
Abbildung 13.18: Ein einfaches Säulendiagramm des Merkmals cut.

Auf der x-Achse der Grafik ist die Variable cut abgetragen. Auf der y-Achse ist die Anzahl count des jeweiligen Schliffs abgetragen, allerdings ist count keine Variable des Datensatzes diamonds, sondern eine berechnete Größe: sie entspricht der Anzahl, wie oft die jeweilige Ausprägung in der Variablen cut vorkommt. Wir bezeichnen das Berechnen von solchen Größen, die zum Erstellen von Grafiken notwendig sind als statistische Transformationen.

Man kann erkennen, dass bessere Diamanten häufiger verkauft wurden.

diamonds |> count(cut)
# A tibble: 5 × 2
  cut           n
  <ord>     <int>
1 Fair       1610
2 Good       4906
3 Very Good 12082
4 Premium   13791
5 Ideal     21551

Beispiele zu statistischen Transformationen:

Einige Funktionen, wie zum Beispiel das Streudiagramme (scatter plot) – erzeugt mit geom_point() stellen die Rohdaten dar. Andere Funktionen berechnen neue Werte, um die Daten darzustellen.

  • Säulendiagramme (geom_bar(), geom_dotplot(), Histogramme (geom_histogram()) und Häufigkeitspolygone (geom_freqpoly()) stellen Anzahlen grafisch dar, die aus den Daten berechnet wurden.

  • Geglätteten Kurven (geom_smooth()) liegt ein Modell zugrunde. Die gezeichnete Linie / Bereiche sind Vorhersagen durch ebendieses Modell.

  • Boxplots (geom_boxplot()) berechnen robuste Lage- und Streumaße einer Verteilung und stellen diese dar.

diamonds |> ggplot() + 
            geom_bar(aes(x = cut))
Abbildung 13.19: Säulendiagramm 
diamonds |> ggplot() + 
            geom_smooth(aes(x = carat, y = price))
`geom_smooth()` using method = 'gam' and formula = 'y ~ s(x, bs = "cs")'
Abbildung 13.20: Geglättete Kurve 
diamonds |> ggplot() + 
            geom_boxplot(aes(x = color, y = price))
Abbildung 13.21: Boxplot
Abbildung 13.22: Die Grafik zeigt, wie aus einer Datentabelle die zugehörigen Anzahlen zugewiesen werden um daraus das Säulendiagramm zu erstellen. (Quelle: r4ds)
  • Die Funktion geom_bar() startet mit der Datentabelle diamonds
  • Danach transformiert geom_bar() die Datentabelle derart, dass eine Datentabelle mit den Ausprägungen von cut sowie den zugehörigen Anzahlen count entsteht.
  • Zuletzt werden die transformierten Daten herangezogen, um die Grafik zu erstellen, wobei die Ausprägungen von cut auf der x-Achse und count auf der y-Achse abgebildet werden.

Säulendiagramm ohne Berechnung der Anzahlen

  • Statt die Anzahl der Einträge einer Ausprägung zu zählen, gibt es die Möglichkeit, die Ausprägung selbst als Wert zu nehmen.
  • Im folgenden Beispiel wird eine solche Tabelle erzeugt.
daten <- tribble(~schnitt,      ~haeufigkeit,  
                  "Fair",        1610,
                  "Good",        4906,
                  "Very Good",  12082,
                  "Premium",    13791,
                  "Ideal",      21551
                 )
daten |> ggplot() +
         geom_bar(aes(x = schnitt, y = haeufigkeit), 
                  stat = "identity")
Abbildung 13.23: Die Ausprägung des Merkmals haeufigkeit wird als Wert verwendet. Es findet keine statistische Transformation im Sinne der Abbildung 13.22 statt.

Wollen wir nun aus dieser Datentabelle ein Säulen- oder Balkendiagramm erstellen, so erfordert dies keine statistische Transformtion in dem Sinn, dass die Anzahlen gezählt werden müssen bevor sie dargestellt werden. Statt dessen soll der im Merkmal haeufigkeit angeführte Wert verwendet werden.

  • Dies geschieht mit dem Argument stat = "identity".

13.5.2 Anteile und andere statistische Kenngrößen

Oft ist es auch interesssant relative statt absolute Größen darzustellen.

diamonds |> ggplot() +
            geom_bar(aes(x = cut, 
                     y = after_stat(prop),
                     group = 1))
Abbildung 13.24: Mit dem Argument stat="identity" werden die Ausprägungen im Merkmal haeufigkeit zur Darstellung verwendet. Die Anordnung auf der x-Achse ist hier alphabetisch, da das Merkmal schnitt kein Faktor ist (diesen könnte wir auch erstellen, soll aber der Übersicht halber hier nicht passieren).

Barplot fill= und colour=

  • Man kann Säulendiagramme mit Hilfe der Argumente fill= bzw. colour= (oder auch color=) einfärben.
  • Das Argument colour= bzw. color= bezieht sich dabei auf den Rand der Säulen.
  • Das Argument fill= bezieht sich auf die Füllfarbe der Säulen.
  • Möchte man keine flächige Färbung haben, so kann dies mit fill=NA (not available) geschehen. Ansonsten wird die Farbe des aktuellen Farbschemas verwendet.
  • Mit den Argumenten innerhalb von aes() wird der Füllung bzw. Umrandung ein Merkmal zugeordnet (hier cut) und eine Legende hinzugefügt.
diamonds |> ggplot() + 
            geom_bar(aes(x = cut, 
                         colour = cut),
                     fill = NA)
Abbildung 13.25: Bei der Funktion geom_bar() bezieht sich das Argument colour= auf den Rand der Balken. Die Füllung geschieht mit fill=. 
diamonds |> ggplot() + 
            geom_bar(aes(x = cut, fill = cut))
Abbildung 13.26: Jedes Dieser Argumente kann auch bezüglich eines Merkmals gefärbt werden. Auch wenn dies aufgrund der Redundanz im Allgemeinen nicht zu empfehlen ist.
Abbildung 13.27: Die Grafik zeigt, wie aus einer Datentabelle die zugehörigen Farben generiert und zugewiesen werden. (Quelle: r4ds)
  • Gestartet wird mit dem Datensatz diamonds.
  • Danach berechnet stat_count() die Anzahl der Beobachtungen für jede Ausprägung von cut.
  • Die Häufigkeit jeder Ausprägung wird mit einer Säule dargestellt.
  • Für jede Ausprägung von cut erhält fill= einen anderen Wert, also eine andere Farbe.
  • Schließlich wird ein kartesisches Koordinatensystem generiert und
  • die y-Variable auf die berechnete Anzahl sowie die x-Variable auf die Ausprägungen von cut abgebildet.

13.5.3 Platzierung der Balken / Säulen

  • Nutzt man das Argument fill= für ein weiteres Merkmal, so erhält man ein gestapeltes Säulendiagramm.

  • Möchte man dies nicht haben, so kann man das Argument position= nutzen. Es kann die Werte identity, dodge und fill annehmen. Dabei bedeutet der Wert fill, dass alle Säulen gleich hoch gezeichnet werden, um Verhältnisse gut erkennen zu können.

diamonds |> ggplot() +  
            geom_bar(aes(x = cut, fill = clarity))
Abbildung 13.28: Gestapelts Säulendiagramm: Geschieht das Füllen der Säulen (oder Balken) in der Funktion geom_bar() in abhängigkeit von einem Merkmal, so sind die entstehenden Teilsäulen gestapelt. 
diamonds |> ggplot() + 
            geom_bar(aes(x = cut, fill = clarity), 
            position = "dodge")
Abbildung 13.29: Durch das Argument position = "dodge" können die Teilsäulen auch nebeneinander dargestellt werden. So ist es möglich zwei kardinale Merkmale gleichzeitig darzustellen und man erhält gruppierte Säulendiagramme.

13.6 Koordinatenfunktion

13.6.1 Erstellen von Balkendiagrammen

Es gibt zwei Möglichkeiten, Balkendiagramme zu erstellen:

  • Man benutzt die y-Koordinate in der Funktion aes().
  • Man benutzt die x-Koordinate in der Funktion aes() und tauscht danach mit der Funktion coord_flip() die x- mit der y- Koordinate.
diamonds |> ggplot() + 
            geom_bar(aes(y = cut, fill = cut))
Abbildung 13.30: Das Ertsellen eines Balkendiagramms.

Das gleiche Ergebnis erhält man mittels

diamonds |> ggplot() + 
            geom_bar(aes(x = cut, fill = cut)) +  
            coord_flip()

Der Vorteis des Balkendiagramms wird insbesondere dann sichtbar, wenn wir sehr viele (nominale) Merkmale gleichzeitig darstellen wollen. Während die Beschriftung eines Säulendiagramms dann schwieg (zu lesen) wird, ist dies bei Balkendiagrammen kein Problem.

13.6.2 Horizontale Boxplots

Die Funktion coord_flip() kann auch bei anderen geometrischen Objekten genutzt werden. Insbesondere bei kategorialen Variablen (hier class) sind die Namen der Ausprägungen oft lang, so dass es sinnvoll ist, diese horizontal untereinander zu schreiben (unteres Beispiel).

mpg |> ggplot(aes(x = class, y = hwy)) + 
       geom_boxplot()
Abbildung 13.31: Auch andere Funktionen, bei denen nominale Merkmale dargestellt werden, können durch coord_flip() gespiegelt werden. 
mpg |> ggplot(aes(x = class, y = hwy)) + 
       geom_boxplot() +
       coord_flip()
Abbildung 13.32: Wieder ist ein Vorteil, dass die Ausprägungen der Merkmale sehr gut geesen werden können und auch eine große Anzahl kein Problem bei der Darstellung ist.

13.7 Themes

13.7.1 Die Funktionen themes_*()

Um das Erscheinungsbild der Grafik (Achsen, Hintergrund, Schriftart, Schriftgröße) zu beeinflussen gibt es verschiedene ,,Themes’’. Ich habe ein paar interessante aus dem Basispaket hier einmal dargestellt.

Die Argumente der Funktionen sowie eine ausführliche Liste findet man auf der Seite ggplot2 - Complete themes.

Darüber hinaus gibt es noch weitere Pakete, die Themes zur Verfügung stellen, zum Beispiel das Paket ggthemes. Das Paket liefert auch noch geometrische Funktionen und Scales.

13.7.2 Achsenbeschriftung

Mit der Funktion theme() kannn alles rund um die Achsenbeschriftung geändert werden. Die allgemeine Syntax lautet + theme(ELEMENT.NAME = ELEMENT_FUNKTION()), wobei ELEMENT.NAME und element_FUNKTION wieder Platzhalter sind. Mit ELEMENT.NAME wird angegeben was geändert werden soll und element_FUNKTION() gibt an wie etwas geändert wir.

Für weitere Informationen zu Themes und wie man einzelne Elemente ändert, verweise ich auf ggplot2: Elegant Graphics for Data Analysis, die ultimative Anleitung für ggplot2.