20 Funktionen
Das Kapitel ist noch nicht fertig und ändert sich in den nächsten Tag noch!
20.1 Grundlagen
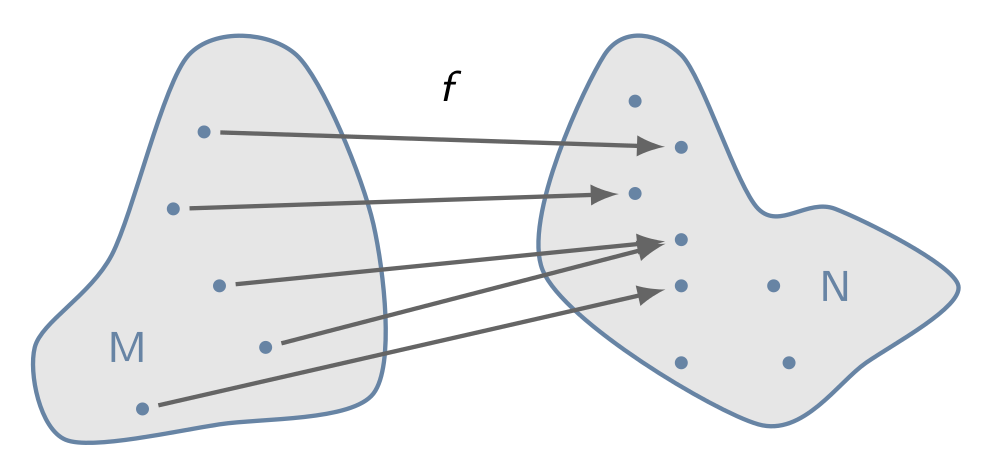
Bemerkung
Bei der Schreibweise für das Urbild muss man ein wenig aufpassen, da Hoch minus Eins mehrfach belegt ist. Es wird auch für die Umkehrfunktion verwendet und die Potenzschreibweise für einen Kehrwert sieht ähnlich aus.
Beispiel
Gegeben die Funktion g: \mathbb{R} \to \mathbb{R} mit y = g(x) = x^2.
- Das Bild der Funktion sind nun alle alle Werte, die wirklich angenommen werden. In diesem Beispiel werden nur nicht-negative Werte angenommen und es gilt
\begin{align*} \textsf{Bild}(g) = \mathbb{R}_{\ge 0} = [0,\infty). \end{align*}
- Das Urbild gibt man immer bezüglich eines Wertes an. So ist zum Beispiel das Urbild von y = 4 die Menge g^{-1}(4) = \{-2, 2\}, da sowohl -2 als auch 2 von g auf die 4 abgebildet werden.
Bemerkungen
Die Injektivität bedeutet damit, dass für jeden Wert y aus der Wertemenge W \subseteq N genau ein Wert x aus der Definitionsmenge M existiert, so dass f(x) = y ist. Diese Eigentschaft ist nochwendig, wenn man eine eindeutige Umkehrung benötigt, wenn man also einem y-Wert einen eindeutigen x-Wert zuordnen muss.
Die Surjektivität bedeutet, dass jeder Wert der Zielmenge angenommen wird. Anders ausgedrückt, dass Bildmenge und Zielmenge identisch sind. Surjektivität kann man offenbar immer erreichen, wenn man die Zielmenge auf die Wertemenge der Funktion einschränkt.
Bijektivität entspricht einer 1:1 Zuordnung von Definitions- und Zielmenge über die Funktion f.
Beispiele
Die Funktion f: \mathbb{R}_{+} \to \mathbb{R} mit f(x) = x^2 ist injektiv, aber nicht surjektiv, da nicht alle Werte aus \mathbb{R} angenommen werden.
Die Funktion f: \mathbb{R} \to \mathbb{R}_{\ge 0} mit f(x) = x^2 ist surjektiv, aber nicht injektiv, da zwar alle Werte aus der Zielmenge angenommen werden, aber f(-x) = f(x) ist, zum Beispiel f(-2) = f(2) = 4.
Die Funktion f: \mathbb{R} \to \mathbb{R} mit f(x) = 2x ist bijektiv, da es für jeden y-Wert genau einen x-Wert gibt und jeder Wert der Zielmenge angenommen wird.
Wir wollen uns nun auf reellwertige Funktionen beschränken, das sind Funktionen deren Zielmenge die reellen Zahlen \mathbb{R} sind.
Zur Visualisierung von reellen Funtionen nutzen wir Graphen.
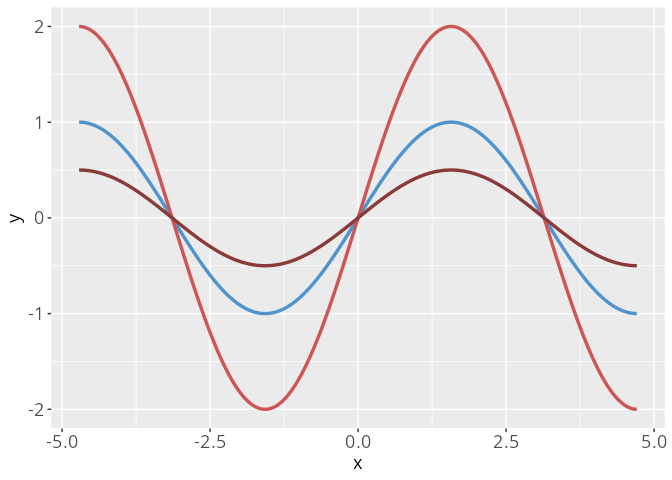
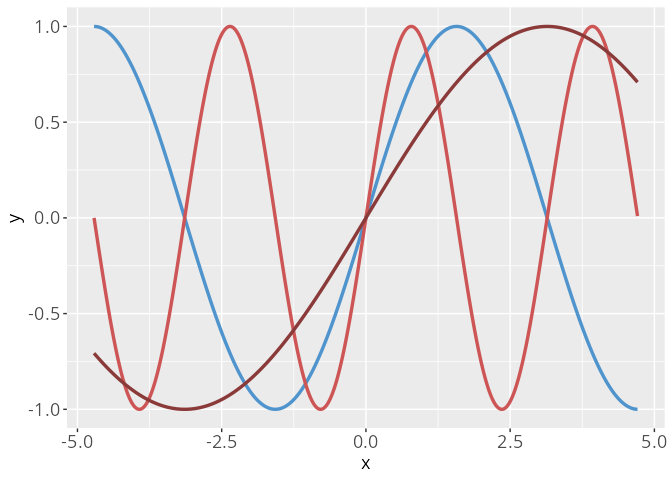
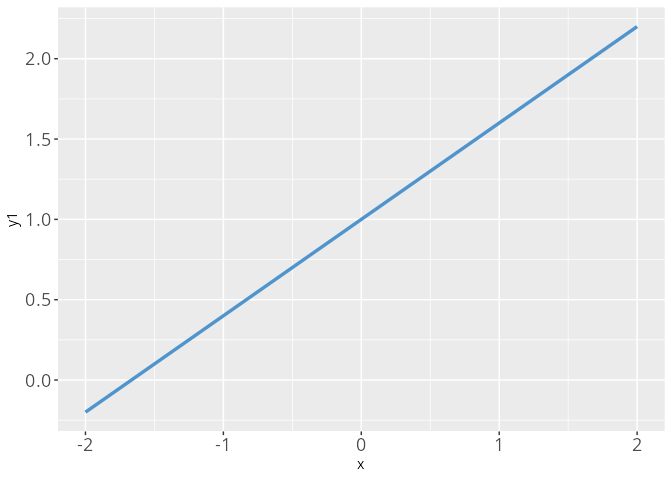
Beispiele: die Top 10 Graphen

20.2 Lineare Funktionen
Eine wichtige Klasse der Funktionen sind die affin-linearen Funktionen.
20.2.1 Darstellungen linearer Funktionen
Normalform
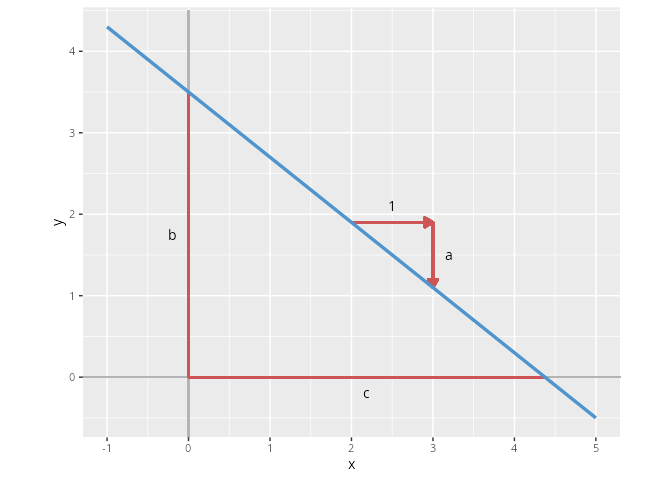
Jede nicht zur y-Achse parallele Gerade kann in der Normalform y = f(x) = ax + b dargestellt werden. Die Parametern a und b können aus dem Graphen abgelesen werden, da sie eine geometrische Bedeutung haben.
- Der Parameter a \in \mathbb{R} ist die Steigung und
- b \in \mathbb{R} ist der Achsenabschnitt
der Funktion. Ist der Parameter a>0, so ist die Funktion streng monoton steigend geht und der Graph verläuft von unten links nach oben rechts, ist a=0 so ist der Graph eine Parallele zur x-Achse und im Fall von a<0 ist die Funktion streng monoton fallend und der Graph verläuft von oben links nach unten rechts.
Zweipunktsteigung
Gibt man zwei verschiedene Punkte P_1 = (x_1, y_1) und P_2 = (x_2, y_2) vor, wobei y_1 \neq y_2 gelten soll, dann gilt:
\begin{align*} \frac{\Delta y}{\Delta x} = \frac{f(x_2) -f(x_1)}{x_2 - x_1} = \frac{ax_2 + b - (ax_1 + b)}{x_{2} -x_1} = a. \end{align*}
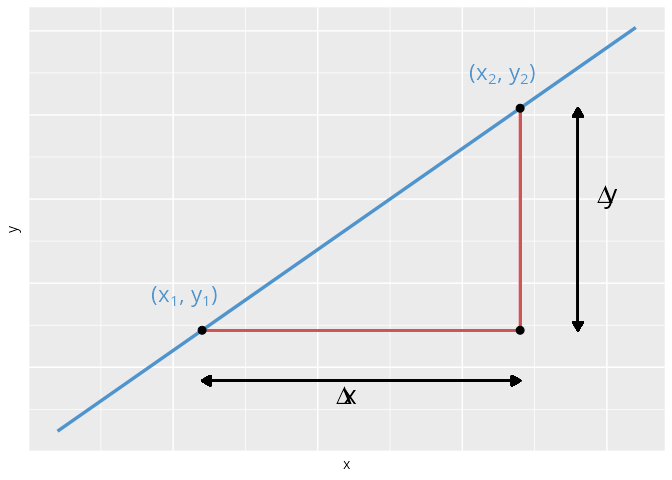
Damit ist die Steigung einer Geraden, die durch zwei beliebige, verschiedenen Punkte P_1 = (x_1, y_1) und P_2 = (x_2, y_2) geht, konstant. Die Gerade können wir kann dann mit Hilfe der Gleichung
\begin{align*} \frac{y_2 - y_1}{x_2 - x_1} = \frac{y_1 - y}{x_1 - x} \end{align*}
beschreiben. Lösen wir diese Gleichung nach y auf, so erhalten wir
\begin{align*} y = \underbrace{\frac{y_2 - y_1}{x_2 - x_1}}_{a} x + \underbrace{y_1 - \frac{y_2 - y_1}{x_2 - x_1} x_1}_{b} \end{align*}
Damit ist der Term \frac{y_2 - y_1}{x_2 - x_1} = a die Steigung und y_1 - \frac{y_2 - y_1}{x_2- x_1}x_1 = b der Achsenabschnitt.
Punktsteigungsform
Ist ein Punkt P_1 = (x_1, y_1) sowie die Steigung a gegeben, so nutzen wir die Punktsteigungsform. Aus der Formel
\begin{align*} \frac{\Delta y}{\Delta x} = \frac{y - y_1}{x - x_1} = a. \end{align*}
erhält man
\begin{align*} y - y_1 = a (x-x_1) \quad \text{bzw.} \quad y = a (x-x_1) + y_1 \end{align*}
Ausmultiplieren liefert, dass y_1 - ax_1 = b der Achsenabschnitt ist.
Achsenabschnittsform
Haben wir die Nullstelle c, sowie den Achsenabschnitt b gegeben, also die Schnittpunkte mit den Koordinatenachsen (c, 0) und (0, b), so können wir die Geradengleichung in der Form
\begin{align*} \frac{x}{c} + \frac{y}{b} = 1. \end{align*}
schreiben. Man nennt dies die Achsenabschnittsform. Offenbar funktioniert dies nicht mit allen Geraden, denn weder c noch b dürfen in der obigen Gleichung 0 sein, und auch zur x-Achse parallele Geraden können nicht auf diese Weise beschrieben werden. Durch einfaches Umformen erhalten wir den Zusammenhang zwischen den Achsenabschnitten und der Steigung a = -\frac{b}{c}.
Beispiel
Eine Gerade habe die Steigung m = -3 und gehe durch den Punkt P = (4, -7). Wie lautet die Normalenform und die Achsenabschnittsform?
Antwort: Es gilt \begin{align*} \frac{y - (-7)}{x -4} = -3 \qquad \implies \qquad y = -3x+5. \end{align*}
Für die Achsenabschnittsform ergibt sich daraus
\begin{align*} \frac{x}{\frac{5}{3}} + \frac{y}{5} = 1 \end{align*}
20.2.2 Allgemeine Geradengleichung
- Jeder Funktionsterm der Form y = f(x) = ax+b kann in ein allgemeine Geradengleichung gebracht werden.
- In die andere Richtung ist das nicht richtig. Nur für den Fall \beta \neq 0 kann G in einen Funktionsterm der Form y = f(x) gebracht werden. In diesem Fall ist dann \begin{align*} f(x) = y = -\frac{\alpha}{\beta}x - \frac{\gamma}{\beta}. \end{align*}
- Für den Fall \beta = 0 und \alpha \neq 0 erhält man \alpha x + \gamma = 0, also x = -\frac{\gamma}{\alpha}. Das heißt x ist eine Konstante und y kann jeden beliebigen Wert annehmen. Geraden mit den Koordinaten der Form (-\frac{\gamma}{\alpha}, y) sind Parallelen zur y-Achse und keine Funktionen.
20.3 Quadratische Funktionen
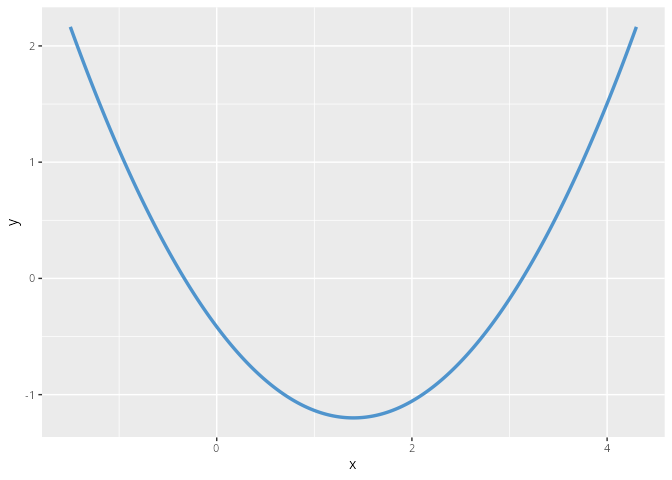
Mit Hilfe der quadratischen Ergänzung kann man eine quadratische Funktion in ihre Scheitelpunktform
\begin{align*} f(x) = a(x-x_s)^2 + y_s \qquad \text{mit} \quad x_s = -\frac{b}{2a} \quad \text{und} \quad y_s = c-\frac{b^2}{4a} \end{align*}
bringen. Der Punkt S = (x_s, y_s) ist der Scheitel der Funktion. Im Fall a < 0 ist die Stelle x_s das globale Maximum, im Fall von a > 0 das globale Minimum.
20.4 Exponentialfunktion
Wir wollen die Exponentialfuntion \exp definieren. Da diese keine algebraische Funktion ist, gestaltet sich die Definition ein wenig komplizierter.
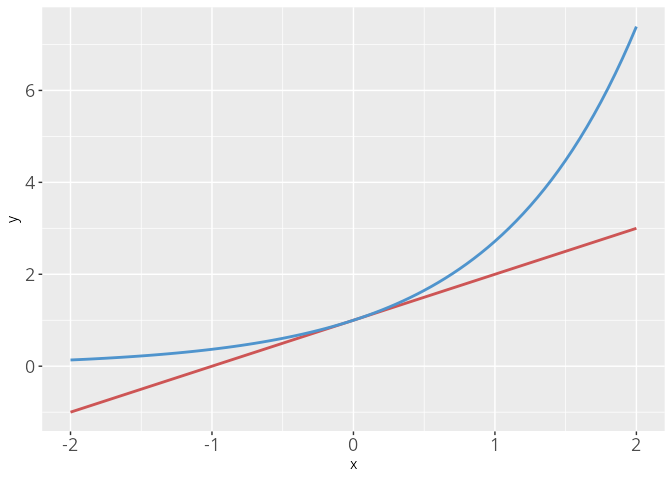
Bemerkung
Man nennt die Gleichung \exp(x+y) = \exp(x) \cdot \exp(y) die Funktionalgleichung der Exponentialfunktion.
Nach der eher formalen Definition, stellt sich heraus, dass die Exponentialfunktion mit Hilfe der Eulerzahl \textsf{e}=2,718281828459045... geschrieben werden kann:
\begin{align*} \exp(x) = \textsf{e}^x \end{align*}
20.5 Logarithmusfunktion
Die Funktion \exp: \mathbb{R} \to \mathbb{R} ist injektiv und damit auf dem gesamten Definitionsbereich eindeutig umkehrbar. Diese Umkehrung wird der natürliche Logarithmus sein. Gilt y = \exp(x), so stellt sich die Frage: ,,Für welches x nimmt die Funktion \exp(x) den vorgegebenen Wert y an?’’
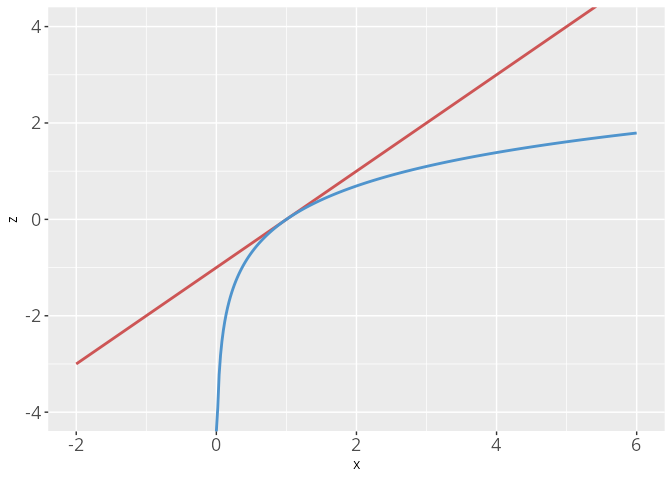
Da die Funktion \ln: \mathbb{R}_{>0} \to \mathbb{R} die Umkehrfunktion der Exponentialfunktion \exp: \mathbb{R} \to \mathbb{R} ist, gilt für alle x \in \mathbb{R} und y \in \mathbb{R}_{>0}
\begin{align*} \exp(\ln(y)) = y \qquad \textsf{und} \qquad \ln(\exp(x)) = x. \end{align*}
20.5.1 Basiswechsel Exponentialfunktion und Logarithmen
Wir wollen ab nun die Exponentialschreibweise verwenden. Da \textsf{e}^{\ln(a)} = a gilt, kann man auch jede andere positive reelle Zahl a \in \mathbb{R}_{>0} als Basis definieren, denn es gilt
\begin{align*} a^x = (\textsf{e}^{\ln(a)})^x = \textsf{e}^{\ln(a)x} \end{align*}
20.6 Transformationen
Gegeben sei eine Funktion f: \mathbb{R} \to \mathbb{R} mit x \mapsto f(x). Ziel ist es nun eine zweite Funktion g: \mathbb{R} \to \mathbb{R} zu definieren, die sich durch eine Transformation aus der ersten ergibt. Dies kann eine Translation, das heißt eine Verschiebung in x- oder y-Richtung sein, eine Stauchung oder Streckung in x- oder y-Richtung oder eine Spiegelung an der x- oder y-Achse.
20.6.1 Translationen
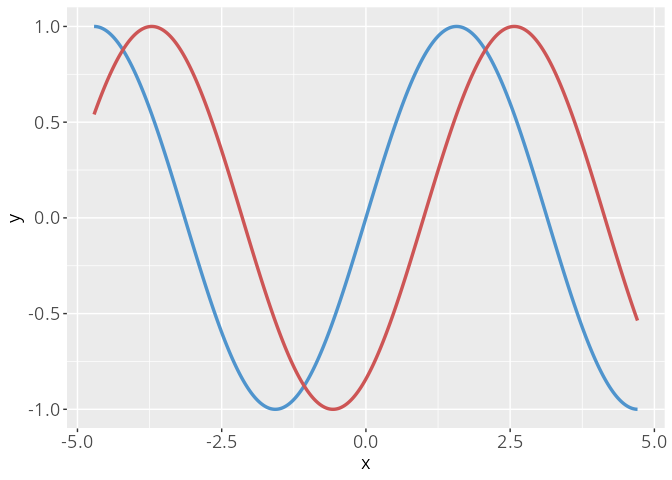
Verschiebung in x-Richtung
Eine Verschiebung in x Richtung um den Wert a \in \mathbb{R} erreichen wir durch die Zuordnung
\begin{align*} g(x) = f(x-a). \end{align*}
Ist a>0, so entspricht dies einer Verschiebung des Graphen nach rechts.
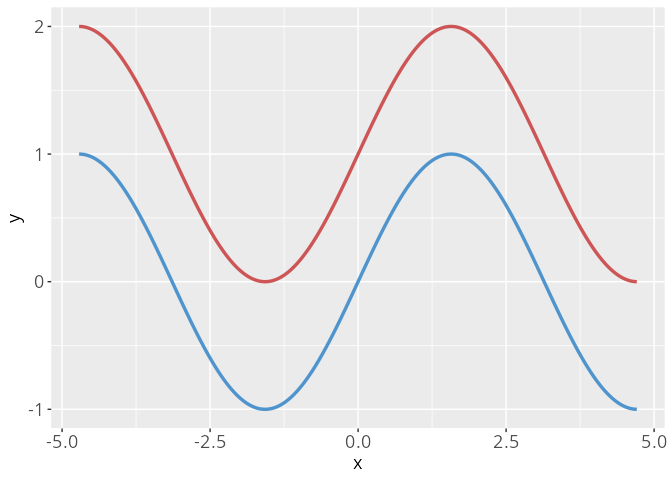
Verschiebung in y-Richtung
Die Verschiebung in y-Richtung ist durch die Addition einer Konstanten a \in \mathbb{R} zu erreichen
\begin{align*} g(x) = f(x)+a. \end{align*}
Ist die Konstante a>0, so entspricht dies einer Verschiebung nach oben, ist a<0 so entspricht dieser einer Verschiebung nach unten.
20.6.2 Spiegelungen
Spiegelung an der x-Achse
\begin{align*} g(x) = -f(x) \end{align*}
Spiegelung an der y-Achse
\begin{align*} g(x) = f(-x) \end{align*}
Beispiel
20.6.3 Streckungen / Stauchungen
Streckung / Stauchung in x-Richtung
\begin{align*} g(x) = f(ax) \end{align*}
Streckung / Stauchung in y-Richtung
\begin{align*} g(x) = af(x) \end{align*}
Falls a<0 ist, so handelt es sich offenbar nicht um eine einfache Streckung oder Stauchung, sondern um eine Streckspiegelung, da wir gleichzeitig an der x-Achse spiegeln.