19 Integration

Wir wollen uns in diesem Kapitel mit dem Riemann-Integration beschäftigen. Das Riemann-Integral ist eine Methode um Flächen zwsichen der x-Achse und dem Graphen einer Funktion zu bestimmen.

Es stellt sich heraus, dass die Integration die Umkehrung der Differentiation ist.

19.1 Ober- und Untersummen

Es gibt mehrere Möglichkeiten sich dem Integral einer Funktion zu nähern. Betrachten wir folgendes Problem. Gegeben ist eine Funktion f: I \to \mathbb{R}, die auf einem Intervall I \subset \mathbb{R} definiert ist. Nun wollen wir die Fläche bestimmen die von der Funktion f und der x-Achse in einem Intervall [a, b] \subseteq I eingeschlossen wird.

Idee

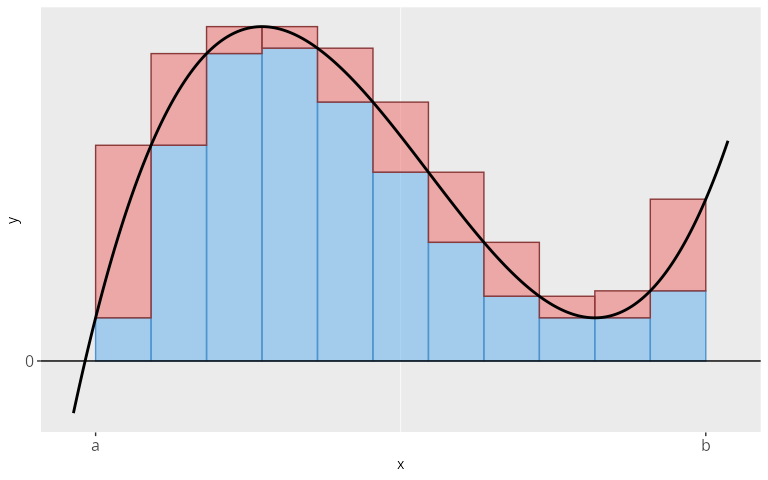
Die Idee ist die Fläche unter der Kurve durch zwei andere Flächen, der Obersumme S_n und der Untersumme s_n zu nähern. Dazu teilen wir das Intervall [a, b] in n gleich breite Segmente der Breite \Delta x = \frac{b-a}{n} ein. Dann werten wir die Funktion an den Stützstellen a, a + \Delta x, a + 2\Delta x, \cdots, a + n\Delta x = b aus und können so die Flächen der Rechtecke, wie sie in Abbildung 19.1 zu sehen sind, bestimmen.

Abbildung 19.1: Unter- und Obersumme für die Fläche unter einer Funktion. Während die Obersumme (rote + blaue Rechtecke) die Fläche unterhalb des Graphen überschätzen, unterschätzt die Untersumme (nur blaue Rechtecke) die Fläche unter dem Graphen.

Die Fläche F unter der Kurve kann nun durch eine Obersumme S_n, also die Summe der größeren Rechtecke (in den Grafiken rot und blau), nach oben abgeschätzt werden und durch eine Untersumme s_n, (in den Grafiken nur die blauen Rechtecke) nach unten. Es gilt S_n > F > s_n. Der Übersicht halber verzichten wir in der Notation auf die Grenzen a und b. In Abbildung 19.1 ist die Untersumme s_{11} (blaue Rechtecke) und die Obersumme S_{11} (blaue und rote Rechtecke) eingezeichnet.

In einer Formel kann man die Summen schreiben als

S_n = \sum_{i = 1}^{n} f(x_i^{\text{sup}}) \cdot \Delta x \qquad \text{und} \qquad s_n = \sum_{i = 1}^{n} f(x_i^{\text{inf}}) \cdot \Delta x. Dabei bezeichnen wir mit x_i^{\text{sup}} bzw. x_i^{\text{inf}} das Supremum bzw. Infimum des i. Intervalls.

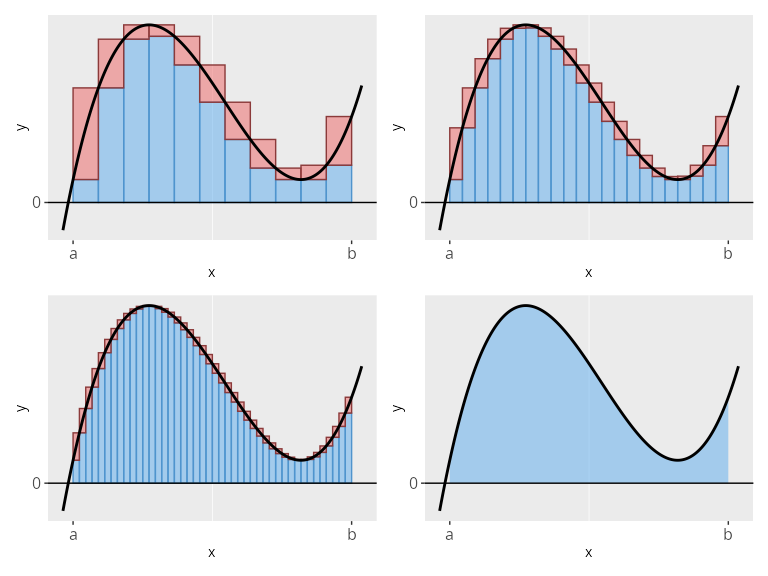
Abbildung 19.2: Verkleinert man die Breite der Rechtecke, so nähern sich Unter- und Obersumme einander an und approximieren die Fläche besser. Im Grenzwert erhält man den Flächeninhalt unter der Kurve.

Erhöht man nun die Anzahl der Intervalle, so nähern sich die Ober- und die Untersumme einander an und im Grenzwert n \to \infty sind beide Summen gleich und wir schreiben

\lim_{n \to \infty} s_n([a, b]) = \lim_{n \to \infty} S_n([a, b]) =: \int_{a}^{b} f(x)\,\mathrm{d}x.

Beispiel

Wir wollen die Fläche unter der Funktion f mit f(x) = x^2 im Intervall [a, b] berechnen. Im Fall einer monoton steigenden Funktion (das entspricht bei der obigen Funktion ein a \ge 0) ist das Infimum gleich der linken Grenze des Intervalls und das Supremum die rechte Grenze des Intervalls. Mit dieser kleinen Spezialisierung ergibt sich

\begin{aligned} S_n([a,b]) & = \Delta x \cdot \sum_{k=1}^n f(a + k\Delta x) \qquad (\text{mit} \; \Delta x = \frac{b-a}{n}) \\[2ex] & = \Delta x \cdot \sum_{k=1}^n \left((a + k\Delta x)^2 \right) \qquad (\text{mit} \; f(x) = x^2)\\[2ex] & = \Delta x \cdot \sum_{k=1}^n \left(a^2 + 2ak\Delta x + k^2\Delta x^2 \right) \\[2ex] & = \Delta x \cdot \underbrace{\sum_{k=1}^n a^2}_{= na^2} + \Delta x \cdot \underbrace{\sum_{k=1}^n 2ak\Delta x}_{= 2a\Delta x \sum_{k=1}^n k} + \Delta x \cdot \underbrace{\sum_{k=1}^n k^2\Delta x^2}_{\Delta x^2 \sum_{k=1}^{n} k^2} \\[2ex] & = \frac{b-a}{n}na^2 + \frac{b-a}{n} 2a\frac{b-a}{n} \frac{1}{2}n(n+1) + \frac{b-a}{n} \left(\frac{b-a}{n}\right)^2 \frac{1}{6}(2n+1)(n+1) \\ & = ba^2 - a^3 + 2ba - 2a^2 + \frac{2ba - 2a^2}{n} + \frac{b^3 - 3 b^2 a + 3 ba^2 - a^3}{n^3} \left( \frac{1}{6}(2n^3 + 3n^2 + n)\right) \\ & = ba^2 - a^3 + 2ba - 2a^2 + \frac{2ba - 2a^2}{n} + \frac{1}{3}b^3 -b^2 a + ba^2 -\frac{1}{3}a^3 + \frac{b^3 - 3b^2 a + 3ba^2 - a^3}{2n} \\ & \quad + \frac{b^3 - 3b^2 a + 3ba^2 - a^3}{6n^2} \\[2ex] & = \frac{1}{3} b^3 - \frac{1}{3} a^3 \\ & \quad + \frac{1}{n} \left(2ba - 2a^2 + \frac{1}{2}b^3 - \frac{3}{2}b^2 a + \frac{3}{2}ba^2 - \frac{1}{2}a^3\right) \\ & \quad + \frac{1}{n^2}\left(\frac{1}{6}b^3 - \frac{3}{6}b^2 a + \frac{3}{6}ba^2 - \frac{1}{6}a^3\right) \\[2ex] & = \frac{1}{3} b^3 - \frac{1}{3} a^3 + \mathcal{O}\left(\frac{1}{n}\right) + \mathcal{O}\left(\frac{1}{n^2}\right) \end{aligned}

Für die Untersumme ändert man in den Gleichungen oben lediglich die Summationsgrenzen. Statt von k = 1 bis n summieren wir über k=0 bis n-1. Es ergibt sich komplett analog zur Obersumme

s_n([a, b]) = \frac{1}{3} b^3 - \frac{1}{3} a^3 + \mathcal{O}\left(\frac{1}{n}\right) + \mathcal{O}\left(\frac{1}{n^2}\right).

Dabei ist \mathcal{O} das Landau Symbol. Dies bedeutet, dass die Terme von n abhängen und so skalieren wie das Argument in den Klammern angibt. Im obigen Fall haben wir zwei Terme, die für wachsende n gegen Null gehen. Dies bedeutet, dass

\lim_{n \to \infty} S_n([a, b]) = \lim_{n \to \infty} s_n([a, b]) = \frac{1}{3} (b^3 - a^3).

n	\Delta x	s_n	S_n	\frac{1}{2}(s_n+S_n)
1	1.000000	1.000000	4.000000	2.500000
2	0.500000	1.625000	3.125000	2.375000
4	0.250000	1.968750	2.718750	2.343750
8	0.125000	2.148438	2.523438	2.335938
16	0.067500	2.240234	2.427734	2.333984
32	0.033750	2.286621	2.380371	2.333496
64	0.016875	2.309937	2.356812	2.333374

19.2 Stammfunktion und unbestimmtes Integral

Die Integration ist die Umkehrung der Differentitaion. Gegeben ist also eine Funktion f mit dem Funktionsterm f(x) und gesucht ist eine Funktion F, so dass F'(x) = f(x). Offenbar ist diese Funktion nicht eindeutig, da additive Konstanten beim Differenzieren verschwinden

\begin{align*} (F(x) + c)' = F'(x) = f(x). \end{align*}

Definition: Stammfunktion

Sei I \subseteq{R} ein Intervall und f: I \to \mathbb{R} mit x \mapsto f(x) eine stetige Funktion auf dem Intervall I. Jede Funktion F für die gilt F'(x) = f(x) nennt man eine Stammfunktion von f.

Tabelle 19.1: Funktion f, maximaler Definitionsbereich D und Stammfunktion F für einige Funktionen.

Funktion f(x)		Stammfunktion F(x)
c	D = \mathbb{R}\; und \;c \in \mathbb{R}	cx + C
x^\alpha	D = \mathbb{R}\; und \;\alpha \in \mathbb{R} \setminus \{-1\}	\frac{1}{\alpha+1} \cdot x^{\alpha+1} + C
x^{-1}	D = \mathbb{R} \setminus \{0\}	\ln(\|x\|) + C
\mathsf{e}^x	D = \mathbb{R}	\mathsf{e}^x + C
a^x	D = \mathbb{R}\; und \;a \in \mathbb{R}_{>0} \setminus \{1\}	\frac{1}{\ln(a)} \cdot a^x + C
\sin(x)	D = \mathbb{R}	-\cos(x) + C
\cos(x)	D = \mathbb{R}	\sin(x) + C

19.3 Bestimmtes Integral

19.3.1 Grundlage

Fundamentalsatz der Analysis

Sei I \subseteq \mathbb{R} ein Intervall und die Funktion f: I \to \mathbb{R} eine stetige Funktion.

I. Existenz:

Für jedes c \in I ist die Funktion

\begin{align*} F: I \to \mathbb{R} \quad \text{mit} \quad F(x) = \int_{c}^x f(x)\,\mathrm{d}x \end{align*}

differenzierbar und eine Stammfunktion von f. Es gilt F'(x) = f(x).

II. Berechnung:

Seien a,b \in I, dann gilt die Newton-Leibniz-Formel

\begin{align*} \int_a^b f(x)\,\textrm{d}x = \left[F(x)\right]_{a}^{b} = F(x)\big|_{a}^{b} = F(b) - F(a). \end{align*}

Beispiel

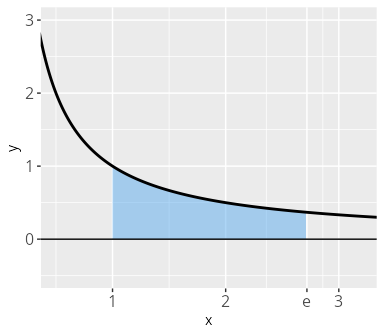
Wir wollen die Fläche unter der Funktion f: \mathbb{R} \setminus \{0\} \to \mathbb{R} mit f(x) = \frac{1}{x} im Intervall [1, \mathsf{e}] einschließt. Dazu berechnen wir

\begin{aligned} \int_{1}^{\mathsf{e}} \frac{1}{x}\,\mathrm{d}x & = \left[\ln(|x|)\right]_{1}^{\mathsf{e}} \\ & = \ln(\mathsf{e}) - \ln(1) \\ & = 1 \end{aligned}

Aus dem Teil II. des Fundamentalsatzes der Analysis folgt sofort der folgende Satz

Satz: Vertauschung der Grenzen

Vertauscht man die Ober- und Untergrenze eines bestimmten integrals, so ändert sich das Vorzeichen des Integrals:

\int_{a}^{b} f(x)\,\mathrm{d}x = -\int_{b}^{a} f(x)\,\mathrm{d}x.

Beweis

\begin{aligned} \int_{a}^{b} f(x)\,\mathrm{d}x & = F(b) - F(a) \\ & = -F(a) + F(b) \\ & = -(F(a) - F(b)) \\ & = -\int_{b}^{a} f(x)\,\mathrm{d}x \end{aligned}

19.3.2 Uneigentliche Integrale

Uneigentliche Integrale sind in zwei Fällen von Bedeutung:

Uneigentliche Integral 1. Art: Dieser Fall ist dann gegeben, wenn die Funktion über einen unbeschränkten Bereich integriert werden soll, also wenn mindestens eine der Grenzen gegen -\infty oder \infty geht.
Uneigentliche Integral 2. Art: In diesem Fall ist mindestens eine Grenze des Integrals kritisch ist. Dies bedeutet, dass die Funktion an der Grenze des Integrals eine Singularität hat und die Funktion selbst dort nicht definiert ist.

Beispiel 1

Wir wollen die Fläche berechnen, die von der Funktion f: \mathbb{R} \to \mathbb{R} mit f(x) = \mathsf{e}^{-x} und den beiden Achsen eingeschlossen wird. Dazu muss ein Integral bestimmt werdeb bei dem die obere Grenze gegen unendlich läuft.

\begin{aligned} \lim_{a \to \infty} \int_{0}^{a} \mathsf{e}^{-x}\,\mathrm{dx} & = \int_{0}^{\infty} \mathsf{e}^{-x}\,\mathrm{dx} \\ & = \left[-\mathsf{e}^{-x} \right]_{0}^{\infty} \\ & = 0 - (-\mathsf{e}^0) \\ & = 1 \end{aligned}

Beispiel 2

Im zweiten Beispiel ist die Grenze nicht im Definitionsbereich der Funktion:

\begin{aligned} \lim_{a \to 0+} \int_{a}^{1} \frac{1}{\sqrt{x}}\,\mathrm{d}x & = \int_{0}^{1} \frac{1}{\sqrt{x}}\,\mathrm{d}x \\ & = \int_{0}^{1} x^{-\frac{1}{2}}\,\mathrm{d}x \\ & = 2 \left[\frac{1}{-\frac{1}{2} + 1} x^{-\frac{1}{2} +1} \right]_0^{1} \\ & = \left[2x^{\frac{1}{2}}\right]_{0}^{1} \\ & = \left[2\sqrt{x} \right]_0^1 \\ & = 2 - 0 \\ & = 2 \end{aligned}

19.3.3 Übersicht

\int f(x)\, \mathrm{d}x \qquad \text{bzw.} \qquad \int_{a}^{b} f(x)\, \mathrm{d}x

Tabelle 19.2: In der Tabelle sind die Namen der Bestandteile eines Integralausdrucks aufgelistet.

Komponente	Name	Bedeutung
\int	Integralsymbol	Zeigt an, dass eine Integration durchgeführt wird.
a	Untere Grenze	Startpunkt des Integrationsintervalls (bei bestimmtem Integral).
b	Obere Grenze	Endpunkt des Integrationsintervalls (bei bestimmtem Integral).
f(x)	Integrand	Die zu integrierende Funktion.
x	Integrationsvariable	Variable, über die integriert wird.
\mathrm{d}x	Differentialelement	Gibt an, in Bezug auf welche Variable integriert wird.
\int f(x)\,\mathrm{d}x	Unbestimmtes Integral	Familie der Stammfunktionen von f(x).
\int_a^b f(x)\,\mathrm{d}x	Bestimmtes Integral	Zahl (Flächeninhalt unter der Kurve zwischen a und b).

19.4 Integrationsmethoden

Abbildung 19.3: Differentiation and Integration von xkcd

Leider treten Funktionen nicht immer in der elementaren Form, wie sie in Tabelle 19.1 aufgelistet sind, auf. Daher benötigen wir einige Regeln und Methoden um kompliziertere Integrale zu lösen. Wie der Comic ?fig-xkcd-DiffInt schon nahe liegt ist es in vielen Fällen schwierig bzw. unmöglich eine Stammfunktion, die aus elementaren Funktionen (das sind Polynome, Potenzfunktionen, Exponentialfunktionen, Logarithmen und trigonometrischen Funktionen) für eine gegebene Funktion zu finden.

Wir wollen mit ein paar grundlegenden Rechenregeln für Integrale anfangen, bevor wir uns zwei Methoden nähern um komplexere Integrale zu lösen.

Satz: Linearität des Integrals

Seien f und g zwei integrierbare Funktionen und seien \alpha, \beta \in \mathbb{R}, dann gilt:

\int \alpha f(x) + \beta g(x)\,\mathrm{d}x = \alpha \int f(x)\,\mathrm{d}x + \beta \int g(x)\,\mathrm{d}x.

Dieser Satz bedeutet zum einen, dass multiplikative Konstanten vor das Integral gezogen werden können und zum anderen, dass das Integral einer Summe, die Summe der Integrale ist.

Beispiel 1

Wenn wir eine Stammfunktion der Funktion f: \mathbb{R} \to \mathbb{R} mit f(x) = 5x^3 + 2x -6 suchen, dann können wir das Integral wie folgt berechnen:

\begin{aligned} F(x) & = \int f(x)\,\mathrm{d}x \\ & = \int 5x^3 + 2x - 6\,\mathrm{d}x \\ & = 5 \int x^3\,\mathrm{d}x + 2\int x\,\mathrm{d}x - 6 \int 1,\mathrm{d}x \\ & = 5 \frac{x^4}{4} + 2 \frac{x^2}{2} - 6 x + C \\ & = \frac{5}{4}x^4 + x^2 -6x + C \end{aligned}

Beispiel 2

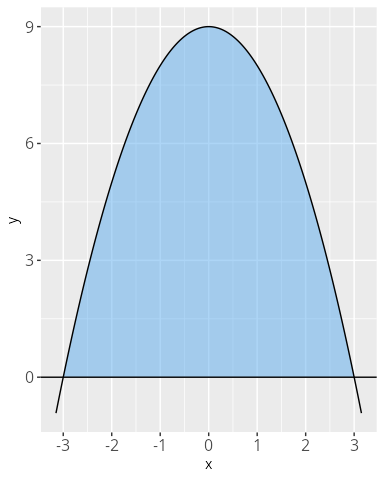
Man bestimme die Fläche die zwischen x-Achse und der Funktion f(x) = 9 - x^2 eingeschlossen wird. Die Funktion schneidet die x-Achse bei x_1=-3 und x_2=3. Daher müssen wir folgendes Integral bestimmen:

\begin{aligned} \int_{-3}^{3} 9-x^2\,\mathrm{d}x & = \left[9x-\frac{1}{3} x^3 \right]_{-3}^{3} \\ & = 2 \cdot \left[9x-\frac{1}{3} x^3 \right]_{0}^{3} \\ & = 2\cdot ((27 - 9) - (0 - 0)) \\ & = 36 \end{aligned}

Selbsttest

Gegeben ist die Funktion f mit

f(x) = - 2.8 x^3 - 2.1 x^2 + 2.8 x - 8.3

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(4) = -4.2 ist. Dann ist F(5) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 2.8 x^3 - 2.1 x^2 + 2.8 x - 8.3\,\mathrm{d}x \\ & = - \frac{2.8}{4} x^4 - \frac{2.1}{3} x^3 + \frac{2.8}{2} x^2 - 8.3 x + C \\ & = - 0.7 x^4 - 0.7 x^3 + 1.4 x^2 - 8.3 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = -4.2- F(4) \\ & = -300.9 \end{aligned}

C = -300.9

Gegeben ist die Funktion f mit

f(x) = - 2.8 x^3 - 3 x^2 + 5 x - 4.2

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(4) = 3.8 ist. Dann ist F(8) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 2.8 x^3 - 3 x^2 + 5 x - 4.2\,\mathrm{d}x \\ & = - \frac{2.8}{4} x^4 - \frac{3}{3} x^3 + \frac{5}{2} x^2 - 4.2 x + C \\ & = - 0.7 x^4 - 1 x^3 + 2.5 x^2 - 4.2 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = 3.8- F(4) \\ & = -3029 \end{aligned}

C = -3029

Gegeben ist die Funktion f mit

f(x) = 0.4 x^3 + 2.4 x^2 + 6.8 x + 6

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(3) = 5.3 ist. Dann ist F(5) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int 0.4 x^3 + 2.4 x^2 + 6.8 x + 6\,\mathrm{d}x \\ & = \frac{0.4}{4} x^4 + \frac{2.4}{3} x^3 + \frac{6.8}{2} x^2 + 6 x + C \\ & = 0.1 x^4 + 0.8 x^3 + 3.4 x^2 + 6 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = 5.3- F(3) \\ & = 204.5 \end{aligned}

C = 204.5

Gegeben ist die Funktion f mit

f(x) = - 0.8 x^3 - 4.8 x^2 - 1.2 x + 3.5

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(3) = -1.7 ist. Dann ist F(7) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 0.8 x^3 - 4.8 x^2 - 1.2 x + 3.5\,\mathrm{d}x \\ & = - \frac{0.8}{4} x^4 - \frac{4.8}{3} x^3 - \frac{1.2}{2} x^2 + 3.5 x + C \\ & = - 0.2 x^4 - 1.6 x^3 - 0.6 x^2 + 3.5 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = -1.7- F(3) \\ & = -981.3 \end{aligned}

C = -981.3

Gegeben ist die Funktion f mit

f(x) = - 3.2 x^3 - 3.3 x^2 - 6 x + 6.6

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(1) = 6.8 ist. Dann ist F(2) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 3.2 x^3 - 3.3 x^2 - 6 x + 6.6\,\mathrm{d}x \\ & = - \frac{3.2}{4} x^4 - \frac{3.3}{3} x^3 - \frac{6}{2} x^2 + 6.6 x + C \\ & = - 0.8 x^4 - 1.1 x^3 - 3 x^2 + 6.6 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = 6.8- F(1) \\ & = -15.3 \end{aligned}

C = -15.3

Gegeben ist die Funktion f mit

f(x) = - 0.8 x^3 + 2.4 x^2 - 3.6 x - 4.6

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(3) = 6.4 ist. Dann ist F(7) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 0.8 x^3 + 2.4 x^2 - 3.6 x - 4.6\,\mathrm{d}x \\ & = - \frac{0.8}{4} x^4 + \frac{2.4}{3} x^3 - \frac{3.6}{2} x^2 - 4.6 x + C \\ & = - 0.2 x^4 + 0.8 x^3 - 1.8 x^2 - 4.6 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = 6.4- F(3) \\ & = -295.2 \end{aligned}

C = -295.2

Gegeben ist die Funktion f mit

f(x) = - 2.8 x^3 - 1.8 x^2 + 7.8 x + 3.2

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(2) = 4.8 ist. Dann ist F(3) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 2.8 x^3 - 1.8 x^2 + 7.8 x + 3.2\,\mathrm{d}x \\ & = - \frac{2.8}{4} x^4 - \frac{1.8}{3} x^3 + \frac{7.8}{2} x^2 + 3.2 x + C \\ & = - 0.7 x^4 - 0.6 x^3 + 3.9 x^2 + 3.2 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = 4.8- F(2) \\ & = -29.4 \end{aligned}

C = -29.4

Gegeben ist die Funktion f mit

f(x) = 3.2 x^3 + 4.2 x^2 - 2.2 x + 9.2

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(5) = -3.2 ist. Dann ist F(7) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int 3.2 x^3 + 4.2 x^2 - 2.2 x + 9.2\,\mathrm{d}x \\ & = \frac{3.2}{4} x^4 + \frac{4.2}{3} x^3 - \frac{2.2}{2} x^2 + 9.2 x + C \\ & = 0.8 x^4 + 1.4 x^3 - 1.1 x^2 + 9.2 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = -3.2- F(5) \\ & = 1714.8 \end{aligned}

C = 1714.8

Gegeben ist die Funktion f mit

f(x) = 2.4 x^3 + 2.7 x^2 - 5.4 x + 7.7

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(4) = 0.7 ist. Dann ist F(8) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int 2.4 x^3 + 2.7 x^2 - 5.4 x + 7.7\,\mathrm{d}x \\ & = \frac{2.4}{4} x^4 + \frac{2.7}{3} x^3 - \frac{5.4}{2} x^2 + 7.7 x + C \\ & = 0.6 x^4 + 0.9 x^3 - 2.7 x^2 + 7.7 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = 0.7- F(4) \\ & = 2609.1 \end{aligned}

C = 2609.1

Gegeben ist die Funktion f mit

f(x) = - 3.2 x^3 + 4.2 x^2 + 7.8 x - 6

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(3) = -3.4 ist. Dann ist F(4) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 3.2 x^3 + 4.2 x^2 + 7.8 x - 6\,\mathrm{d}x \\ & = - \frac{3.2}{4} x^4 + \frac{4.2}{3} x^3 + \frac{7.8}{2} x^2 - 6 x + C \\ & = - 0.8 x^4 + 1.4 x^3 + 3.9 x^2 - 6 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = -3.4- F(3) \\ & = -70.3 \end{aligned}

C = -70.3

Gegeben ist die Funktion f mit

f(x) = 1.2 x^3 - 1.8 x^2 - 0.4 x + 7.6

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(-3) = 7.5 ist. Dann ist F(-1) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int 1.2 x^3 - 1.8 x^2 - 0.4 x + 7.6\,\mathrm{d}x \\ & = \frac{1.2}{4} x^4 - \frac{1.8}{3} x^3 - \frac{0.4}{2} x^2 + 7.6 x + C \\ & = 0.3 x^4 - 0.6 x^3 - 0.2 x^2 + 7.6 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = 7.5- F(-3) \\ & = -15.3 \end{aligned}

C = -15.3

Gegeben ist die Funktion f mit

f(x) = 2.8 x^3 + 1.8 x^2 + 7.8 x + 8

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(-3) = 7.5 ist. Dann ist F(4) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int 2.8 x^3 + 1.8 x^2 + 7.8 x + 8\,\mathrm{d}x \\ & = \frac{2.8}{4} x^4 + \frac{1.8}{3} x^3 + \frac{7.8}{2} x^2 + 8 x + C \\ & = 0.7 x^4 + 0.6 x^3 + 3.9 x^2 + 8 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = 7.5- F(-3) \\ & = 267.9 \end{aligned}

C = 267.9

Gegeben ist die Funktion f mit

f(x) = - 1.6 x^3 + 3.3 x^2 + 8.4 x + 11.6

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(-2) = 7.9 ist. Dann ist F(-1) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 1.6 x^3 + 3.3 x^2 + 8.4 x + 11.6\,\mathrm{d}x \\ & = - \frac{1.6}{4} x^4 + \frac{3.3}{3} x^3 + \frac{8.4}{2} x^2 + 11.6 x + C \\ & = - 0.4 x^4 + 1.1 x^3 + 4.2 x^2 + 11.6 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = 7.9- F(-2) \\ & = 20.6 \end{aligned}

C = 20.6

Gegeben ist die Funktion f mit

f(x) = 1.2 x^3 + 5.4 x^2 + 5.2 x + 10.2

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(0) = -4.4 ist. Dann ist F(1) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int 1.2 x^3 + 5.4 x^2 + 5.2 x + 10.2\,\mathrm{d}x \\ & = \frac{1.2}{4} x^4 + \frac{5.4}{3} x^3 + \frac{5.2}{2} x^2 + 10.2 x + C \\ & = 0.3 x^4 + 1.8 x^3 + 2.6 x^2 + 10.2 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = -4.4- F(0) \\ & = 10.5 \end{aligned}

C = 10.5

Gegeben ist die Funktion f mit

f(x) = - 0.4 x^3 - 0.3 x^2 + 1.8 x + 4.9

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(1) = -1.1 ist. Dann ist F(2) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 0.4 x^3 - 0.3 x^2 + 1.8 x + 4.9\,\mathrm{d}x \\ & = - \frac{0.4}{4} x^4 - \frac{0.3}{3} x^3 + \frac{1.8}{2} x^2 + 4.9 x + C \\ & = - 0.1 x^4 - 0.1 x^3 + 0.9 x^2 + 4.9 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = -1.1- F(1) \\ & = 4.3 \end{aligned}

C = 4.3

Gegeben ist die Funktion f mit

f(x) = - 3.2 x^3 + 1.2 x^2 + 5.4 x - 5.2

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(2) = 8.1 ist. Dann ist F(3) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 3.2 x^3 + 1.2 x^2 + 5.4 x - 5.2\,\mathrm{d}x \\ & = - \frac{3.2}{4} x^4 + \frac{1.2}{3} x^3 + \frac{5.4}{2} x^2 - 5.2 x + C \\ & = - 0.8 x^4 + 0.4 x^3 + 2.7 x^2 - 5.2 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = 8.1- F(2) \\ & = -28 \end{aligned}

C = -28

Gegeben ist die Funktion f mit

f(x) = 2.4 x^3 - 5.7 x^2 - 0.8 x - 3

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(1) = 4.9 ist. Dann ist F(5) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int 2.4 x^3 - 5.7 x^2 - 0.8 x - 3\,\mathrm{d}x \\ & = \frac{2.4}{4} x^4 - \frac{5.7}{3} x^3 - \frac{0.8}{2} x^2 - 3 x + C \\ & = 0.6 x^4 - 1.9 x^3 - 0.4 x^2 - 3 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = 4.9- F(1) \\ & = 122.1 \end{aligned}

C = 122.1

Gegeben ist die Funktion f mit

f(x) = - 3.2 x^3 - 3.9 x^2 - 9 x + 3.3

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(-1) = 8.5 ist. Dann ist F(3) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 3.2 x^3 - 3.9 x^2 - 9 x + 3.3\,\mathrm{d}x \\ & = - \frac{3.2}{4} x^4 - \frac{3.9}{3} x^3 - \frac{9}{2} x^2 + 3.3 x + C \\ & = - 0.8 x^4 - 1.3 x^3 - 4.5 x^2 + 3.3 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = 8.5- F(-1) \\ & = -114.7 \end{aligned}

C = -114.7

Gegeben ist die Funktion f mit

f(x) = 2 x^3 + 5.4 x^2 - 8.2 x - 6.9

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(3) = 6.8 ist. Dann ist F(5) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int 2 x^3 + 5.4 x^2 - 8.2 x - 6.9\,\mathrm{d}x \\ & = \frac{2}{4} x^4 + \frac{5.4}{3} x^3 - \frac{8.2}{2} x^2 - 6.9 x + C \\ & = 0.5 x^4 + 1.8 x^3 - 4.1 x^2 - 6.9 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = 6.8- F(3) \\ & = 375.8 \end{aligned}

C = 375.8

Gegeben ist die Funktion f mit

f(x) = 3.2 x^3 - 4.5 x^2 + 0.8 x - 8

Bestimmen Sie die Stammfunktion F der Funktion f derart, dass F(5) = 5 ist. Dann ist F(6) =

Damit ist das folgende Integral zu berechnen:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int 3.2 x^3 - 4.5 x^2 + 0.8 x - 8\,\mathrm{d}x \\ & = \frac{3.2}{4} x^4 - \frac{4.5}{3} x^3 + \frac{0.8}{2} x^2 - 8 x + C \\ & = 0.8 x^4 - 1.5 x^3 + 0.4 x^2 - 8 x + C \end{aligned}

Nun bestimmt man C mittels

\begin{aligned} C & = 5- F(5) \\ & = 401.7 \end{aligned}

C = 401.7

Gegeben ist die Funktion f mit

f(x) = - 0.8 x^3 - 0.9 x^2 - 0.6 x - 2.2

Bestimmen Sie \int\limits_{-3}^{5} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 0.8 x^3 - 0.9 x^2 - 0.6 x - 2.2\,\mathrm{d}x \\ & = - \frac{0.8}{4} x^4 - \frac{0.9}{3} x^3 - \frac{0.6}{2} x^2 - 2.2 x + C \\ & = - 0.2 x^4 - 0.3 x^3 - 0.3 x^2 - 2.2 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{-3}^{5} f(x)\,\mathrm{d}x & = F(5) - F(-3) \\ & = -176.8. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = - 1.6 x^3 - 3.9 x^2 + 7 x + 5.1

Bestimmen Sie \int\limits_{2}^{5} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 1.6 x^3 - 3.9 x^2 + 7 x + 5.1\,\mathrm{d}x \\ & = - \frac{1.6}{4} x^4 - \frac{3.9}{3} x^3 + \frac{7}{2} x^2 + 5.1 x + C \\ & = - 0.4 x^4 - 1.3 x^3 + 3.5 x^2 + 5.1 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{2}^{5} f(x)\,\mathrm{d}x & = F(5) - F(2) \\ & = -306.9. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = - 2.4 x^3 - 5.1 x^2 + 2.2 x - 9.5

Bestimmen Sie \int\limits_{-1}^{6} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 2.4 x^3 - 5.1 x^2 + 2.2 x - 9.5\,\mathrm{d}x \\ & = - \frac{2.4}{4} x^4 - \frac{5.1}{3} x^3 + \frac{2.2}{2} x^2 - 9.5 x + C \\ & = - 0.6 x^4 - 1.7 x^3 + 1.1 x^2 - 9.5 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{-1}^{6} f(x)\,\mathrm{d}x & = F(6) - F(-1) \\ & = -1173.9. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = - 2.8 x^3 - 0.6 x^2 + 4.6 x + 9.6

Bestimmen Sie \int\limits_{-3}^{5} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 2.8 x^3 - 0.6 x^2 + 4.6 x + 9.6\,\mathrm{d}x \\ & = - \frac{2.8}{4} x^4 - \frac{0.6}{3} x^3 + \frac{4.6}{2} x^2 + 9.6 x + C \\ & = - 0.7 x^4 - 0.2 x^3 + 2.3 x^2 + 9.6 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{-3}^{5} f(x)\,\mathrm{d}x & = F(5) - F(-3) \\ & = -297.6. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = - 2.8 x^3 + 5.1 x^2 - 2.4 x - 0.7

Bestimmen Sie \int\limits_{-2}^{5} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 2.8 x^3 + 5.1 x^2 - 2.4 x - 0.7\,\mathrm{d}x \\ & = - \frac{2.8}{4} x^4 + \frac{5.1}{3} x^3 - \frac{2.4}{2} x^2 - 0.7 x + C \\ & = - 0.7 x^4 + 1.7 x^3 - 1.2 x^2 - 0.7 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{-2}^{5} f(x)\,\mathrm{d}x & = F(5) - F(-2) \\ & = -230.3. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = - 3.2 x^3 + 2.4 x^2 - 4 x + 8.3

Bestimmen Sie \int\limits_{1}^{6} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 3.2 x^3 + 2.4 x^2 - 4 x + 8.3\,\mathrm{d}x \\ & = - \frac{3.2}{4} x^4 + \frac{2.4}{3} x^3 - \frac{4}{2} x^2 + 8.3 x + C \\ & = - 0.8 x^4 + 0.8 x^3 - 2 x^2 + 8.3 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{1}^{6} f(x)\,\mathrm{d}x & = F(6) - F(1) \\ & = -892.5. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = - 1.2 x^3 + 1.5 x^2 - 7.2 x + 0.5

Bestimmen Sie \int\limits_{-1}^{2} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 1.2 x^3 + 1.5 x^2 - 7.2 x + 0.5\,\mathrm{d}x \\ & = - \frac{1.2}{4} x^4 + \frac{1.5}{3} x^3 - \frac{7.2}{2} x^2 + 0.5 x + C \\ & = - 0.3 x^4 + 0.5 x^3 - 3.6 x^2 + 0.5 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{-1}^{2} f(x)\,\mathrm{d}x & = F(2) - F(-1) \\ & = -9.3. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = - 2.4 x^3 - 3.9 x^2 - 4 x - 5.1

Bestimmen Sie \int\limits_{-4}^{-2} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 2.4 x^3 - 3.9 x^2 - 4 x - 5.1\,\mathrm{d}x \\ & = - \frac{2.4}{4} x^4 - \frac{3.9}{3} x^3 - \frac{4}{2} x^2 - 5.1 x + C \\ & = - 0.6 x^4 - 1.3 x^3 - 2 x^2 - 5.1 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{-4}^{-2} f(x)\,\mathrm{d}x & = F(-2) - F(-4) \\ & = 85. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = 0.4 x^3 - 6 x^2 - 8.8 x - 2.7

Bestimmen Sie \int\limits_{3}^{6} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int 0.4 x^3 - 6 x^2 - 8.8 x - 2.7\,\mathrm{d}x \\ & = \frac{0.4}{4} x^4 - \frac{6}{3} x^3 - \frac{8.8}{2} x^2 - 2.7 x + C \\ & = 0.1 x^4 - 2 x^3 - 4.4 x^2 - 2.7 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{3}^{6} f(x)\,\mathrm{d}x & = F(6) - F(3) \\ & = -383.4. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = - 0.8 x^3 - 4.8 x^2 - 2.6 x + 10.4

Bestimmen Sie \int\limits_{-4}^{-2} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 0.8 x^3 - 4.8 x^2 - 2.6 x + 10.4\,\mathrm{d}x \\ & = - \frac{0.8}{4} x^4 - \frac{4.8}{3} x^3 - \frac{2.6}{2} x^2 + 10.4 x + C \\ & = - 0.2 x^4 - 1.6 x^3 - 1.3 x^2 + 10.4 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{-4}^{-2} f(x)\,\mathrm{d}x & = F(-2) - F(-4) \\ & = -5.2. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = - 3.2 x^3 - 5.7 x^2 + 7.4 x + 7.1

Bestimmen Sie \int\limits_{-1}^{7} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 3.2 x^3 - 5.7 x^2 + 7.4 x + 7.1\,\mathrm{d}x \\ & = - \frac{3.2}{4} x^4 - \frac{5.7}{3} x^3 + \frac{7.4}{2} x^2 + 7.1 x + C \\ & = - 0.8 x^4 - 1.9 x^3 + 3.7 x^2 + 7.1 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{-1}^{7} f(x)\,\mathrm{d}x & = F(7) - F(-1) \\ & = -2339.2. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = - 0.8 x^3 + 0.9 x^2 + 4 x - 5.6

Bestimmen Sie \int\limits_{-3}^{6} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 0.8 x^3 + 0.9 x^2 + 4 x - 5.6\,\mathrm{d}x \\ & = - \frac{0.8}{4} x^4 + \frac{0.9}{3} x^3 + \frac{4}{2} x^2 - 5.6 x + C \\ & = - 0.2 x^4 + 0.3 x^3 + 2 x^2 - 5.6 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{-3}^{6} f(x)\,\mathrm{d}x & = F(6) - F(-3) \\ & = -166.5. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = 1.6 x^3 - 1.5 x^2 - 4 x - 6.8

Bestimmen Sie \int\limits_{-2}^{3} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int 1.6 x^3 - 1.5 x^2 - 4 x - 6.8\,\mathrm{d}x \\ & = \frac{1.6}{4} x^4 - \frac{1.5}{3} x^3 - \frac{4}{2} x^2 - 6.8 x + C \\ & = 0.4 x^4 - 0.5 x^3 - 2 x^2 - 6.8 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{-2}^{3} f(x)\,\mathrm{d}x & = F(3) - F(-2) \\ & = -35.5. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = - 2 x^3 - 1.5 x^2 + 3 x - 7

Bestimmen Sie \int\limits_{-2}^{5} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 2 x^3 - 1.5 x^2 + 3 x - 7\,\mathrm{d}x \\ & = - \frac{2}{4} x^4 - \frac{1.5}{3} x^3 + \frac{3}{2} x^2 - 7 x + C \\ & = - 0.5 x^4 - 0.5 x^3 + 1.5 x^2 - 7 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{-2}^{5} f(x)\,\mathrm{d}x & = F(5) - F(-2) \\ & = -388.5. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = - 1.6 x^3 - 4.5 x^2 + 8.2 x + 10.5

Bestimmen Sie \int\limits_{-3}^{7} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 1.6 x^3 - 4.5 x^2 + 8.2 x + 10.5\,\mathrm{d}x \\ & = - \frac{1.6}{4} x^4 - \frac{4.5}{3} x^3 + \frac{8.2}{2} x^2 + 10.5 x + C \\ & = - 0.4 x^4 - 1.5 x^3 + 4.1 x^2 + 10.5 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{-3}^{7} f(x)\,\mathrm{d}x & = F(7) - F(-3) \\ & = -1214. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = 2 x^3 + 1.8 x^2 + 2.6 x - 11

Bestimmen Sie \int\limits_{-2}^{2} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int 2 x^3 + 1.8 x^2 + 2.6 x - 11\,\mathrm{d}x \\ & = \frac{2}{4} x^4 + \frac{1.8}{3} x^3 + \frac{2.6}{2} x^2 - 11 x + C \\ & = 0.5 x^4 + 0.6 x^3 + 1.3 x^2 - 11 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{-2}^{2} f(x)\,\mathrm{d}x & = F(2) - F(-2) \\ & = -34.4. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = 3.2 x^3 - 6 x^2 + 1.4 x + 6.8

Bestimmen Sie \int\limits_{3}^{7} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int 3.2 x^3 - 6 x^2 + 1.4 x + 6.8\,\mathrm{d}x \\ & = \frac{3.2}{4} x^4 - \frac{6}{3} x^3 + \frac{1.4}{2} x^2 + 6.8 x + C \\ & = 0.8 x^4 - 2 x^3 + 0.7 x^2 + 6.8 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{3}^{7} f(x)\,\mathrm{d}x & = F(7) - F(3) \\ & = 1279.2. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = 3.2 x^3 + 4.5 x^2 - 0.4 x + 11.8

Bestimmen Sie \int\limits_{0}^{5} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int 3.2 x^3 + 4.5 x^2 - 0.4 x + 11.8\,\mathrm{d}x \\ & = \frac{3.2}{4} x^4 + \frac{4.5}{3} x^3 - \frac{0.4}{2} x^2 + 11.8 x + C \\ & = 0.8 x^4 + 1.5 x^3 - 0.2 x^2 + 11.8 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{0}^{5} f(x)\,\mathrm{d}x & = F(5) - F(0) \\ & = 741.5. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = - 0.8 x^3 - 1.5 x^2 - 6.6 x + 12.6

Bestimmen Sie \int\limits_{1}^{5} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int - 0.8 x^3 - 1.5 x^2 - 6.6 x + 12.6\,\mathrm{d}x \\ & = - \frac{0.8}{4} x^4 - \frac{1.5}{3} x^3 - \frac{6.6}{2} x^2 + 12.6 x + C \\ & = - 0.2 x^4 - 0.5 x^3 - 3.3 x^2 + 12.6 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{1}^{5} f(x)\,\mathrm{d}x & = F(5) - F(1) \\ & = -215.6. \end{aligned}

Gegeben ist die Funktion f mit

f(x) = 3.2 x^3 + 5.1 x^2 - 0.8 x - 11.7

Bestimmen Sie \int\limits_{-4}^{5} f(x)\,\mathrm{d}x=

Wir bestimmen zuerst eine Stammfunktion:

\begin{aligned} F(x) &= \int f(x)\,\mathrm{d} x \\ & = \int 3.2 x^3 + 5.1 x^2 - 0.8 x - 11.7\,\mathrm{d}x \\ & = \frac{3.2}{4} x^4 + \frac{5.1}{3} x^3 - \frac{0.8}{2} x^2 - 11.7 x + C \\ & = 0.8 x^4 + 1.7 x^3 - 0.4 x^2 - 11.7 x + C \end{aligned}

Durch Einsetzen der Grenzen in das bestimmte Integral können wir den Wert des Integrals bestimmen. Es ergibt sich:

\begin{aligned} \int\limits_{-4}^{5} f(x)\,\mathrm{d}x & = F(5) - F(-4) \\ & = 507.6. \end{aligned}

Satz: Additivität

Sei eine Funktion f: I \to \mathbb{R} auf dem Intervall I \subseteq \mathbb{R} integrierbar, und a, b, c \in I, dann gilt:

\int_{a}^{c} f(x)\,\mathrm{d}x = \int_{a}^{b} f(x)\,\mathrm{d}x + \int_{b}^{c} f(x)\,\mathrm{d}x

Diese Formel ist für den Fall a < b < c sehr anschaulich, wie wir in Abbildung 19.4 leicht sehen können: die Gesamtfläche wird in zerlegt und offenbar ist die Gesamtfläche die Summe der beiden Einzelflächen.

Für den Fall, dass a < c < b ist können wir das Vorzeichen des zweiten Integrals durch Vertauschen der Grenzen ändern:

\begin{aligned} \int_{a}^{c} f(x)\,\mathrm{d}x & = \int_{a}^{b} f(x)\,\mathrm{d}x + \int_{b}^{c} f(x)\,\mathrm{d}x \\ & = \int_{a}^{b} f(x)\,\mathrm{d}x - \int_{c}^{b} f(x)\,\mathrm{d}x. \end{aligned} Dies bedeutet anschaulich, dass von der gesamten Fläche ein Teil abgezogen wird.

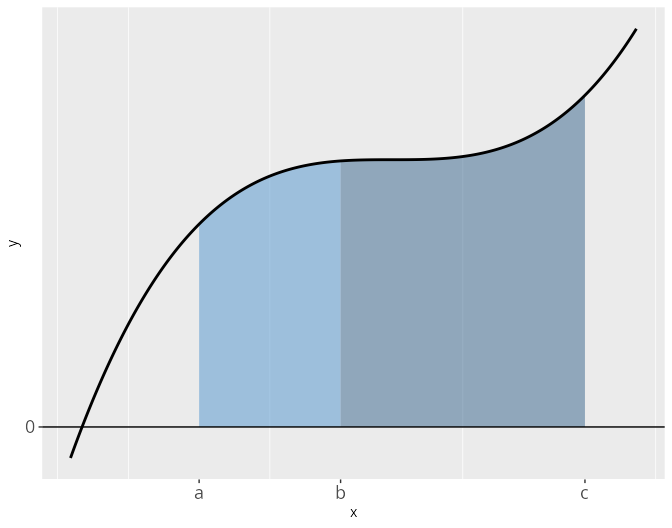
Abbildung 19.4: Die gesamt Fläche ist durch die Summe der beiden kleineren Fläche gegeben.

Die Additivität bei den bestimmten Integralen ist insbesondere dann nützlich, wenn eine Funktion Knicke hat oder unstetig ist. Dies können zum Beispiel Betragsfunktionen sein oder Funktionen, die nur abschnittsweise definiert sind.

Beispiel

Betrachten wir die Funktion f: \mathbb{R} \to \mathbb{R} mit

\begin{aligned} f(x) = \begin{cases} 1 \quad & : & \text{für} \quad 0 \le x \le 2 \\ x^2 + 4 & : & \text{für} \quad 2 < x \le 5 \\ 0 & : & \text{sonst}, \end{cases} \end{aligned}

und bestimmen das bestimmte Integral in den Grenzen von -2 bis 6:

\begin{aligned} \int_{-2}^6 f(x)\,\mathrm{d}x & = \underbrace{\int_{-2}^0 0\,\mathrm{d}x}_{=0} + \int_0^2 1\,\mathrm{d}x + \int_2^5 x^2 + 4 \,\mathrm{d}x + \underbrace{\int_{5}^6 0\,\mathrm{d}x}_{=0} \\ & = \left[x\right]_0^2 + \left[\frac{1}{3}x^3 + 4x\right]_2^5 \\ & = (2 - 0) + \left(\frac{1}{3}5^3 + 4\cdot 5 - \left(\frac{1}{3}2^3 + 4\cdot 2 \right) \right) \\ & = 53. \end{aligned}

19.4.1 Partielle Integration

Die partielle Integration ist die Umkehrung der Produktregel, die aus der Differentialrechnung bekannt ist.

Seien u' und v Funktionen von einer Variablen x, dann kann man die partielle Integration für ein bestimmtes Integral schreiben als

\begin{aligned} \int_a^b u'(x) \cdot v(x)\,\mathrm{d}x = \left[ u(x) \cdot v(x)\right]_{a}^{b} - \int_{a}^{b} u(x) \cdot v'(x)\,\mathrm{d}x \end{aligned}

Schreibt man die Ableitungen der Funtionen in der Form

\begin{aligned} u'(x) = \frac{\mathrm{d}u(x)}{\mathrm{d}x} \quad \text{bzw.} \quad v'(x) = \frac{\mathrm{d}v(x)}{\mathrm{d}x} \end{aligned}

und setzt diese in die obige Formel ein, so erhält man eine äquivalkente Schreibweise, die sich in vielen Büchern findet.

\begin{aligned} \int_a^b v\,\mathrm{d}u = \left[ u \cdot v\right]_{a}^{b} - \int_{a}^{b} u\,\mathrm{d}v, \end{aligned}

Dabei sind die Differentiale in unserem Fall \mathrm{d}u = u'(x)\,\mathrm{d}x und analog \mathrm{d}v = v'(x)\,\mathrm{d}x.

Der Vorteil dieser Schreibweise ist, dass sie unabhängig von der Integrationsvariablen (hier x) ist.

Beispiel 1

Gesucht ist eine Stammfunktion zur Funktion g(x) = x \cdot 2^x. Dies bedeutet wir müssen das Integral

\begin{aligned} \int g(x)\,\mathrm{d}x = \int x \cdot 2^x \mathrm{d}x \end{aligned}

lösen.

Die Frage, die sich nun stellt, ist welcher der beiden Terme aus denen g zusammengestzt ist, das u' und welcher das v ist. Die Idee ist, dass der Ausdruck im Integral auf der rechten Seite einfacher zu integrieren sein muss als das Integral auf der linken Seite. Wählen wir

\begin{aligned} u(x) = x \qquad \text{und} \qquad v'(x) = 2^x. \end{aligned}

Die Funktion u wird durch diese Wahl beim Ableiten zu einer Konstanten, Exponentialfunktionen aber beim Integrieren nur einen konstanten Faktor erhalten und damit nicht komplizierter werden. Damit wird das Integral auf der rechten Seite lösbar.

Mit u'(x) = 1 und v(x) = \frac{2^x}{\ln(2)} ergibt sich.

\begin{aligned} \int x \cdot 2^x\,\mathrm{d}x & = x \cdot \frac{2^x}{\ln(2)} - \int 1 \cdot \frac{2^x}{\ln(2)}\,\mathrm{d}x \\ & = x \cdot \frac{2^x}{\ln(2)} - \frac{2^x}{(\ln(2))^2} + C \\ & = \frac{2^x}{\ln(2)} \left( x - \frac{1}{\ln(2)} \right) + C \end{aligned}

Aufgabe zur partiellen Integration

Bestimmen Sie auf die gleiche Weise das Integral

\begin{aligned} \int x \cdot \textsf{e}^{-2x}\,\mathrm{d}x. \end{aligned}

Lösung

Man wählt analog zu oben u(x) = x und v'(x) = \textsf{e}^{-2x}, so ergibt sich u'(x) = 1 und v(x) = -\frac{1}{2} \textsf{e}^{-2x} und damit ergibt sich für das Integral

\begin{aligned} \int x \cdot \textsf{e}^{-2x}\,\mathrm{d}x & = x \cdot \left(-\frac{1}{2} \textsf{e}^{-2x}\right) - \int 1 \cdot \left(-\frac{1}{2} \textsf{e}^{-2x}\right)\,\mathrm{d}x \\ & = - x \cdot \frac{1}{2} \textsf{e}^{-2x} - \left(\frac{1}{4} \textsf{e}^{-2x}\right) + C\\ & = -\frac{1}{4}\textsf{e}^{-2x} \left(2x + 1\right) + C \end{aligned}

Spezialfälle Partielle Integration

Integrale der Form $$ g(x) (x),x, \end{align*} können immer mit Hilfe der partiellen Integration integriert werden. Dabei ist \textsf{Pol}(x) ein Polynom und g(x) entweder eine Exponentialfunktion der Form a^x (mit a \in \mathbb{R}_{>0} \setminus \{1\}) oder \sin(x) bzw. \cos(x). Für ein Polynom n. Grades muss die partielle Integration n mal wiederholt werden, da sich der Grad des Polynoms bei jeder Wiederholung um 1 verringert.

Beispiel 2

Betrachten wir das folgende Integral

\begin{aligned} \int x^2 \cdot \textsf{e}^{x}\,\mathrm{d}x. \end{aligned}

Nach der obigen Bemerkung wählen wir v(x) = x^2 und u'(x) = \textsf{e}^x. Damit ergibt sich mit v'(x) = 2x und u(x) = \textsf{e}^x

\begin{aligned} \int x^2 \cdot \textsf{e}^{x}\,\mathrm{d}x & = x^2 \cdot \textsf{e}^{x} - \int 2 x \cdot \textsf{e}^{x}\,\mathrm{d}x \\ & = x^2 \cdot \textsf{e}^{x} - \left(2x \cdot \textsf{e}^{x} - \int 2 \cdot \textsf{e}^{x}\,\mathrm{d}x\right) \\ & = x^2 \cdot \textsf{e}^{x} - 2x \cdot \textsf{e}^{x} + 2 \cdot \textsf{e}^{x} + C \\ & = \textsf{e}^{x}\left(x^2 - 2x + 2\right) + C \end{aligned}

Das im zu integrierenden Ausdruck vorkommende Polynom ist nach der ersten Integration nicht mehr vom Grad 2, sondern nur noch vom Grad 1. Wiederholen wir die partielle Integration ein weiteres Mal, so erhalten wir das Ergebnis.

Beispiel 3

Bei manchen Funktionen ist nicht offensichtlich, dass man die partielle Integration nutzen kann um die Stammfunktion zu bestimmen. Ein einfaches, aber sehr nützliches Beispiel ist die Integration des natürlichen Logarithmus. Da es sich erstmal nicht um ein Produkt handelt bedienen wir uns eines Kniffes und schreiben \int \ln(x)\,\mathrm{d}x = \int 1 \cdot \ln(x)\,\mathrm{d}x. Wir erhalten

\begin{aligned} \mathrm{d}u = 1 \mathrm{d}x \quad \implies \quad u = x \quad \text{und} \quad v = \ln(x) \quad \implies \quad \mathrm{d}v = \frac{1}{x} \mathrm{d}x \end{aligned}

\begin{aligned} \int \ln(x)\,\mathrm{d}x & = \int 1 \cdot \ln(x)\,\mathrm{d}x \\ & = x \cdot \ln(x) - \int x \cdot \frac{1}{x}\,\mathrm{d} x \\ & = x \cdot \ln(x) - x + C \\ & = x \cdot (\ln(x) -1) + C \end{aligned}

Aufgabe zur partiellen Integration

Bestimmen Sie auf analoge Weise das Integral

\begin{aligned} \int \frac{\ln(x)}{x^3}\,\mathrm{d}x. \end{aligned}

Lösung

Man wählt analog zu oben u(x) = \ln(x) und v'(x) = \frac{1}{x^{3}} = x^{-3}, so ergibt sich u'(x) = \frac{1}{x} und v(x) = -\frac{1}{2}x^{-2}. Damit kann man schreiben

\begin{aligned} \mathrm{d}u = \frac{1}{x}\,\mathrm{d}x, \qquad \text{und} \qquad \mathrm{d}v = \frac{1}{x^{3}}\,\mathrm{d}x \end{aligned}

\begin{aligned} \int \frac{\ln(x)}{x^3}\,\mathrm{d}x & = -\frac{1}{2}x^{-2}\cdot \ln(x) - \int \left(-\frac{1}{2}x^{-2} \cdot \frac{1}{x}\right)\,\mathrm{d}x \\ & = -\frac{1}{2} \frac{\ln(x)}{x^2} + \frac{1}{2} \int \frac{1}{x^3}\,\mathrm{d}x \\ & = -\frac{1}{2} \frac{\ln(x)}{x^2} - \frac{1}{4}\frac{1}{x^2} + C \\ & = -\frac{1}{4x^2}\left(2\ln(x) + 1 \right) + C \end{aligned}

19.4.2 Substitution

Die Substitution ist die Umkehrung der Kettenregel, die von der Differentiation bekannt sein sollte. Leitet man ein verkettete Funktion der Form f(g(x)) nach x ab, so erhält man g'(x) \cdot f'(g(x)). Aus diesem Grund schauen wir uns Integrale der folgenden Form an:

\begin{aligned} \int g'(x) f'(g(x)) \, \mathrm{d}x. \end{aligned}

Wir sehen, dass f und g verkettete Funktionen sind und – das ist der zweite wichtige Teil – die Ableitung der inneren Funktion, also g' außerhalb der geschatelten Funktionen stehen.

Beispiele

für Integrale, die mit Hilfe der Substitution gelöst werden können und von der obigen Form sind, wären zum Beispiel

\begin{aligned} \int 4 \mathsf{e}^{-2x}\,\mathrm{d}x. \end{aligned}

\begin{aligned} \int x^3 \sqrt{1+x^4} \,\mathrm{d}x. \end{aligned}

\begin{aligned} \int x \cdot \mathsf{e}^{ax^2} \,\mathrm{d}x. \end{aligned}

Vorgehensweise

Was machen wir nun, um eine derartige Aufgabe zu lösen?

Der erste Schritt besteht darin die den richtigen Term zu substituieren, das bedeutet eine neue Variable einzuführen. Da der Integrand von der Form g'(x)\cdot f'(g(x)) ist die Substitution: y = g(x). Eine einfache Ersetzung der Variablen reicht noch nicht aus, da das ursprüngliche Integral bezüglich x und nicht y integriert wird. Wir benöten also noch ein Differential \mathrm{d}y, das wir aus der Ableitung von y bezüglich x erhalten:

\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}x} = g'(x) \quad \text{oder} \quad \mathrm{d}x = \frac{1}{g'(x)} \,\mathrm{d}y. \end{aligned}

Setzen wir beides in das ursprüngliche Integral ein, erhalten wir

\begin{aligned} \int g'(x) f'(g(x)) \, \mathrm{d}x & = \int g'(x) f'(y) \frac{1}{g'(x)} \, \mathrm{d}y \\ & = \int f'(y) \, \mathrm{d}y \\ & = f(y) + C \\ & = f(g(x)) + C \end{aligned}

Somit haben sich die Terme, die außerhalb der Funktion f' weg und übrig bleibt die Aufgabe die äußere Funktion f' zu integrieren.

Nach der Integration müssen wir die Variablen resubstituieren. Das heißt wir setzen für y wieder g(x) ein.

Beispiel 1

Ein sehr einfaches Beispiel ist das folgende:

\begin{aligned} \int 4 \mathsf{e}^{-2x}\,\mathrm{d}x. \end{aligned}

Die verkettete Funktion ist \mathsf{e}^{-2x}, wobei y = -2x die innere Funktion ist. Damit ergibt sich

\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}x} = g'(x) = -2 \quad \text{oder} \quad \mathrm{d}x = -\frac{1}{2} \, \mathrm{d}y. \end{aligned}

\begin{aligned} \int 4 \mathsf{e}^{-2x}\,\mathrm{d}x & = \int 4 \mathsf{e}^{y}\cdot \left(-\frac{1}{2}\right) \,\mathrm{d}y \\ & = -2 \int \mathsf{e}^{y}\,\mathrm{d}y \\ & = -2 \mathsf{e}^{y} + C \\ & = -2 \mathsf{e}^{-2x} + C. \end{aligned}

Aufgabe zur Substitution

Bestimmen Sie auf die gleiche Weise die Integrale

\begin{aligned} \int \textsf{e}^{ax}\,\mathrm{d}x, \qquad \int \sin(ax)\,\mathrm{d}x \quad \text{und} \quad \int \cos(ax)\,\mathrm{d}x. \end{aligned}

Lösungen

Alle drei Aufgaben können mit der gleichen Substitution y = ax gelöst werden. Mit dem Differential \mathrm{d}x = \frac{1}{a} \mathrm{d}y ergeben sich die folgenden Stammfunktionen

\begin{aligned} \int \textsf{e}^{ax}\,\mathrm{d}x = \frac{1}{a}\textsf{e}^{ax} + C \end{aligned}

Und einmal ausführlich mit allen Schritten:

\begin{aligned} \int \sin(ax) \, \mathrm{d}x = \int \sin(y) \frac{\mathrm{d}y}{a} = \frac{1}{a} \int \sin(y) \, \mathrm{d}y = -\frac{1}{a} \cos(y) + C = -\frac{1}{a} \cos(ax) + C \end{aligned}

\begin{aligned} \int \cos(ax)\,\mathrm{d}x = \frac{1}{a} \sin(ax) + C \end{aligned}

Beispiel 2

Das zweite Beispiel ist nun schon ein wenig anspruchsvoller.

\begin{aligned} \int x^3 \sqrt{1+x^4} \,\mathrm{d}x. \end{aligned}

Was man noch recht leicht erkennen kann ist, dass \sqrt{1+x^4} eine Verkettung ist, und dass x^3 bis auf eine multiplikative Konstante die Ableitung von x^4 ist. Die Aufgabe ist ein weinig schwieriger als das erste Beispiel, weil das Substituieren nicht mehr eindeutig ist: Wir könnten y = x^4 oder y = 1+x^4 nehmen (die 1 verschwindet nach dem Ableiten). Besser ist die zweite Variante, da man nach der Substitution keine Summe unter der Wurzel steht.

\begin{aligned} y = 1 + x^4 \quad \implies \quad \frac{\mathrm{d}y}{\mathrm{d}x} = 3x^3 \quad \implies \quad \mathrm{d}x = \frac{1}{3x^3}\, \mathrm{d}y \end{aligned}

Einsetzen liefert:

\begin{aligned} \int x^3 \sqrt{1+x^4} \,\mathrm{d}x & = \int x^3 \sqrt{y} \frac{1}{3x^3}\,\mathrm{d}y \\ & = \frac{1}{3} \int \sqrt{y}\,\mathrm{d}y \\ & = \frac{1}{3} \int y^{\frac{1}{2}} \,\mathrm{d}y \\ & = \frac{1}{3} \frac{1}{\frac{1}{2} + 1} y^{\frac{1}{2} + 1} + C \\ & = \frac{2}{9} y^{\frac{3}{2}} + C \\ & = \frac{2}{9} \left(1 + x^4\right)^{\frac{3}{2}} + C. \end{aligned}

Was können wir aus dem obigen Beispiel noch mitnehmen?

Damit die Integration übersichtlicher wird, haben wir die multiplikative Konstante \frac{1}{3} vor das Integral gezogen.
Um Wurzeln zu integrieren schreibt man diese in der Potenzform.

Aufgabe zur Substitution

Bestimmen Sie auf die gleiche Weise das Integral

\begin{aligned} \int \mathsf{e}^{2x}(\mathsf{e}^{2x}+5)^{2025} \,\mathrm{d}x. \end{aligned}

Lösung

\begin{aligned} y = \mathsf{e}^{2x}+5 \quad \implies \quad \frac{\mathrm{d}y}{\mathrm{d}x} = 2\mathsf{e}^{2x} \quad \implies \quad \mathrm{d}x = \frac{1}{2\mathsf{e}^{2x}}\, \mathrm{d}y \end{aligned}

\begin{aligned} \int \mathsf{e}^{2x}(\mathsf{e}^{2x}+5)^{2025}\,\mathrm{d}x & = \mathsf{e}^{2x} y^{2025} \frac{1}{2\mathsf{e}^{2x}}\, \mathrm{d}y \\ & = \frac{1}{2} \int y^{2025}\,\mathrm{d}y \\ & = \frac{1}{2 \cdot 2026} y^{2026} + C \\ & = \frac{1}{4052} (\mathsf{e}^{2x}+5)^{2026} + C \end{aligned}

Beispiel 3

Ein weiteres wichtiges Bespiel für die Substitution ist das Beispiel f(x) = x \mathsf{e}^{ax^2}. Wir substituieren den Exponenten der Exponentialfunktion, da dessen Ableitung proportional zu dem x vor der Exponentialfunktion ist. Es ergibt sich damit:

\begin{aligned} y = ax^2 \quad \implies \quad \frac{\mathrm{d}y}{\mathrm{d}x} = 2ax \quad \implies \quad \mathrm{d}x = \frac{1}{2ax}\mathrm{d}y \end{aligned}

Damit ergibt sich für das integral

\begin{aligned} \int x \mathsf{e}^{ax^2} \, \mathrm{d}x & = \int \frac{1}{2ax} x \mathsf{e}^y \,\mathrm{d}y \\ & = \frac{1}{2a} \int \mathsf{e}^y \,\mathrm{d}y \\ & = \frac{1}{2a} \mathsf{e}^y + C \\ & = \frac{1}{2a} \mathsf{e}^{ax^2} + C. \\ \end{aligned}

Zum Abschluss des Kapitels zur Substitution wollen wir noch zwei Beispiele behandeln bei denen man nicht sofort erkennt, dass die Substitution das Mittel der Wahl ist.

Beispiel 4

Wir bestimmen die Stammfunktion zu

\begin{aligned} \int \tan(x) \,\mathrm{d}x. \end{aligned}

Um das Problem anzugehen schreibt man die Tangensfunktion um. Mit der Substitution

\begin{aligned} y = \cos(x) \quad \implies \quad \frac{\mathrm{d}y}{\mathrm{d}x} = -\sin(x) \quad \implies \quad \mathrm{d}x = -\frac{1}{\sin(x)}\mathrm{d}y \end{aligned}

ergibt sich

\begin{aligned} \int \tan(x) \, \mathrm{d}x & = \int \frac{\sin(x)}{\cos(x)} \, \mathrm{d}x \\ & = \int \frac{\sin(x)}{y} \cdot \frac{-1}{\sin(x)} \mathrm{d}y \\ & = \int \frac{-1}{y} \mathrm{d}y \\ & = - \ln(y) + C \\ & = - \ln(\cos(x)) + C. \\ \end{aligned}

Aufgabe zur Substitution

Bestimmen Sie auf die gleiche Weise das Integral

\begin{aligned} \int \cot(x)\,\mathrm{d}x. \end{aligned}

Lösung

\begin{aligned} y = \sin(x) \quad \implies \quad \frac{\mathrm{d}y}{\mathrm{d}x} = \cos(x) \quad \implies \quad \mathrm{d}x = \frac{1}{\cos(x)}\mathrm{d}y \end{aligned}

\begin{aligned} \int \cot(x) \, \mathrm{d}x & = \int \frac{\cos(x)}{\sin(x)} \, \mathrm{d}x \\ & = \int \frac{\cos(x)}{y} \cdot \frac{1}{\cos(x)} \mathrm{d}y \\ & = \int \frac{1}{y} \mathrm{d}y \\ & = \ln(y) + C \\ & = \ln(\sin(x)) + C. \\ \end{aligned}

Das letzte Beispiel ist ähnlich, allerdings noch ein wenig seltsamer, da man einen Term substituiert, der selbst nicht im ursprünglichen Ausdruck vorkommt.

Beispiel 5

Wir wollen folgendes Integral bestimmen

\begin{aligned} \int \sin^3(x) \,\mathrm{d}x. \end{aligned}

Die vielleicht überraschende Substitution ist:

\begin{aligned} y = \cos(x) \quad \implies \quad \frac{\mathrm{d}y}{\mathrm{d}x} = -\sin(x) \quad \mathrm{d}x = -\frac{1}{\sin(x)}\,\mathrm{d}y \end{aligned}

Wir nutzen den trigonometrischen Pythagoras \sin^2(x) + \cos^2(x) = 1 bzw. \sin^2(x) = 1 - \cos^2(x) und schreiben \sin^3(x) = \sin(x)(1-\cos^2(x)) und ersetzen das \mathrm{d}x. Damit ergibt sich

\begin{aligned} \int \sin^3(x) \, \mathrm{d}x & = \int \sin(x)(1-\cos^2(x)) \, \mathrm{d}x \\ & = \int \sin(x)(1-y^2) \cdot \frac{-1}{\sin(x)} \mathrm{d}y \\ & = \int (y^2 - 1) \, \mathrm{d}y \\ & = \frac{1}{3} y^3 - y + C \\ & = \frac{1}{3}\cos^3(x) - \cos(x) + C. \end{aligned}

Aufgabe zur Substitution

Bestimmen Sie auf die gleiche Weise das Integral

\begin{aligned} \int \cos^3(x)\,\mathrm{d}x. \end{aligned}

Lösung

19.5 Weitere Aufgaben

Ein Auto fährt ab dem Zeitpunkt t = 0 mit einer Geschwindigkeit

v(t) = 0.6 \cdot (12 t - t^2)

bis es wieder zum Stillstand kommt.

Nach welcher Zeit kommt das Auto zum Stillstand? t_{\text{max}} =

Welche Höchstgeschwindigkeit erreicht das Auto? v_{\text{max}} =

Welche Strecke legt das Auto während der gesamten Zeit zurück? s(t_{\text{max}}) =

Wie hoch ist die durchschnittliche Geschwindigkeit während der Fahrt? \overline{v}=

Der Funktionsgraph der Geschwindigkeit v(t) sieht wie folgt aus:

Der obige Term lässt sich Faktorisieren, so dass man beide Nullstellen erhält:

v(t) = 0.6 \cdot (12 t - t^2) = 0.6 \cdot t \cdot (12 - t) damit sind t=0 und t = 12 = t_{\text{max}} die beiden Nullstellen. Bei der zweiten Nullstelle kommt das Auto wieder zum Stillstand.

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 6 maximal. Um nun v_{\text{max}} zu bestimmen muss daher gelten

\begin{aligned} v_{\text{max}} & = 0.6 \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = 0.6 \cdot 6 \cdot (12 - 6) \\ & = 21.6 \end{aligned}

Die zurückgelegte Strecke ist eine Integration der Geschwindigkeit v über die Zeit t:

\begin{aligned} s(t_{\text{max}}) & = \int_{0}^{12} v(t)\,\mathrm{d}t \\ & = \int_{0}^{12} 7.2 \cdot t - 0.6 \cdot t^2\,\mathrm{d}t \\ & = \underbrace{3.6 \cdot 12^2 - 0.2 \cdot 12^3}_{\text{obere Grenze}} - \underbrace{(0 - 0)}_{\text{untere Grenze}} \\ & = 172.8 \end{aligned}

Grafisch kann man die zurückgelegte Strecke als den Flächeinhalt interpretieren, den die Parabel mit der t-Achse einschließt. Für die Durchschnittsgeschwindigkeit teilt man die zurückgelegte Strecke durch die Gesamtzeit der Fahrt. Es ergibt sich:

\overline{v} = \frac{s(12)}{12} = 14.4

Hier noch einmal alle Antworten mit den zugehörigen physikalischen Einheiten:

t_{\text{max}} = 12 in [s]
v_{\text{max}} = 21.6 in [m/s]
s(t_{\text{max}}) - s(0) = s(12) = 172.8 in [m]
\overline{v} = \frac{s(12)}{12} = 14.4 in [m/s]

Ein Auto fährt ab dem Zeitpunkt t = 0 mit einer Geschwindigkeit

v(t) = 1.92 \cdot (6 t - t^2)

bis es wieder zum Stillstand kommt.

Nach welcher Zeit kommt das Auto zum Stillstand? t_{\text{max}} =

Welche Höchstgeschwindigkeit erreicht das Auto? v_{\text{max}} =

Welche Strecke legt das Auto während der gesamten Zeit zurück? s(t_{\text{max}}) =

Wie hoch ist die durchschnittliche Geschwindigkeit während der Fahrt? \overline{v}=

Der Funktionsgraph der Geschwindigkeit v(t) sieht wie folgt aus:

Der obige Term lässt sich Faktorisieren, so dass man beide Nullstellen erhält:

v(t) = 1.92 \cdot (6 t - t^2) = 1.92 \cdot t \cdot (6 - t) damit sind t=0 und t = 6 = t_{\text{max}} die beiden Nullstellen. Bei der zweiten Nullstelle kommt das Auto wieder zum Stillstand.

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 3 maximal. Um nun v_{\text{max}} zu bestimmen muss daher gelten

\begin{aligned} v_{\text{max}} & = 1.92 \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = 1.92 \cdot 3 \cdot (6 - 3) \\ & = 17.28 \end{aligned}

Die zurückgelegte Strecke ist eine Integration der Geschwindigkeit v über die Zeit t:

\begin{aligned} s(t_{\text{max}}) & = \int_{0}^{6} v(t)\,\mathrm{d}t \\ & = \int_{0}^{6} 11.52 \cdot t - 1.92 \cdot t^2\,\mathrm{d}t \\ & = \underbrace{5.76 \cdot 6^2 - 0.64 \cdot 6^3}_{\text{obere Grenze}} - \underbrace{(0 - 0)}_{\text{untere Grenze}} \\ & = 69.12 \end{aligned}

\overline{v} = \frac{s(6)}{6} = 11.52

Hier noch einmal alle Antworten mit den zugehörigen physikalischen Einheiten:

t_{\text{max}} = 6 in [s]
v_{\text{max}} = 17.28 in [m/s]
s(t_{\text{max}}) - s(0) = s(6) = 69.12 in [m]
\overline{v} = \frac{s(6)}{6} = 11.52 in [m/s]

Ein Auto fährt ab dem Zeitpunkt t = 0 mit einer Geschwindigkeit

v(t) = 3 \cdot (6 t - t^2)

bis es wieder zum Stillstand kommt.

Nach welcher Zeit kommt das Auto zum Stillstand? t_{\text{max}} =

Welche Höchstgeschwindigkeit erreicht das Auto? v_{\text{max}} =

Welche Strecke legt das Auto während der gesamten Zeit zurück? s(t_{\text{max}}) =

Wie hoch ist die durchschnittliche Geschwindigkeit während der Fahrt? \overline{v}=

Der Funktionsgraph der Geschwindigkeit v(t) sieht wie folgt aus:

Der obige Term lässt sich Faktorisieren, so dass man beide Nullstellen erhält:

v(t) = 3 \cdot (6 t - t^2) = 3 \cdot t \cdot (6 - t) damit sind t=0 und t = 6 = t_{\text{max}} die beiden Nullstellen. Bei der zweiten Nullstelle kommt das Auto wieder zum Stillstand.

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 3 maximal. Um nun v_{\text{max}} zu bestimmen muss daher gelten

\begin{aligned} v_{\text{max}} & = 3 \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = 3 \cdot 3 \cdot (6 - 3) \\ & = 27 \end{aligned}

Die zurückgelegte Strecke ist eine Integration der Geschwindigkeit v über die Zeit t:

\begin{aligned} s(t_{\text{max}}) & = \int_{0}^{6} v(t)\,\mathrm{d}t \\ & = \int_{0}^{6} 18 \cdot t - 3 \cdot t^2\,\mathrm{d}t \\ & = \underbrace{9 \cdot 6^2 - 1 \cdot 6^3}_{\text{obere Grenze}} - \underbrace{(0 - 0)}_{\text{untere Grenze}} \\ & = 108 \end{aligned}

\overline{v} = \frac{s(6)}{6} = 18

Hier noch einmal alle Antworten mit den zugehörigen physikalischen Einheiten:

t_{\text{max}} = 6 in [s]
v_{\text{max}} = 27 in [m/s]
s(t_{\text{max}}) - s(0) = s(6) = 108 in [m]
\overline{v} = \frac{s(6)}{6} = 18 in [m/s]

Ein Auto fährt ab dem Zeitpunkt t = 0 mit einer Geschwindigkeit

v(t) = 2.94 \cdot (8 t - t^2)

bis es wieder zum Stillstand kommt.

Nach welcher Zeit kommt das Auto zum Stillstand? t_{\text{max}} =

Welche Höchstgeschwindigkeit erreicht das Auto? v_{\text{max}} =

Welche Strecke legt das Auto während der gesamten Zeit zurück? s(t_{\text{max}}) =

Wie hoch ist die durchschnittliche Geschwindigkeit während der Fahrt? \overline{v}=

Der Funktionsgraph der Geschwindigkeit v(t) sieht wie folgt aus:

Der obige Term lässt sich Faktorisieren, so dass man beide Nullstellen erhält:

v(t) = 2.94 \cdot (8 t - t^2) = 2.94 \cdot t \cdot (8 - t) damit sind t=0 und t = 8 = t_{\text{max}} die beiden Nullstellen. Bei der zweiten Nullstelle kommt das Auto wieder zum Stillstand.

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 4 maximal. Um nun v_{\text{max}} zu bestimmen muss daher gelten

\begin{aligned} v_{\text{max}} & = 2.94 \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = 2.94 \cdot 4 \cdot (8 - 4) \\ & = 47.04 \end{aligned}

Die zurückgelegte Strecke ist eine Integration der Geschwindigkeit v über die Zeit t:

\begin{aligned} s(t_{\text{max}}) & = \int_{0}^{8} v(t)\,\mathrm{d}t \\ & = \int_{0}^{8} 23.52 \cdot t - 2.94 \cdot t^2\,\mathrm{d}t \\ & = \underbrace{11.76 \cdot 8^2 - 0.98 \cdot 8^3}_{\text{obere Grenze}} - \underbrace{(0 - 0)}_{\text{untere Grenze}} \\ & = 250.88 \end{aligned}

\overline{v} = \frac{s(8)}{8} = 31.36

Hier noch einmal alle Antworten mit den zugehörigen physikalischen Einheiten:

t_{\text{max}} = 8 in [s]
v_{\text{max}} = 47.04 in [m/s]
s(t_{\text{max}}) - s(0) = s(8) = 250.88 in [m]
\overline{v} = \frac{s(8)}{8} = 31.36 in [m/s]

Ein Auto fährt ab dem Zeitpunkt t = 0 mit einer Geschwindigkeit

v(t) = 4.56 \cdot (4 t - t^2)

bis es wieder zum Stillstand kommt.

Nach welcher Zeit kommt das Auto zum Stillstand? t_{\text{max}} =

Welche Höchstgeschwindigkeit erreicht das Auto? v_{\text{max}} =

Welche Strecke legt das Auto während der gesamten Zeit zurück? s(t_{\text{max}}) =

Wie hoch ist die durchschnittliche Geschwindigkeit während der Fahrt? \overline{v}=

Der Funktionsgraph der Geschwindigkeit v(t) sieht wie folgt aus:

Der obige Term lässt sich Faktorisieren, so dass man beide Nullstellen erhält:

v(t) = 4.56 \cdot (4 t - t^2) = 4.56 \cdot t \cdot (4 - t) damit sind t=0 und t = 4 = t_{\text{max}} die beiden Nullstellen. Bei der zweiten Nullstelle kommt das Auto wieder zum Stillstand.

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 2 maximal. Um nun v_{\text{max}} zu bestimmen muss daher gelten

\begin{aligned} v_{\text{max}} & = 4.56 \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = 4.56 \cdot 2 \cdot (4 - 2) \\ & = 18.24 \end{aligned}

Die zurückgelegte Strecke ist eine Integration der Geschwindigkeit v über die Zeit t:

\begin{aligned} s(t_{\text{max}}) & = \int_{0}^{4} v(t)\,\mathrm{d}t \\ & = \int_{0}^{4} 18.24 \cdot t - 4.56 \cdot t^2\,\mathrm{d}t \\ & = \underbrace{9.12 \cdot 4^2 - 1.52 \cdot 4^3}_{\text{obere Grenze}} - \underbrace{(0 - 0)}_{\text{untere Grenze}} \\ & = 48.64 \end{aligned}

\overline{v} = \frac{s(4)}{4} = 12.16

Hier noch einmal alle Antworten mit den zugehörigen physikalischen Einheiten:

t_{\text{max}} = 4 in [s]
v_{\text{max}} = 18.24 in [m/s]
s(t_{\text{max}}) - s(0) = s(4) = 48.64 in [m]
\overline{v} = \frac{s(4)}{4} = 12.16 in [m/s]

Ein Auto fährt ab dem Zeitpunkt t = 0 mit einer Geschwindigkeit

v(t) = 2.7 \cdot (8 t - t^2)

bis es wieder zum Stillstand kommt.

Nach welcher Zeit kommt das Auto zum Stillstand? t_{\text{max}} =

Welche Höchstgeschwindigkeit erreicht das Auto? v_{\text{max}} =

Welche Strecke legt das Auto während der gesamten Zeit zurück? s(t_{\text{max}}) =

Wie hoch ist die durchschnittliche Geschwindigkeit während der Fahrt? \overline{v}=

Der Funktionsgraph der Geschwindigkeit v(t) sieht wie folgt aus:

Der obige Term lässt sich Faktorisieren, so dass man beide Nullstellen erhält:

v(t) = 2.7 \cdot (8 t - t^2) = 2.7 \cdot t \cdot (8 - t) damit sind t=0 und t = 8 = t_{\text{max}} die beiden Nullstellen. Bei der zweiten Nullstelle kommt das Auto wieder zum Stillstand.

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 4 maximal. Um nun v_{\text{max}} zu bestimmen muss daher gelten

\begin{aligned} v_{\text{max}} & = 2.7 \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = 2.7 \cdot 4 \cdot (8 - 4) \\ & = 43.2 \end{aligned}

Die zurückgelegte Strecke ist eine Integration der Geschwindigkeit v über die Zeit t:

\begin{aligned} s(t_{\text{max}}) & = \int_{0}^{8} v(t)\,\mathrm{d}t \\ & = \int_{0}^{8} 21.6 \cdot t - 2.7 \cdot t^2\,\mathrm{d}t \\ & = \underbrace{10.8 \cdot 8^2 - 0.9 \cdot 8^3}_{\text{obere Grenze}} - \underbrace{(0 - 0)}_{\text{untere Grenze}} \\ & = 230.4 \end{aligned}

\overline{v} = \frac{s(8)}{8} = 28.8

Hier noch einmal alle Antworten mit den zugehörigen physikalischen Einheiten:

t_{\text{max}} = 8 in [s]
v_{\text{max}} = 43.2 in [m/s]
s(t_{\text{max}}) - s(0) = s(8) = 230.4 in [m]
\overline{v} = \frac{s(8)}{8} = 28.8 in [m/s]

Ein Auto fährt ab dem Zeitpunkt t = 0 mit einer Geschwindigkeit

v(t) = 2.94 \cdot (4 t - t^2)

bis es wieder zum Stillstand kommt.

Nach welcher Zeit kommt das Auto zum Stillstand? t_{\text{max}} =

Welche Höchstgeschwindigkeit erreicht das Auto? v_{\text{max}} =

Welche Strecke legt das Auto während der gesamten Zeit zurück? s(t_{\text{max}}) =

Wie hoch ist die durchschnittliche Geschwindigkeit während der Fahrt? \overline{v}=

Der Funktionsgraph der Geschwindigkeit v(t) sieht wie folgt aus:

Der obige Term lässt sich Faktorisieren, so dass man beide Nullstellen erhält:

v(t) = 2.94 \cdot (4 t - t^2) = 2.94 \cdot t \cdot (4 - t) damit sind t=0 und t = 4 = t_{\text{max}} die beiden Nullstellen. Bei der zweiten Nullstelle kommt das Auto wieder zum Stillstand.

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 2 maximal. Um nun v_{\text{max}} zu bestimmen muss daher gelten

\begin{aligned} v_{\text{max}} & = 2.94 \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = 2.94 \cdot 2 \cdot (4 - 2) \\ & = 11.76 \end{aligned}

Die zurückgelegte Strecke ist eine Integration der Geschwindigkeit v über die Zeit t:

\begin{aligned} s(t_{\text{max}}) & = \int_{0}^{4} v(t)\,\mathrm{d}t \\ & = \int_{0}^{4} 11.76 \cdot t - 2.94 \cdot t^2\,\mathrm{d}t \\ & = \underbrace{5.88 \cdot 4^2 - 0.98 \cdot 4^3}_{\text{obere Grenze}} - \underbrace{(0 - 0)}_{\text{untere Grenze}} \\ & = 31.36 \end{aligned}

\overline{v} = \frac{s(4)}{4} = 7.84

Hier noch einmal alle Antworten mit den zugehörigen physikalischen Einheiten:

t_{\text{max}} = 4 in [s]
v_{\text{max}} = 11.76 in [m/s]
s(t_{\text{max}}) - s(0) = s(4) = 31.36 in [m]
\overline{v} = \frac{s(4)}{4} = 7.84 in [m/s]

Ein Auto fährt ab dem Zeitpunkt t = 0 mit einer Geschwindigkeit

v(t) = 8.04 \cdot (4 t - t^2)

bis es wieder zum Stillstand kommt.

Nach welcher Zeit kommt das Auto zum Stillstand? t_{\text{max}} =

Welche Höchstgeschwindigkeit erreicht das Auto? v_{\text{max}} =

Welche Strecke legt das Auto während der gesamten Zeit zurück? s(t_{\text{max}}) =

Wie hoch ist die durchschnittliche Geschwindigkeit während der Fahrt? \overline{v}=

Der Funktionsgraph der Geschwindigkeit v(t) sieht wie folgt aus:

Der obige Term lässt sich Faktorisieren, so dass man beide Nullstellen erhält:

v(t) = 8.04 \cdot (4 t - t^2) = 8.04 \cdot t \cdot (4 - t) damit sind t=0 und t = 4 = t_{\text{max}} die beiden Nullstellen. Bei der zweiten Nullstelle kommt das Auto wieder zum Stillstand.

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 2 maximal. Um nun v_{\text{max}} zu bestimmen muss daher gelten

\begin{aligned} v_{\text{max}} & = 8.04 \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = 8.04 \cdot 2 \cdot (4 - 2) \\ & = 32.16 \end{aligned}

Die zurückgelegte Strecke ist eine Integration der Geschwindigkeit v über die Zeit t:

\begin{aligned} s(t_{\text{max}}) & = \int_{0}^{4} v(t)\,\mathrm{d}t \\ & = \int_{0}^{4} 32.16 \cdot t - 8.04 \cdot t^2\,\mathrm{d}t \\ & = \underbrace{16.08 \cdot 4^2 - 2.68 \cdot 4^3}_{\text{obere Grenze}} - \underbrace{(0 - 0)}_{\text{untere Grenze}} \\ & = 85.76 \end{aligned}

\overline{v} = \frac{s(4)}{4} = 21.44

Hier noch einmal alle Antworten mit den zugehörigen physikalischen Einheiten:

t_{\text{max}} = 4 in [s]
v_{\text{max}} = 32.16 in [m/s]
s(t_{\text{max}}) - s(0) = s(4) = 85.76 in [m]
\overline{v} = \frac{s(4)}{4} = 21.44 in [m/s]

Ein Auto fährt ab dem Zeitpunkt t = 0 mit einer Geschwindigkeit

v(t) = 3.24 \cdot (4 t - t^2)

bis es wieder zum Stillstand kommt.

Nach welcher Zeit kommt das Auto zum Stillstand? t_{\text{max}} =

Welche Höchstgeschwindigkeit erreicht das Auto? v_{\text{max}} =

Welche Strecke legt das Auto während der gesamten Zeit zurück? s(t_{\text{max}}) =

Wie hoch ist die durchschnittliche Geschwindigkeit während der Fahrt? \overline{v}=

Der Funktionsgraph der Geschwindigkeit v(t) sieht wie folgt aus:

Der obige Term lässt sich Faktorisieren, so dass man beide Nullstellen erhält:

v(t) = 3.24 \cdot (4 t - t^2) = 3.24 \cdot t \cdot (4 - t) damit sind t=0 und t = 4 = t_{\text{max}} die beiden Nullstellen. Bei der zweiten Nullstelle kommt das Auto wieder zum Stillstand.

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 2 maximal. Um nun v_{\text{max}} zu bestimmen muss daher gelten

\begin{aligned} v_{\text{max}} & = 3.24 \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = 3.24 \cdot 2 \cdot (4 - 2) \\ & = 12.96 \end{aligned}

Die zurückgelegte Strecke ist eine Integration der Geschwindigkeit v über die Zeit t:

\begin{aligned} s(t_{\text{max}}) & = \int_{0}^{4} v(t)\,\mathrm{d}t \\ & = \int_{0}^{4} 12.96 \cdot t - 3.24 \cdot t^2\,\mathrm{d}t \\ & = \underbrace{6.48 \cdot 4^2 - 1.08 \cdot 4^3}_{\text{obere Grenze}} - \underbrace{(0 - 0)}_{\text{untere Grenze}} \\ & = 34.56 \end{aligned}

\overline{v} = \frac{s(4)}{4} = 8.64

Hier noch einmal alle Antworten mit den zugehörigen physikalischen Einheiten:

t_{\text{max}} = 4 in [s]
v_{\text{max}} = 12.96 in [m/s]
s(t_{\text{max}}) - s(0) = s(4) = 34.56 in [m]
\overline{v} = \frac{s(4)}{4} = 8.64 in [m/s]

Ein Auto fährt ab dem Zeitpunkt t = 0 mit einer Geschwindigkeit

v(t) = 0.42 \cdot (16 t - t^2)

bis es wieder zum Stillstand kommt.

Nach welcher Zeit kommt das Auto zum Stillstand? t_{\text{max}} =

Welche Höchstgeschwindigkeit erreicht das Auto? v_{\text{max}} =

Welche Strecke legt das Auto während der gesamten Zeit zurück? s(t_{\text{max}}) =

Wie hoch ist die durchschnittliche Geschwindigkeit während der Fahrt? \overline{v}=

Der Funktionsgraph der Geschwindigkeit v(t) sieht wie folgt aus:

Der obige Term lässt sich Faktorisieren, so dass man beide Nullstellen erhält:

v(t) = 0.42 \cdot (16 t - t^2) = 0.42 \cdot t \cdot (16 - t) damit sind t=0 und t = 16 = t_{\text{max}} die beiden Nullstellen. Bei der zweiten Nullstelle kommt das Auto wieder zum Stillstand.

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 8 maximal. Um nun v_{\text{max}} zu bestimmen muss daher gelten

\begin{aligned} v_{\text{max}} & = 0.42 \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = 0.42 \cdot 8 \cdot (16 - 8) \\ & = 26.88 \end{aligned}

Die zurückgelegte Strecke ist eine Integration der Geschwindigkeit v über die Zeit t:

\begin{aligned} s(t_{\text{max}}) & = \int_{0}^{16} v(t)\,\mathrm{d}t \\ & = \int_{0}^{16} 6.72 \cdot t - 0.42 \cdot t^2\,\mathrm{d}t \\ & = \underbrace{3.36 \cdot 16^2 - 0.14 \cdot 16^3}_{\text{obere Grenze}} - \underbrace{(0 - 0)}_{\text{untere Grenze}} \\ & = 286.72 \end{aligned}

\overline{v} = \frac{s(16)}{16} = 17.92

Hier noch einmal alle Antworten mit den zugehörigen physikalischen Einheiten:

t_{\text{max}} = 16 in [s]
v_{\text{max}} = 26.88 in [m/s]
s(t_{\text{max}}) - s(0) = s(16) = 286.72 in [m]
\overline{v} = \frac{s(16)}{16} = 17.92 in [m/s]

Im folgenden Diagramm ist das Geschwindigkeits-Zeit-Diagramm eines Gefährts abgebildet. Der Graph der Funktion ist eine nach unten offene Parabel der Form

v(t) = A \cdot t \cdot (t_{\text{max}} -t) \qquad \text{mit} \qquad t_{\text{max}} = 4.

Die maximal erreichte Geschwindigkeit ist v_{\text{max}} = 37.68.

Bei allen Aufgabenteilen sind nur die Zahlen auf mindestens zwei Nachkommastellen genau anzugeben, keine Einheiten!

Bestimmen Sie den Parameter A =

Welche Strecke (in m) legt das Gefährt während der gesamten 4 Sekunden zurück? s(4) =

Wie hoch ist die durchschnittliche Geschwindigkeit (in m/s)? \overline{v}=

Welchen Anteil (in Prozent) der gesamten Strecke legt das Gefährt zwischen t = 1.1 und t= 2.7 zurück?

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 2 maximal. Um nun A zu bestimmen muss daher gelten

\begin{aligned} 37.68 & = A \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = A \cdot 2 \cdot (4 - 2) \end{aligned}

Löst man diesen Ausdruck nach A auf, so ergibt sich: A = 9.42.

Da die nächsten Aufgabenteile alle eine Integration von v benötigen, bestimmen wir s(T). Dies entspricht der zum Zeitpunkt T zurückgelegten Strecke:

\begin{aligned} s(T) & = \int_{0}^T v(t)\,\mathrm{d}t \\ & = \int_{0}^T 9.42 \cdot t \cdot (4 - t)\,\mathrm{d}t\\ & = \int_{0}^T 37.68 \cdot t - 9.42 \cdot t^2\,\mathrm{d}t \\ & = 18.84 \cdot T^2 - 3.14 \cdot T^3 \end{aligned} Die untere Grenze ist identisch 0, daher wurde diese im letzten Schritt gleich weggelassen. Damit kann man nun die restlichen Aufgaben lösen:

\begin{aligned} s(t_{\text{max}}) = s(4) & = 18.84 \cdot 4^2 - 3.14 \cdot 4^3 \\ & = 100.48 \end{aligned} Für die Durchschnittsgeschwindigkeit teilt man die zurückgelegte Strecke durch die Gesamtzeit der Fahrt. Es ergibt sich:

\overline{v} = \frac{s(4)}{4} = 25.12 Der Anteil, bestimmt man indem man die im Zeitintervall 1.1 bis 2.7 zurückgelegte Strecke durch die gesamte Strecke teilt. Es ergibt sich:

\begin{aligned} p = \frac{\int_{1.1}^{2.7} v(t)\,\mathrm{d}t}{\int_{0}^{4} v(t)\,\mathrm{d}t} & = \frac{s(2.7) - s(1.1)}{s(4) - s(0)} \\ & = \frac{75.53898 - 18.61706}{100.48 - 0} \\ & = 0.5665 \end{aligned}

Dies sind 56.65 Prozent.

A = 9.42
s(4) = 100.48
\overline{v} = 25.12
p = 56.65\%

Im folgenden Diagramm ist das Geschwindigkeits-Zeit-Diagramm eines Gefährts abgebildet. Der Graph der Funktion ist eine nach unten offene Parabel der Form

v(t) = A \cdot t \cdot (t_{\text{max}} -t) \qquad \text{mit} \qquad t_{\text{max}} = 4.

Die maximal erreichte Geschwindigkeit ist v_{\text{max}} = 10.8.

Bei allen Aufgabenteilen sind nur die Zahlen auf mindestens zwei Nachkommastellen genau anzugeben, keine Einheiten!

Bestimmen Sie den Parameter A =

Welche Strecke (in m) legt das Gefährt während der gesamten 4 Sekunden zurück? s(4) =

Wie hoch ist die durchschnittliche Geschwindigkeit (in m/s)? \overline{v}=

Welchen Anteil (in Prozent) der gesamten Strecke legt das Gefährt zwischen t = 1.2 und t= 3.2 zurück?

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 2 maximal. Um nun A zu bestimmen muss daher gelten

\begin{aligned} 10.8 & = A \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = A \cdot 2 \cdot (4 - 2) \end{aligned}

Löst man diesen Ausdruck nach A auf, so ergibt sich: A = 2.7.

Da die nächsten Aufgabenteile alle eine Integration von v benötigen, bestimmen wir s(T). Dies entspricht der zum Zeitpunkt T zurückgelegten Strecke:

\begin{aligned} s(T) & = \int_{0}^T v(t)\,\mathrm{d}t \\ & = \int_{0}^T 2.7 \cdot t \cdot (4 - t)\,\mathrm{d}t\\ & = \int_{0}^T 10.8 \cdot t - 2.7 \cdot t^2\,\mathrm{d}t \\ & = 5.4 \cdot T^2 - 0.9 \cdot T^3 \end{aligned} Die untere Grenze ist identisch 0, daher wurde diese im letzten Schritt gleich weggelassen. Damit kann man nun die restlichen Aufgaben lösen:

\begin{aligned} s(t_{\text{max}}) = s(4) & = 5.4 \cdot 4^2 - 0.9 \cdot 4^3 \\ & = 28.8 \end{aligned} Für die Durchschnittsgeschwindigkeit teilt man die zurückgelegte Strecke durch die Gesamtzeit der Fahrt. Es ergibt sich:

\overline{v} = \frac{s(4)}{4} = 7.2 Der Anteil, bestimmt man indem man die im Zeitintervall 1.2 bis 3.2 zurückgelegte Strecke durch die gesamte Strecke teilt. Es ergibt sich:

\begin{aligned} p = \frac{\int_{1.2}^{3.2} v(t)\,\mathrm{d}t}{\int_{0}^{4} v(t)\,\mathrm{d}t} & = \frac{s(3.2) - s(1.2)}{s(4) - s(0)} \\ & = \frac{25.8048 - 6.2208}{28.8 - 0} \\ & = 0.68 \end{aligned}

Dies sind 68 Prozent.

A = 2.7
s(4) = 28.8
\overline{v} = 7.2
p = 68\%

Im folgenden Diagramm ist das Geschwindigkeits-Zeit-Diagramm eines Gefährts abgebildet. Der Graph der Funktion ist eine nach unten offene Parabel der Form

v(t) = A \cdot t \cdot (t_{\text{max}} -t) \qquad \text{mit} \qquad t_{\text{max}} = 14.

Die maximal erreichte Geschwindigkeit ist v_{\text{max}} = 32.34.

Bei allen Aufgabenteilen sind nur die Zahlen auf mindestens zwei Nachkommastellen genau anzugeben, keine Einheiten!

Bestimmen Sie den Parameter A =

Welche Strecke (in m) legt das Gefährt während der gesamten 14 Sekunden zurück? s(14) =

Wie hoch ist die durchschnittliche Geschwindigkeit (in m/s)? \overline{v}=

Welchen Anteil (in Prozent) der gesamten Strecke legt das Gefährt zwischen t = 5.7 und t= 7.7 zurück?

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 7 maximal. Um nun A zu bestimmen muss daher gelten

\begin{aligned} 32.34 & = A \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = A \cdot 7 \cdot (14 - 7) \end{aligned}

Löst man diesen Ausdruck nach A auf, so ergibt sich: A = 0.66.

Da die nächsten Aufgabenteile alle eine Integration von v benötigen, bestimmen wir s(T). Dies entspricht der zum Zeitpunkt T zurückgelegten Strecke:

\begin{aligned} s(T) & = \int_{0}^T v(t)\,\mathrm{d}t \\ & = \int_{0}^T 0.66 \cdot t \cdot (14 - t)\,\mathrm{d}t\\ & = \int_{0}^T 9.24 \cdot t - 0.66 \cdot t^2\,\mathrm{d}t \\ & = 4.62 \cdot T^2 - 0.22 \cdot T^3 \end{aligned} Die untere Grenze ist identisch 0, daher wurde diese im letzten Schritt gleich weggelassen. Damit kann man nun die restlichen Aufgaben lösen:

\begin{aligned} s(t_{\text{max}}) = s(14) & = 4.62 \cdot 14^2 - 0.22 \cdot 14^3 \\ & = 301.84 \end{aligned} Für die Durchschnittsgeschwindigkeit teilt man die zurückgelegte Strecke durch die Gesamtzeit der Fahrt. Es ergibt sich:

\overline{v} = \frac{s(14)}{14} = 21.56 Der Anteil, bestimmt man indem man die im Zeitintervall 5.7 bis 7.7 zurückgelegte Strecke durch die gesamte Strecke teilt. Es ergibt sich:

\begin{aligned} p = \frac{\int_{5.7}^{7.7} v(t)\,\mathrm{d}t}{\int_{0}^{14} v(t)\,\mathrm{d}t} & = \frac{s(7.7) - s(5.7)}{s(14) - s(0)} \\ & = \frac{173.48254 - 109.36134}{301.84 - 0} \\ & = 0.2124 \end{aligned}

Dies sind 21.24 Prozent.

A = 0.66
s(14) = 301.84
\overline{v} = 21.56
p = 21.24\%

Im folgenden Diagramm ist das Geschwindigkeits-Zeit-Diagramm eines Gefährts abgebildet. Der Graph der Funktion ist eine nach unten offene Parabel der Form

v(t) = A \cdot t \cdot (t_{\text{max}} -t) \qquad \text{mit} \qquad t_{\text{max}} = 14.

Die maximal erreichte Geschwindigkeit ist v_{\text{max}} = 32.34.

Bei allen Aufgabenteilen sind nur die Zahlen auf mindestens zwei Nachkommastellen genau anzugeben, keine Einheiten!

Bestimmen Sie den Parameter A =

Welche Strecke (in m) legt das Gefährt während der gesamten 14 Sekunden zurück? s(14) =

Wie hoch ist die durchschnittliche Geschwindigkeit (in m/s)? \overline{v}=

Welchen Anteil (in Prozent) der gesamten Strecke legt das Gefährt zwischen t = 4.5 und t= 7.3 zurück?

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 7 maximal. Um nun A zu bestimmen muss daher gelten

\begin{aligned} 32.34 & = A \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = A \cdot 7 \cdot (14 - 7) \end{aligned}

Löst man diesen Ausdruck nach A auf, so ergibt sich: A = 0.66.

Da die nächsten Aufgabenteile alle eine Integration von v benötigen, bestimmen wir s(T). Dies entspricht der zum Zeitpunkt T zurückgelegten Strecke:

\overline{v} = \frac{s(14)}{14} = 21.56 Der Anteil, bestimmt man indem man die im Zeitintervall 4.5 bis 7.3 zurückgelegte Strecke durch die gesamte Strecke teilt. Es ergibt sich:

\begin{aligned} p = \frac{\int_{4.5}^{7.3} v(t)\,\mathrm{d}t}{\int_{0}^{14} v(t)\,\mathrm{d}t} & = \frac{s(7.3) - s(4.5)}{s(14) - s(0)} \\ & = \frac{160.61606 - 73.5075}{301.84 - 0} \\ & = 0.2886 \end{aligned}

Dies sind 28.86 Prozent.

A = 0.66
s(14) = 301.84
\overline{v} = 21.56
p = 28.86\%

Im folgenden Diagramm ist das Geschwindigkeits-Zeit-Diagramm eines Gefährts abgebildet. Der Graph der Funktion ist eine nach unten offene Parabel der Form

v(t) = A \cdot t \cdot (t_{\text{max}} -t) \qquad \text{mit} \qquad t_{\text{max}} = 6.

Die maximal erreichte Geschwindigkeit ist v_{\text{max}} = 18.36.

Bei allen Aufgabenteilen sind nur die Zahlen auf mindestens zwei Nachkommastellen genau anzugeben, keine Einheiten!

Bestimmen Sie den Parameter A =

Welche Strecke (in m) legt das Gefährt während der gesamten 6 Sekunden zurück? s(6) =

Wie hoch ist die durchschnittliche Geschwindigkeit (in m/s)? \overline{v}=

Welchen Anteil (in Prozent) der gesamten Strecke legt das Gefährt zwischen t = 0.8 und t= 4.5 zurück?

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 3 maximal. Um nun A zu bestimmen muss daher gelten

\begin{aligned} 18.36 & = A \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = A \cdot 3 \cdot (6 - 3) \end{aligned}

Löst man diesen Ausdruck nach A auf, so ergibt sich: A = 2.04.

Da die nächsten Aufgabenteile alle eine Integration von v benötigen, bestimmen wir s(T). Dies entspricht der zum Zeitpunkt T zurückgelegten Strecke:

\begin{aligned} s(T) & = \int_{0}^T v(t)\,\mathrm{d}t \\ & = \int_{0}^T 2.04 \cdot t \cdot (6 - t)\,\mathrm{d}t\\ & = \int_{0}^T 12.24 \cdot t - 2.04 \cdot t^2\,\mathrm{d}t \\ & = 6.12 \cdot T^2 - 0.68 \cdot T^3 \end{aligned} Die untere Grenze ist identisch 0, daher wurde diese im letzten Schritt gleich weggelassen. Damit kann man nun die restlichen Aufgaben lösen:

\begin{aligned} s(t_{\text{max}}) = s(6) & = 6.12 \cdot 6^2 - 0.68 \cdot 6^3 \\ & = 73.44 \end{aligned} Für die Durchschnittsgeschwindigkeit teilt man die zurückgelegte Strecke durch die Gesamtzeit der Fahrt. Es ergibt sich:

\overline{v} = \frac{s(6)}{6} = 12.24 Der Anteil, bestimmt man indem man die im Zeitintervall 0.8 bis 4.5 zurückgelegte Strecke durch die gesamte Strecke teilt. Es ergibt sich:

\begin{aligned} p = \frac{\int_{0.8}^{4.5} v(t)\,\mathrm{d}t}{\int_{0}^{6} v(t)\,\mathrm{d}t} & = \frac{s(4.5) - s(0.8)}{s(6) - s(0)} \\ & = \frac{61.965 - 3.56864}{73.44 - 0} \\ & = 0.7952 \end{aligned}

Dies sind 79.52 Prozent.

A = 2.04
s(6) = 73.44
\overline{v} = 12.24
p = 79.52\%

Im folgenden Diagramm ist das Geschwindigkeits-Zeit-Diagramm eines Gefährts abgebildet. Der Graph der Funktion ist eine nach unten offene Parabel der Form

v(t) = A \cdot t \cdot (t_{\text{max}} -t) \qquad \text{mit} \qquad t_{\text{max}} = 4.

Die maximal erreichte Geschwindigkeit ist v_{\text{max}} = 12.72.

Bei allen Aufgabenteilen sind nur die Zahlen auf mindestens zwei Nachkommastellen genau anzugeben, keine Einheiten!

Bestimmen Sie den Parameter A =

Welche Strecke (in m) legt das Gefährt während der gesamten 4 Sekunden zurück? s(4) =

Wie hoch ist die durchschnittliche Geschwindigkeit (in m/s)? \overline{v}=

Welchen Anteil (in Prozent) der gesamten Strecke legt das Gefährt zwischen t = 1.1 und t= 2.2 zurück?

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 2 maximal. Um nun A zu bestimmen muss daher gelten

\begin{aligned} 12.72 & = A \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = A \cdot 2 \cdot (4 - 2) \end{aligned}

Löst man diesen Ausdruck nach A auf, so ergibt sich: A = 3.18.

Da die nächsten Aufgabenteile alle eine Integration von v benötigen, bestimmen wir s(T). Dies entspricht der zum Zeitpunkt T zurückgelegten Strecke:

\begin{aligned} s(T) & = \int_{0}^T v(t)\,\mathrm{d}t \\ & = \int_{0}^T 3.18 \cdot t \cdot (4 - t)\,\mathrm{d}t\\ & = \int_{0}^T 12.72 \cdot t - 3.18 \cdot t^2\,\mathrm{d}t \\ & = 6.36 \cdot T^2 - 1.06 \cdot T^3 \end{aligned} Die untere Grenze ist identisch 0, daher wurde diese im letzten Schritt gleich weggelassen. Damit kann man nun die restlichen Aufgaben lösen:

\begin{aligned} s(t_{\text{max}}) = s(4) & = 6.36 \cdot 4^2 - 1.06 \cdot 4^3 \\ & = 33.92 \end{aligned} Für die Durchschnittsgeschwindigkeit teilt man die zurückgelegte Strecke durch die Gesamtzeit der Fahrt. Es ergibt sich:

\overline{v} = \frac{s(4)}{4} = 8.48 Der Anteil, bestimmt man indem man die im Zeitintervall 1.1 bis 2.2 zurückgelegte Strecke durch die gesamte Strecke teilt. Es ergibt sich:

\begin{aligned} p = \frac{\int_{1.1}^{2.2} v(t)\,\mathrm{d}t}{\int_{0}^{4} v(t)\,\mathrm{d}t} & = \frac{s(2.2) - s(1.1)}{s(4) - s(0)} \\ & = \frac{19.49552 - 6.28474}{33.92 - 0} \\ & = 0.3895 \end{aligned}

Dies sind 38.95 Prozent.

A = 3.18
s(4) = 33.92
\overline{v} = 8.48
p = 38.95\%

Im folgenden Diagramm ist das Geschwindigkeits-Zeit-Diagramm eines Gefährts abgebildet. Der Graph der Funktion ist eine nach unten offene Parabel der Form

v(t) = A \cdot t \cdot (t_{\text{max}} -t) \qquad \text{mit} \qquad t_{\text{max}} = 4.

Die maximal erreichte Geschwindigkeit ist v_{\text{max}} = 11.52.

Bei allen Aufgabenteilen sind nur die Zahlen auf mindestens zwei Nachkommastellen genau anzugeben, keine Einheiten!

Bestimmen Sie den Parameter A =

Welche Strecke (in m) legt das Gefährt während der gesamten 4 Sekunden zurück? s(4) =

Wie hoch ist die durchschnittliche Geschwindigkeit (in m/s)? \overline{v}=

Welchen Anteil (in Prozent) der gesamten Strecke legt das Gefährt zwischen t = 1.4 und t= 2.5 zurück?

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 2 maximal. Um nun A zu bestimmen muss daher gelten

\begin{aligned} 11.52 & = A \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = A \cdot 2 \cdot (4 - 2) \end{aligned}

Löst man diesen Ausdruck nach A auf, so ergibt sich: A = 2.88.

Da die nächsten Aufgabenteile alle eine Integration von v benötigen, bestimmen wir s(T). Dies entspricht der zum Zeitpunkt T zurückgelegten Strecke:

\begin{aligned} s(T) & = \int_{0}^T v(t)\,\mathrm{d}t \\ & = \int_{0}^T 2.88 \cdot t \cdot (4 - t)\,\mathrm{d}t\\ & = \int_{0}^T 11.52 \cdot t - 2.88 \cdot t^2\,\mathrm{d}t \\ & = 5.76 \cdot T^2 - 0.96 \cdot T^3 \end{aligned} Die untere Grenze ist identisch 0, daher wurde diese im letzten Schritt gleich weggelassen. Damit kann man nun die restlichen Aufgaben lösen:

\begin{aligned} s(t_{\text{max}}) = s(4) & = 5.76 \cdot 4^2 - 0.96 \cdot 4^3 \\ & = 30.72 \end{aligned} Für die Durchschnittsgeschwindigkeit teilt man die zurückgelegte Strecke durch die Gesamtzeit der Fahrt. Es ergibt sich:

\overline{v} = \frac{s(4)}{4} = 7.68 Der Anteil, bestimmt man indem man die im Zeitintervall 1.4 bis 2.5 zurückgelegte Strecke durch die gesamte Strecke teilt. Es ergibt sich:

\begin{aligned} p = \frac{\int_{1.4}^{2.5} v(t)\,\mathrm{d}t}{\int_{0}^{4} v(t)\,\mathrm{d}t} & = \frac{s(2.5) - s(1.4)}{s(4) - s(0)} \\ & = \frac{21 - 8.65536}{30.72 - 0} \\ & = 0.4018 \end{aligned}

Dies sind 40.18 Prozent.

A = 2.88
s(4) = 30.72
\overline{v} = 7.68
p = 40.18\%

Im folgenden Diagramm ist das Geschwindigkeits-Zeit-Diagramm eines Gefährts abgebildet. Der Graph der Funktion ist eine nach unten offene Parabel der Form

v(t) = A \cdot t \cdot (t_{\text{max}} -t) \qquad \text{mit} \qquad t_{\text{max}} = 6.

Die maximal erreichte Geschwindigkeit ist v_{\text{max}} = 48.06.

Bei allen Aufgabenteilen sind nur die Zahlen auf mindestens zwei Nachkommastellen genau anzugeben, keine Einheiten!

Bestimmen Sie den Parameter A =

Welche Strecke (in m) legt das Gefährt während der gesamten 6 Sekunden zurück? s(6) =

Wie hoch ist die durchschnittliche Geschwindigkeit (in m/s)? \overline{v}=

Welchen Anteil (in Prozent) der gesamten Strecke legt das Gefährt zwischen t = 2.9 und t= 5.1 zurück?

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 3 maximal. Um nun A zu bestimmen muss daher gelten

\begin{aligned} 48.06 & = A \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = A \cdot 3 \cdot (6 - 3) \end{aligned}

Löst man diesen Ausdruck nach A auf, so ergibt sich: A = 5.34.

Da die nächsten Aufgabenteile alle eine Integration von v benötigen, bestimmen wir s(T). Dies entspricht der zum Zeitpunkt T zurückgelegten Strecke:

\begin{aligned} s(T) & = \int_{0}^T v(t)\,\mathrm{d}t \\ & = \int_{0}^T 5.34 \cdot t \cdot (6 - t)\,\mathrm{d}t\\ & = \int_{0}^T 32.04 \cdot t - 5.34 \cdot t^2\,\mathrm{d}t \\ & = 16.02 \cdot T^2 - 1.78 \cdot T^3 \end{aligned} Die untere Grenze ist identisch 0, daher wurde diese im letzten Schritt gleich weggelassen. Damit kann man nun die restlichen Aufgaben lösen:

\begin{aligned} s(t_{\text{max}}) = s(6) & = 16.02 \cdot 6^2 - 1.78 \cdot 6^3 \\ & = 192.24 \end{aligned} Für die Durchschnittsgeschwindigkeit teilt man die zurückgelegte Strecke durch die Gesamtzeit der Fahrt. Es ergibt sich:

\overline{v} = \frac{s(6)}{6} = 32.04 Der Anteil, bestimmt man indem man die im Zeitintervall 2.9 bis 5.1 zurückgelegte Strecke durch die gesamte Strecke teilt. Es ergibt sich:

\begin{aligned} p = \frac{\int_{2.9}^{5.1} v(t)\,\mathrm{d}t}{\int_{0}^{6} v(t)\,\mathrm{d}t} & = \frac{s(5.1) - s(2.9)}{s(6) - s(0)} \\ & = \frac{180.56142 - 91.31578}{192.24 - 0} \\ & = 0.4642 \end{aligned}

Dies sind 46.42 Prozent.

A = 5.34
s(6) = 192.24
\overline{v} = 32.04
p = 46.42\%

Im folgenden Diagramm ist das Geschwindigkeits-Zeit-Diagramm eines Gefährts abgebildet. Der Graph der Funktion ist eine nach unten offene Parabel der Form

v(t) = A \cdot t \cdot (t_{\text{max}} -t) \qquad \text{mit} \qquad t_{\text{max}} = 10.

Die maximal erreichte Geschwindigkeit ist v_{\text{max}} = 37.5.

Bei allen Aufgabenteilen sind nur die Zahlen auf mindestens zwei Nachkommastellen genau anzugeben, keine Einheiten!

Bestimmen Sie den Parameter A =

Welche Strecke (in m) legt das Gefährt während der gesamten 10 Sekunden zurück? s(10) =

Wie hoch ist die durchschnittliche Geschwindigkeit (in m/s)? \overline{v}=

Welchen Anteil (in Prozent) der gesamten Strecke legt das Gefährt zwischen t = 3.3 und t= 8.9 zurück?

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 5 maximal. Um nun A zu bestimmen muss daher gelten

\begin{aligned} 37.5 & = A \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = A \cdot 5 \cdot (10 - 5) \end{aligned}

Löst man diesen Ausdruck nach A auf, so ergibt sich: A = 1.5.

Da die nächsten Aufgabenteile alle eine Integration von v benötigen, bestimmen wir s(T). Dies entspricht der zum Zeitpunkt T zurückgelegten Strecke:

\begin{aligned} s(T) & = \int_{0}^T v(t)\,\mathrm{d}t \\ & = \int_{0}^T 1.5 \cdot t \cdot (10 - t)\,\mathrm{d}t\\ & = \int_{0}^T 15 \cdot t - 1.5 \cdot t^2\,\mathrm{d}t \\ & = 7.5 \cdot T^2 - 0.5 \cdot T^3 \end{aligned} Die untere Grenze ist identisch 0, daher wurde diese im letzten Schritt gleich weggelassen. Damit kann man nun die restlichen Aufgaben lösen:

\begin{aligned} s(t_{\text{max}}) = s(10) & = 7.5 \cdot 10^2 - 0.5 \cdot 10^3 \\ & = 250 \end{aligned} Für die Durchschnittsgeschwindigkeit teilt man die zurückgelegte Strecke durch die Gesamtzeit der Fahrt. Es ergibt sich:

\overline{v} = \frac{s(10)}{10} = 25 Der Anteil, bestimmt man indem man die im Zeitintervall 3.3 bis 8.9 zurückgelegte Strecke durch die gesamte Strecke teilt. Es ergibt sich:

\begin{aligned} p = \frac{\int_{3.3}^{8.9} v(t)\,\mathrm{d}t}{\int_{0}^{10} v(t)\,\mathrm{d}t} & = \frac{s(8.9) - s(3.3)}{s(10) - s(0)} \\ & = \frac{241.5905 - 63.7065}{250 - 0} \\ & = 0.7115 \end{aligned}

Dies sind 71.15 Prozent.

A = 1.5
s(10) = 250
\overline{v} = 25
p = 71.15\%

Im folgenden Diagramm ist das Geschwindigkeits-Zeit-Diagramm eines Gefährts abgebildet. Der Graph der Funktion ist eine nach unten offene Parabel der Form

v(t) = A \cdot t \cdot (t_{\text{max}} -t) \qquad \text{mit} \qquad t_{\text{max}} = 14.

Die maximal erreichte Geschwindigkeit ist v_{\text{max}} = 47.04.

Bei allen Aufgabenteilen sind nur die Zahlen auf mindestens zwei Nachkommastellen genau anzugeben, keine Einheiten!

Bestimmen Sie den Parameter A =

Welche Strecke (in m) legt das Gefährt während der gesamten 14 Sekunden zurück? s(14) =

Wie hoch ist die durchschnittliche Geschwindigkeit (in m/s)? \overline{v}=

Welchen Anteil (in Prozent) der gesamten Strecke legt das Gefährt zwischen t = 6 und t= 10.1 zurück?

Die Funktion v(t) wird bei t = \frac{t_{\text{max}}}{2} = 7 maximal. Um nun A zu bestimmen muss daher gelten

\begin{aligned} 47.04 & = A \cdot \frac{t_{\text{max}}}{2} \cdot \left(t_{\text{max}} - \frac{t_{\text{max}}}{2}\right) \\ & = A \cdot 7 \cdot (14 - 7) \end{aligned}

Löst man diesen Ausdruck nach A auf, so ergibt sich: A = 0.96.

Da die nächsten Aufgabenteile alle eine Integration von v benötigen, bestimmen wir s(T). Dies entspricht der zum Zeitpunkt T zurückgelegten Strecke:

\begin{aligned} s(T) & = \int_{0}^T v(t)\,\mathrm{d}t \\ & = \int_{0}^T 0.96 \cdot t \cdot (14 - t)\,\mathrm{d}t\\ & = \int_{0}^T 13.44 \cdot t - 0.96 \cdot t^2\,\mathrm{d}t \\ & = 6.72 \cdot T^2 - 0.32 \cdot T^3 \end{aligned} Die untere Grenze ist identisch 0, daher wurde diese im letzten Schritt gleich weggelassen. Damit kann man nun die restlichen Aufgaben lösen:

\begin{aligned} s(t_{\text{max}}) = s(14) & = 6.72 \cdot 14^2 - 0.32 \cdot 14^3 \\ & = 439.04 \end{aligned} Für die Durchschnittsgeschwindigkeit teilt man die zurückgelegte Strecke durch die Gesamtzeit der Fahrt. Es ergibt sich:

\overline{v} = \frac{s(14)}{14} = 31.36 Der Anteil, bestimmt man indem man die im Zeitintervall 6 bis 10.1 zurückgelegte Strecke durch die gesamte Strecke teilt. Es ergibt sich:

\begin{aligned} p = \frac{\int_{6}^{10.1} v(t)\,\mathrm{d}t}{\int_{0}^{14} v(t)\,\mathrm{d}t} & = \frac{s(10.1) - s(6)}{s(14) - s(0)} \\ & = \frac{355.81088 - 172.8}{439.04 - 0} \\ & = 0.4168 \end{aligned}

Dies sind 41.68 Prozent.

A = 0.96
s(14) = 439.04
\overline{v} = 31.36
p = 41.68\%

Gegeben ist die Funktion f: \mathbb{R} \to \mathbb{R} mit

f(x) = x \cdot (x-a)\cdot (x-b), \quad \text{mit } 0 < a < b. Ferner definieren wir die Funktion g(x) = |f(x)|.

Der Graph zeigt die Funktion g für die Werte a = und b = .

Bestimmen Sie die eingefärbte Fläche A = \int_0^{3.9} g(x)\,\mathrm{d}x =

Offenbar kann man a = 2.1 aus der Grafik ablesen. Betrachten wir die Funktion f und muiltiplizieren diese aus um sie dann später integrieren zu können:

\begin{aligned} f(x) & = x \cdot (x-a)\cdot (x-3.9) \\ & = x^3 -(a+3.9) x^2 + 3.9ax \\ & = x^3 - 6 x^2 + 8.19 x \end{aligned} Damit ergibt sich die Stammfunktion

\begin{aligned} F(x) & = \frac{1}{4}x^4 - \frac{a+3.9}{3} x^3 + 1.95ax^2 + C \\ & = 0.25x^4 - 2x^3 + 4.095 x^2 + C \end{aligned}

Um das Intergal \int\limits_{0}^{3.9} g(x)\,\mathrm{d} x zerlegt man das Integral in zwei Teile und nutzt die Tatsache, dass f(x) > 0 für x \in (0, 2.1) und f(x) < 0 für x \in (2.1, 3.9). Damit ergibt sich:

\begin{aligned} \int\limits_{0}^{3.9} g(x)\,\mathrm{d} x & = \int\limits_{0}^{2.1} f(x)\,\mathrm{d} x + \int\limits_{2.1}^{3.9} (-f(x))\,\mathrm{d} x \\ & = \int\limits_{0}^{2.1} f(x)\,\mathrm{d} x - \int\limits_{2.1}^{3.9} f(x)\,\mathrm{d} x \\ & = F(2.1) - F(0) - F(3.9) + F(2.1) \\ & = 2F(2.1) - F(0) -F(3.9) \\ & \approx 21.7829 \end{aligned}

a = 2.1
b = 3.9
A = 21.7829

Gegeben ist die Funktion f: \mathbb{R} \to \mathbb{R} mit

f(x) = x \cdot (x-a)\cdot (x-b), \quad \text{mit } 0 < a < b. Ferner definieren wir die Funktion g(x) = |f(x)|.

Der Graph zeigt die Funktion g für die Werte a = und b = .

Bestimmen Sie die eingefärbte Fläche A = \int_0^{3.9} g(x)\,\mathrm{d}x =

Offenbar kann man a = 3.6 aus der Grafik ablesen. Betrachten wir die Funktion f und muiltiplizieren diese aus um sie dann später integrieren zu können:

\begin{aligned} f(x) & = x \cdot (x-a)\cdot (x-3.9) \\ & = x^3 -(a+3.9) x^2 + 3.9ax \\ & = x^3 - 7.5 x^2 + 14.04 x \end{aligned} Damit ergibt sich die Stammfunktion

\begin{aligned} F(x) & = \frac{1}{4}x^4 - \frac{a+3.9}{3} x^3 + 1.95ax^2 + C \\ & = 0.25x^4 - 2.5x^3 + 7.02 x^2 + C \end{aligned}

Um das Intergal \int\limits_{0}^{3.9} g(x)\,\mathrm{d} x zerlegt man das Integral in zwei Teile und nutzt die Tatsache, dass f(x) > 0 für x \in (0, 3.6) und f(x) < 0 für x \in (3.6, 3.9). Damit ergibt sich:

\begin{aligned} \int\limits_{0}^{3.9} g(x)\,\mathrm{d} x & = \int\limits_{0}^{3.6} f(x)\,\mathrm{d} x + \int\limits_{3.6}^{3.9} (-f(x))\,\mathrm{d} x \\ & = \int\limits_{0}^{3.6} f(x)\,\mathrm{d} x - \int\limits_{3.6}^{3.9} f(x)\,\mathrm{d} x \\ & = F(3.6) - F(0) - F(3.9) + F(3.6) \\ & = 2F(3.6) - F(0) -F(3.9) \\ & \approx 33.0352 \end{aligned}

a = 3.6
b = 3.9
A = 33.0352

Gegeben ist die Funktion f: \mathbb{R} \to \mathbb{R} mit

f(x) = x \cdot (x-a)\cdot (x-b), \quad \text{mit } 0 < a < b. Ferner definieren wir die Funktion g(x) = |f(x)|.

Der Graph zeigt die Funktion g für die Werte a = und b = .

Bestimmen Sie die eingefärbte Fläche A = \int_0^{6.3} g(x)\,\mathrm{d}x =

Offenbar kann man a = 1.8 aus der Grafik ablesen. Betrachten wir die Funktion f und muiltiplizieren diese aus um sie dann später integrieren zu können:

\begin{aligned} f(x) & = x \cdot (x-a)\cdot (x-6.3) \\ & = x^3 -(a+6.3) x^2 + 6.3ax \\ & = x^3 - 8.1 x^2 + 11.34 x \end{aligned} Damit ergibt sich die Stammfunktion

\begin{aligned} F(x) & = \frac{1}{4}x^4 - \frac{a+6.3}{3} x^3 + 3.15ax^2 + C \\ & = 0.25x^4 - 2.7x^3 + 5.67 x^2 + C \end{aligned}

Um das Intergal \int\limits_{0}^{6.3} g(x)\,\mathrm{d} x zerlegt man das Integral in zwei Teile und nutzt die Tatsache, dass f(x) > 0 für x \in (0, 1.8) und f(x) < 0 für x \in (1.8, 6.3). Damit ergibt sich:

\begin{aligned} \int\limits_{0}^{6.3} g(x)\,\mathrm{d} x & = \int\limits_{0}^{1.8} f(x)\,\mathrm{d} x + \int\limits_{1.8}^{6.3} (-f(x))\,\mathrm{d} x \\ & = \int\limits_{0}^{1.8} f(x)\,\mathrm{d} x - \int\limits_{1.8}^{6.3} f(x)\,\mathrm{d} x \\ & = F(1.8) - F(0) - F(6.3) + F(1.8) \\ & = 2F(1.8) - F(0) -F(6.3) \\ & \approx 51.8866 \end{aligned}

a = 1.8
b = 6.3
A = 51.8866

Gegeben ist die Funktion f: \mathbb{R} \to \mathbb{R} mit

f(x) = x \cdot (x-a)\cdot (x-b), \quad \text{mit } 0 < a < b. Ferner definieren wir die Funktion g(x) = |f(x)|.

Der Graph zeigt die Funktion g für die Werte a = und b = .

Bestimmen Sie die eingefärbte Fläche A = \int_0^{5.1} g(x)\,\mathrm{d}x =

Offenbar kann man a = 2.1 aus der Grafik ablesen. Betrachten wir die Funktion f und muiltiplizieren diese aus um sie dann später integrieren zu können:

\begin{aligned} f(x) & = x \cdot (x-a)\cdot (x-5.1) \\ & = x^3 -(a+5.1) x^2 + 5.1ax \\ & = x^3 - 7.2 x^2 + 10.71 x \end{aligned} Damit ergibt sich die Stammfunktion

\begin{aligned} F(x) & = \frac{1}{4}x^4 - \frac{a+5.1}{3} x^3 + 2.55ax^2 + C \\ & = 0.25x^4 - 2.4x^3 + 5.355 x^2 + C \end{aligned}

Um das Intergal \int\limits_{0}^{5.1} g(x)\,\mathrm{d} x zerlegt man das Integral in zwei Teile und nutzt die Tatsache, dass f(x) > 0 für x \in (0, 2.1) und f(x) < 0 für x \in (2.1, 5.1). Damit ergibt sich:

\begin{aligned} \int\limits_{0}^{5.1} g(x)\,\mathrm{d} x & = \int\limits_{0}^{2.1} f(x)\,\mathrm{d} x + \int\limits_{2.1}^{5.1} (-f(x))\,\mathrm{d} x \\ & = \int\limits_{0}^{2.1} f(x)\,\mathrm{d} x - \int\limits_{2.1}^{5.1} f(x)\,\mathrm{d} x \\ & = F(2.1) - F(0) - F(5.1) + F(2.1) \\ & = 2F(2.1) - F(0) -F(5.1) \\ & \approx 40.4453 \end{aligned}

a = 2.1
b = 5.1
A = 40.4453

Gegeben ist die Funktion f: \mathbb{R} \to \mathbb{R} mit

f(x) = x \cdot (x-a)\cdot (x-b), \quad \text{mit } 0 < a < b. Ferner definieren wir die Funktion g(x) = |f(x)|.

Der Graph zeigt die Funktion g für die Werte a = und b = .

Bestimmen Sie die eingefärbte Fläche A = \int_0^{5.7} g(x)\,\mathrm{d}x =

Offenbar kann man a = 2.4 aus der Grafik ablesen. Betrachten wir die Funktion f und muiltiplizieren diese aus um sie dann später integrieren zu können:

\begin{aligned} f(x) & = x \cdot (x-a)\cdot (x-5.7) \\ & = x^3 -(a+5.7) x^2 + 5.7ax \\ & = x^3 - 8.1 x^2 + 13.68 x \end{aligned} Damit ergibt sich die Stammfunktion

\begin{aligned} F(x) & = \frac{1}{4}x^4 - \frac{a+5.7}{3} x^3 + 2.85ax^2 + C \\ & = 0.25x^4 - 2.7x^3 + 6.84 x^2 + C \end{aligned}

Um das Intergal \int\limits_{0}^{5.7} g(x)\,\mathrm{d} x zerlegt man das Integral in zwei Teile und nutzt die Tatsache, dass f(x) > 0 für x \in (0, 2.4) und f(x) < 0 für x \in (2.4, 5.7). Damit ergibt sich:

\begin{aligned} \int\limits_{0}^{5.7} g(x)\,\mathrm{d} x & = \int\limits_{0}^{2.4} f(x)\,\mathrm{d} x + \int\limits_{2.4}^{5.7} (-f(x))\,\mathrm{d} x \\ & = \int\limits_{0}^{2.4} f(x)\,\mathrm{d} x - \int\limits_{2.4}^{5.7} f(x)\,\mathrm{d} x \\ & = F(2.4) - F(0) - F(5.7) + F(2.4) \\ & = 2F(2.4) - F(0) -F(5.7) \\ & \approx 42.8308 \end{aligned}

a = 2.4
b = 5.7
A = 42.8308

Gegeben ist die Funktion f: \mathbb{R} \to \mathbb{R} mit

f(x) = x \cdot (x-a)\cdot (x-b), \quad \text{mit } 0 < a < b. Ferner definieren wir die Funktion g(x) = |f(x)|.

Der Graph zeigt die Funktion g für die Werte a = und b = .

Bestimmen Sie die eingefärbte Fläche A = \int_0^{3.9} g(x)\,\mathrm{d}x =

Offenbar kann man a = 2.7 aus der Grafik ablesen. Betrachten wir die Funktion f und muiltiplizieren diese aus um sie dann später integrieren zu können:

\begin{aligned} f(x) & = x \cdot (x-a)\cdot (x-3.9) \\ & = x^3 -(a+3.9) x^2 + 3.9ax \\ & = x^3 - 6.6 x^2 + 10.53 x \end{aligned} Damit ergibt sich die Stammfunktion

\begin{aligned} F(x) & = \frac{1}{4}x^4 - \frac{a+3.9}{3} x^3 + 1.95ax^2 + C \\ & = 0.25x^4 - 2.2x^3 + 5.265 x^2 + C \end{aligned}

Um das Intergal \int\limits_{0}^{3.9} g(x)\,\mathrm{d} x zerlegt man das Integral in zwei Teile und nutzt die Tatsache, dass f(x) > 0 für x \in (0, 2.7) und f(x) < 0 für x \in (2.7, 3.9). Damit ergibt sich:

\begin{aligned} \int\limits_{0}^{3.9} g(x)\,\mathrm{d} x & = \int\limits_{0}^{2.7} f(x)\,\mathrm{d} x + \int\limits_{2.7}^{3.9} (-f(x))\,\mathrm{d} x \\ & = \int\limits_{0}^{2.7} f(x)\,\mathrm{d} x - \int\limits_{2.7}^{3.9} f(x)\,\mathrm{d} x \\ & = F(2.7) - F(0) - F(3.9) + F(2.7) \\ & = 2F(2.7) - F(0) -F(3.9) \\ & \approx 21.4967 \end{aligned}

a = 2.7
b = 3.9
A = 21.4967

Gegeben ist die Funktion f: \mathbb{R} \to \mathbb{R} mit

f(x) = x \cdot (x-a)\cdot (x-b), \quad \text{mit } 0 < a < b. Ferner definieren wir die Funktion g(x) = |f(x)|.

Der Graph zeigt die Funktion g für die Werte a = und b = .

Bestimmen Sie die eingefärbte Fläche A = \int_0^{5.1} g(x)\,\mathrm{d}x =

Offenbar kann man a = 4.2 aus der Grafik ablesen. Betrachten wir die Funktion f und muiltiplizieren diese aus um sie dann später integrieren zu können:

\begin{aligned} f(x) & = x \cdot (x-a)\cdot (x-5.1) \\ & = x^3 -(a+5.1) x^2 + 5.1ax \\ & = x^3 - 9.3 x^2 + 21.42 x \end{aligned} Damit ergibt sich die Stammfunktion

\begin{aligned} F(x) & = \frac{1}{4}x^4 - \frac{a+5.1}{3} x^3 + 2.55ax^2 + C \\ & = 0.25x^4 - 3.1x^3 + 10.71 x^2 + C \end{aligned}

Um das Intergal \int\limits_{0}^{5.1} g(x)\,\mathrm{d} x zerlegt man das Integral in zwei Teile und nutzt die Tatsache, dass f(x) > 0 für x \in (0, 4.2) und f(x) < 0 für x \in (4.2, 5.1). Damit ergibt sich:

\begin{aligned} \int\limits_{0}^{5.1} g(x)\,\mathrm{d} x & = \int\limits_{0}^{4.2} f(x)\,\mathrm{d} x + \int\limits_{4.2}^{5.1} (-f(x))\,\mathrm{d} x \\ & = \int\limits_{0}^{4.2} f(x)\,\mathrm{d} x - \int\limits_{4.2}^{5.1} f(x)\,\mathrm{d} x \\ & = F(4.2) - F(0) - F(5.1) + F(4.2) \\ & = 2F(4.2) - F(0) -F(5.1) \\ & \approx 50.4718 \end{aligned}

a = 4.2
b = 5.1
A = 50.4718

Gegeben ist die Funktion f: \mathbb{R} \to \mathbb{R} mit

f(x) = x \cdot (x-a)\cdot (x-b), \quad \text{mit } 0 < a < b. Ferner definieren wir die Funktion g(x) = |f(x)|.

Der Graph zeigt die Funktion g für die Werte a = und b = .

Bestimmen Sie die eingefärbte Fläche A = \int_0^{4.5} g(x)\,\mathrm{d}x =

Offenbar kann man a = 3 aus der Grafik ablesen. Betrachten wir die Funktion f und muiltiplizieren diese aus um sie dann später integrieren zu können:

\begin{aligned} f(x) & = x \cdot (x-a)\cdot (x-4.5) \\ & = x^3 -(a+4.5) x^2 + 4.5ax \\ & = x^3 - 7.5 x^2 + 13.5 x \end{aligned} Damit ergibt sich die Stammfunktion

\begin{aligned} F(x) & = \frac{1}{4}x^4 - \frac{a+4.5}{3} x^3 + 2.25ax^2 + C \\ & = 0.25x^4 - 2.5x^3 + 6.75 x^2 + C \end{aligned}

Um das Intergal \int\limits_{0}^{4.5} g(x)\,\mathrm{d} x zerlegt man das Integral in zwei Teile und nutzt die Tatsache, dass f(x) > 0 für x \in (0, 3) und f(x) < 0 für x \in (3, 4.5). Damit ergibt sich:

\begin{aligned} \int\limits_{0}^{4.5} g(x)\,\mathrm{d} x & = \int\limits_{0}^{3} f(x)\,\mathrm{d} x + \int\limits_{3}^{4.5} (-f(x))\,\mathrm{d} x \\ & = \int\limits_{0}^{3} f(x)\,\mathrm{d} x - \int\limits_{3}^{4.5} f(x)\,\mathrm{d} x \\ & = F(3) - F(0) - F(4.5) + F(3) \\ & = 2F(3) - F(0) -F(4.5) \\ & \approx 29.1094 \end{aligned}

a = 3
b = 4.5
A = 29.1094

Gegeben ist die Funktion f: \mathbb{R} \to \mathbb{R} mit

f(x) = x \cdot (x-a)\cdot (x-b), \quad \text{mit } 0 < a < b. Ferner definieren wir die Funktion g(x) = |f(x)|.

Der Graph zeigt die Funktion g für die Werte a = und b = .

Bestimmen Sie die eingefärbte Fläche A = \int_0^{6.9} g(x)\,\mathrm{d}x =

Offenbar kann man a = 4.2 aus der Grafik ablesen. Betrachten wir die Funktion f und muiltiplizieren diese aus um sie dann später integrieren zu können:

\begin{aligned} f(x) & = x \cdot (x-a)\cdot (x-6.9) \\ & = x^3 -(a+6.9) x^2 + 6.9ax \\ & = x^3 - 11.1 x^2 + 28.98 x \end{aligned} Damit ergibt sich die Stammfunktion

\begin{aligned} F(x) & = \frac{1}{4}x^4 - \frac{a+6.9}{3} x^3 + 3.45ax^2 + C \\ & = 0.25x^4 - 3.7x^3 + 14.49 x^2 + C \end{aligned}

Um das Intergal \int\limits_{0}^{6.9} g(x)\,\mathrm{d} x zerlegt man das Integral in zwei Teile und nutzt die Tatsache, dass f(x) > 0 für x \in (0, 4.2) und f(x) < 0 für x \in (4.2, 6.9). Damit ergibt sich:

\begin{aligned} \int\limits_{0}^{6.9} g(x)\,\mathrm{d} x & = \int\limits_{0}^{4.2} f(x)\,\mathrm{d} x + \int\limits_{4.2}^{6.9} (-f(x))\,\mathrm{d} x \\ & = \int\limits_{0}^{4.2} f(x)\,\mathrm{d} x - \int\limits_{4.2}^{6.9} f(x)\,\mathrm{d} x \\ & = F(4.2) - F(0) - F(6.9) + F(4.2) \\ & = 2F(4.2) - F(0) -F(6.9) \\ & \approx 46.681 \end{aligned}

a = 4.2
b = 6.9
A = 46.681

Gegeben ist die Funktion f: \mathbb{R} \to \mathbb{R} mit

f(x) = x \cdot (x-a)\cdot (x-b), \quad \text{mit } 0 < a < b. Ferner definieren wir die Funktion g(x) = |f(x)|.

Der Graph zeigt die Funktion g für die Werte a = und b = .

Bestimmen Sie die eingefärbte Fläche A = \int_0^{6.9} g(x)\,\mathrm{d}x =

Offenbar kann man a = 2.4 aus der Grafik ablesen. Betrachten wir die Funktion f und muiltiplizieren diese aus um sie dann später integrieren zu können:

\begin{aligned} f(x) & = x \cdot (x-a)\cdot (x-6.9) \\ & = x^3 -(a+6.9) x^2 + 6.9ax \\ & = x^3 - 9.3 x^2 + 16.56 x \end{aligned} Damit ergibt sich die Stammfunktion

\begin{aligned} F(x) & = \frac{1}{4}x^4 - \frac{a+6.9}{3} x^3 + 3.45ax^2 + C \\ & = 0.25x^4 - 3.1x^3 + 8.28 x^2 + C \end{aligned}

Um das Intergal \int\limits_{0}^{6.9} g(x)\,\mathrm{d} x zerlegt man das Integral in zwei Teile und nutzt die Tatsache, dass f(x) > 0 für x \in (0, 2.4) und f(x) < 0 für x \in (2.4, 6.9). Damit ergibt sich:

\begin{aligned} \int\limits_{0}^{6.9} g(x)\,\mathrm{d} x & = \int\limits_{0}^{2.4} f(x)\,\mathrm{d} x + \int\limits_{2.4}^{6.9} (-f(x))\,\mathrm{d} x \\ & = \int\limits_{0}^{2.4} f(x)\,\mathrm{d} x - \int\limits_{2.4}^{6.9} f(x)\,\mathrm{d} x \\ & = F(2.4) - F(0) - F(6.9) + F(2.4) \\ & = 2F(2.4) - F(0) -F(6.9) \\ & \approx 32.4736 \end{aligned}

a = 2.4
b = 6.9
A = 32.4736