| Nr | Geschlecht | Groesse | Gewicht | Note |
|---|---|---|---|---|
| 1 | männlich | 170 | 73 | gut |
| 2 | männlich | 176 | 69 | befriedigend |
| 3 | männlich | 185 | 80 | sehr gut |
| 4 | männlich | 181 | 76 | sehr gut |
| 5 | weiblich | 169 | 56 | gut |
| 6 | weiblich | 158 | 55 | sehr gut |
| 7 | männlich | 176 | 87 | mangelhaft |
8 Merkmale
Beispiele
Das Gewicht von Studierenden in einem Hörsaal soll untersucht werden. Tabelle 8.1 enthält diese Daten. Die Studierenden sind der Merkmalsträger (eine Zeile), das Gewicht ist das Merkmal (Spalte) und die Ausprägung des Merkmals Gewicht sind z.B. 73 kg.
Die Leistung der Autos eines bestimmten Herstellers sollen verglichen werden. Die verschiedenen Autos sind die Merkmalsträger, die Leistung ist das Merkmal und z.B. 102 kW ist eine Ausprägung des Merkmals.
8.1 Grundgesamtheit, Teilgesamtheit und Stichprobe
Beispiele
Soll das Gewicht nicht nur aller Studierenden in einem Hörsaal sondern aller in Deutschland lebenden Menschen untersucht werden, so ist die Menge aller in Deutschland lebenden Menschen die Grundgesamtheit, die Studierenden in einem Hörsaal bilden eine Stichprobe.
Bei einer Bundestagswahl ist die Menge aller Wähler die Grundgesamtheit. Werden vor den Wahllokalen einige Menschen befragt wie sie gewählt haben, so ist dies eine Stichprobe.
Bemerkungen zu Stichproben:
Offenbar ist die Menge der Studierenden in einem Hörsaal keine gute Stichprobe um eine Aussage über das Gewicht aller in Deutschland lebenden Menschen zu machen. (alle ähnlich alt, ähnliche soziale Schicht, etc.)
Es ist ein Teil der induktiven Statistik, geeignete Stichproben zu nehmen, die Rückschlüsse auf die Grundgesamtheit bzw. die untersuchte Teilgesamtheit zulassen (Repräsentativität). Wirklich repräsentative Umfragen zu machen ist im Allgmeinen schwierig und teuer.
8.2 Skalenniveaus
Die Skalenniveaus der Merkmale legt fest, wie man Merkmale behandelt, das heißt was man mit den Merkmalen machen darf und was nicht. Außerdem legt das Skalenniveau fest wie wir die Merkmale darstellen. Grob unterteilt gibt es zwei verschiedene Skalenniveaus, die kategorialen und die metrischen Merkmale. Man unterscheidet die kategorial skalierten Merkmale nochmal in nominale bzw. ordinale Merkmale. Die metrische skalierten Merkmale in intervallskaliert, verhältnisskaliert oder absolut skaliert.
Kategoriale Skalenniveaus
Nominalskala:
- Bei einer Nominalskala können die Ausprägungen ausschließlich unterschieden werden. (z.B. Geschlecht oder Automarke).
- Zahlen haben nur Bezeichnungsfunktion (z.B. Barcodes, Postleitzahlen, Seriennummern oder Kodierungen wie 0: männlich, 1: weibliche, etc.)
Ordinalskala oder Rangskala:
- Bei einer Ordinalskala (oder auch Rangskala) können die verschiedenen Ausprägungen der Merkmale nur unterschieden und in eine sinnvolle Reihenfolge gebracht werden (z.B. Ränge bei der Armee, eine Likert-Skala oder Noten in einer Klausur)
- Differenzen oder Quotienten sind nicht interpretierbar und Additionen sind unzulässig.
Metrische Skalenniveaus
Kardinalskala oder metrische Skala:
Bei einer Kardinalskala (oder auch metrischen Skala) kann nicht nur eine Reihenfolge hergestellt werden, ferner ist auch ein Abstand zwischen den Ausprägungen sinnvoll (z.B. Körpergröße, Gewinne, Alter, Punkte in einer Klausur)
-
Kardinalskalen können noch feiner unterteilt werden:
Intervallskala: Hier können Differenzen gebildet werden, aber keine Quotienten. Ein Beispiel wäre die Temperatur in Grad Celsius.
Verhältnisskala: Diese ist wie die Intervallskala, es gibt zusätzlich aber einen natürlichen Nullpunkt. Damit können nicht nur Differenzen, sondern auch Quotienten sinnvoll gebildet werden. Beispiele hierfür sind das Barvermögen, die Körpergröße, das Alter oder die Temperatur in Kelvin.
Absolutskala: Diese ist wie die Verhältnisskala, allerdings gibt es zuätzlich noch eine natürliche Einheit in der gemessen wird. Beispiele hierfür sind Anzahlen (z.B. Einwohner eines Landes, Besucher bei einer Sportveranstaltung, Anzahl Studierender einer Hochschule).
| Skalenniveau | Auszählen | Ordnen | Differenzen bilden | Quotienten bilden |
|---|---|---|---|---|
| Nominalskala | ja | nein | nein | nein |
| Ordinalskala | ja | ja | nein | nein |
| Intervallskala | ja | ja | ja | nein |
| Verhältnisskala | ja | ja | ja | ja |
| Absolutskala | ja | ja | ja | ja |
Selbsttest: Skalenniveaus
Welches Skalenniveau hat das Merkmal Bücher in einer Bibliothek
Welches Skalenniveau hat das Merkmal IQ
Welches Skalenniveau hat das Merkmal Richter Skala (Erdbeben)
Welches Skalenniveau hat das Merkmal Postleitzahlen
Welches Skalenniveau hat das Merkmal Gänge an einem Fahrrad
Welches Skalenniveau hat das Merkmal Datum
Welches Skalenniveau hat das Merkmal Jahresgehalt
Welches Skalenniveau hat das Merkmal Karatzahl eines Diamanten
Welches Skalenniveau hat das Merkmal Karatzahl eines Diamanten
Welches Skalenniveau hat das Merkmal Karatzahl eines Diamanten
Welches Skalenniveau hat das Merkmal Länge einer Radfahrt
Welches Skalenniveau hat das Merkmal Dividende einer Aktie
Welches Skalenniveau hat das Merkmal Likert-Skala
Welches Skalenniveau hat das Merkmal Telefonnummern
Welches Skalenniveau hat das Merkmal ELO-Zahl (Schach)
Welches Skalenniveau hat das Merkmal Telefonnummern
Welches Skalenniveau hat das Merkmal Jahresgehalt
Welches Skalenniveau hat das Merkmal Temperatur in Kelvin
Welches Skalenniveau hat das Merkmal IQ
Welches Skalenniveau hat das Merkmal Jahresgehalt
Welches Skalenniveau hat das Merkmal Gefahrenskala (z.B. für Lawinen)
Welches Skalenniveau hat das Merkmal Altersklassen (z.B. Leichtathletik)
Welches Skalenniveau hat das Merkmal Frequenz eines Tons
Welches Skalenniveau hat das Merkmal Gänge an einem Fahrrad
Welches Skalenniveau hat das Merkmal Studiengang
Welches Skalenniveau hat das Merkmal Jahresgehalt
Welches Skalenniveau hat das Merkmal Schulnoten (1 bis 6)
Welches Skalenniveau hat das Merkmal Einkommenklassen
Welches Skalenniveau hat das Merkmal Bevölkerung eines Landes
Welches Skalenniveau hat das Merkmal Gänge an einem Fahrrad
8.3 Diskrete und stetige Merkmale
Eine simple Unterteilung der Merkmale orientiert sich an den möglichen Ausprägungen, die ein Merkmal haben kann.
Beispiele:
-
Abzählbare Merkmale sind immer diskret. Dabei darf es sogar abzählbar unendlich viele verschiedene Ausprägungen geben:
- die Anzahl der Würfe bis man mit zwei sechsseitigen Würfeln einen Sechserpasch würfelt, oder
- die Anzahl der abgegebenen Tipps bis man beim Lotto 6 Richtige hat.
Das Vermögen ist quasi-stetig, da es nur bis auf einen Cent genau angegeben werden kann.
Die Rendite einer Aktie ist hingegen stetig, da man sie theoretisch auf beliebig viele Stellen hinter dem Komma berechnen kann.
Bemerkung:
Quasi-stetige Merkmale werden in der Regel wie stetige Merkmale behandelt.
8.4 Klassieren von Daten
Bei stetigen oder auch quasi-stetigen Daten ist es oft sinnvoll diese zu Klassen zusammenzufassen und damit wie ein diskretes Merkmal aussehen zu lassen. Beispiele hierfür sind Einkommen, Mieten, Noten bei Klausuren oder Altersklassen beim Sport.
| Einkommen | Frauen | Männer | Alle |
|---|---|---|---|
| Kein Einkommen | 10.6 | 5.1 | 7.9 |
| (0; 500) Euro | 10.5 | 4.5 | 7.5 |
| [500; 1000) Euro | 22.4 | 10.6 | 16.6 |
| [1000; 1500) Euro | 23.5 | 16.4 | 20.0 |
| [1500; 2000) Euro | 14.9 | 18.5 | 16.6 |
| [2000; 2500) Euro | 9.2 | 17.0 | 13.0 |
| [2500; 3000) Euro | 3.9 | 8.4 | 6.1 |
| [3000; 3500) Euro | 1.8 | 5.7 | 3.7 |
| [3500; 4000) Euro | 1.2 | 4.0 | 2.6 |
| [4000; 4500) Euro | 0.8 | 3.2 | 2.0 |
| [4500; 5000) Euro | 0.5 | 2.2 | 1.4 |
| Über 5000 Euro | 0.6 | 4.4 | 2.5 |
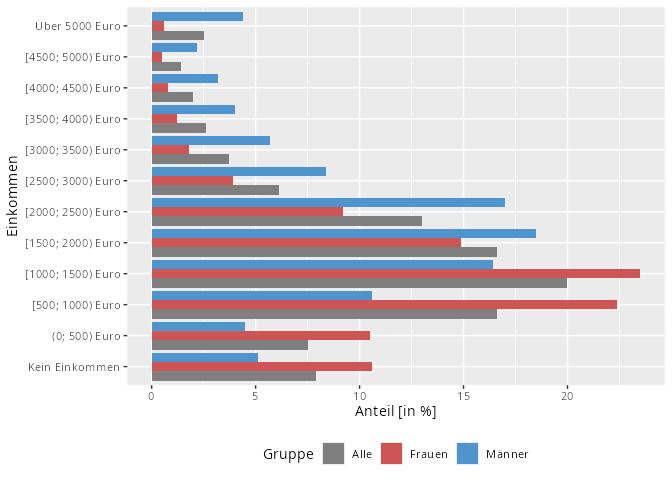
Außerdem können Darstellungen übersichtlicher werden: Bei der oberen Erhebung zum Einkommen wurden zum Beispiel insgesamt 23.299 Leute befragt. Diese werden nicht alle einzeln aufgeführt, sondern müssen, um sie tabellarisch darstellen zu können, klassiert werden. Durch die Klassierung oben erreicht man auch, dass die Ausreißer, also Menschen, die sehr sehr viel mehr als 5000 Euro verdienen auch sinnvoll in einer Grafik abgebildet werden können. Dies wäre bei einem Histogramm, der Alternative zu den Klassen, nicht gegeben.
Ein weiterer praktischer Grund für eine Klassierung könnte sein, dass Beobachtungen, die in eine Klasse fallen auch gleich behandelt werden. So zum Beispiel Altersklassen im Sport, die dazu dienen einen faireren Wettkampf zu ermöglichen.
8.5 Visualisierung
Die Wahl der Grafik hängt von mehreren Faktoren ab:
Wie viele Merkmale sollen in der Grafik dargestellt werden?
Welches Skalenniveau hat das Merkmal / haben die Merkmale, die dargestellt werden sollen?
Welchen Aspekt der Daten möchte ich mit meiner Grafik betonen?
Dieses Kapitel hat zwei Ziele: zum einen werden wir eine Übersicht über wichtige Grafiken geben und zum anderen soll aufgezeigt werden wie man diese Grafiken, in der einfachsten Form, mit dem Paket ggplot2 erstellen kann. Wir werden in Kapitel 16 und Kapitel 17 noch genauer auf das Erstellen der jeweiligen Grafik eingehen und darauf wie diese zu interpretieren ist. Insbesondere wenn statistische Transformationen (zum Beispiel bei Histogramm, Boxplot oder Mosaikplots) durchgeführt werden müssen, ist die Interpretation der Grafiken nicht immer trivial. In den späteren Kapiteln legen wir das Augenmerk insbesondere auf die Syntax, wie man Grafiken ändert (Farbgebung, Anordnungen, verschiedene geometrische Funktion, Ändern der Legende und der Achsen, und so weiter).
Weitere Anregungen zu Grafiken findet man in der R Graph Gallery und eine kompakte Übersicht im ggplot2 Cheat Sheet.
8.5.1 Ein Merkmal: kategorial
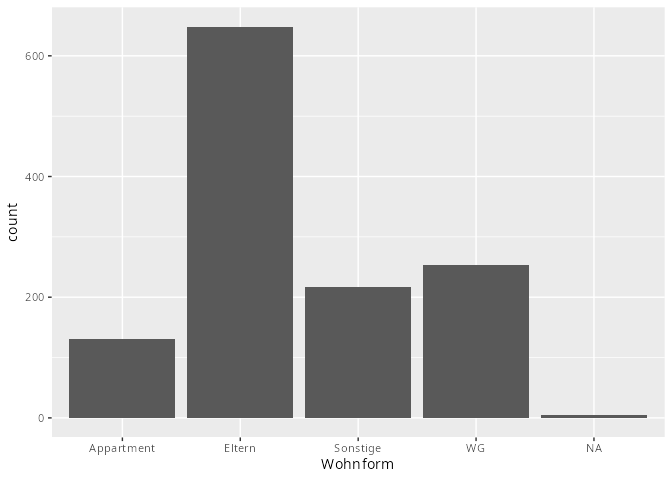
Um kategorial skalierte Merkmale (auch qualitative Merkmale genannt) darzustellen verwenden wir Säulen- oder Balkendiagramme. Die geometrische Funktion dafür ist geom_bar().
Bemerkung: In der Regel ist die Anzahl der Ausprägungen überschaubar. Sollte die Anzahl doch größer sein, bietet das Paket forcats Möglichkeiten das zu beheben.
penguins |>
ggplot(aes(x = species)) +
geom_bar()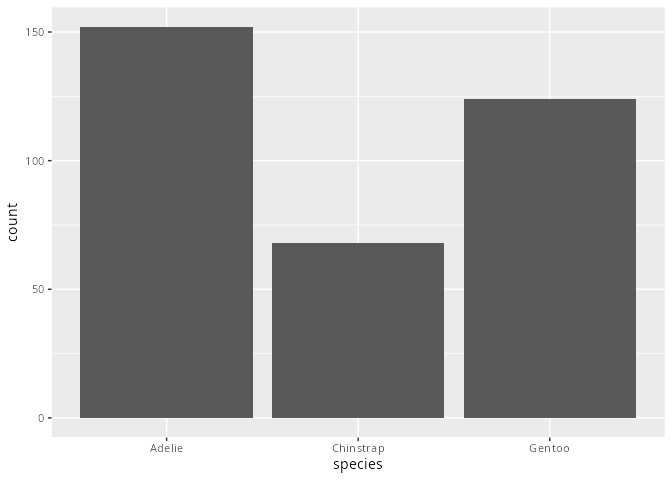
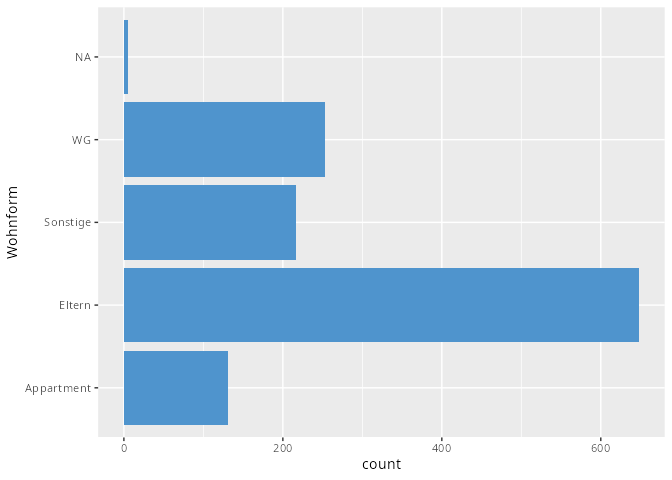
penguins |>
ggplot(aes(y = species)) +
geom_bar()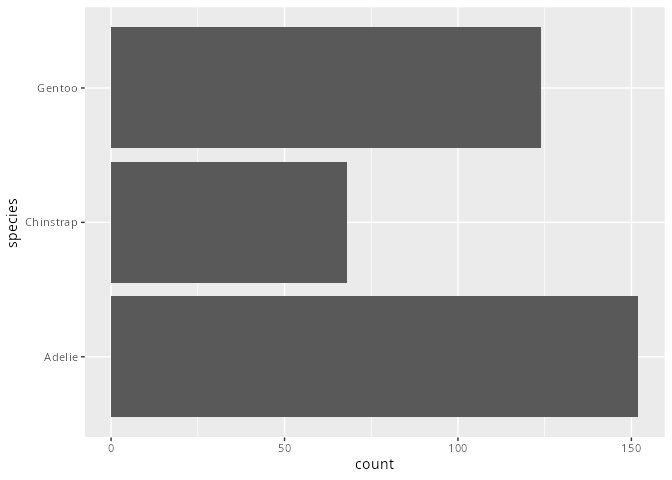
Die Anordnung der Säulen oder Balken erfolgt bei einem nominalen Merkmal alphabetisch. Möchte man eine bessere Lesbarkeit der Daten erreichen, so kann man die Reihenfolge mit Hilfe von Funktionen aus dem Paket forcats (Kapitel 15) ändern. Zum Beispiel wird in Abbildung 9.3 das Merkmal species in absteigender Häufigkeit dargestellt.
penguins |>
ggplot(aes(x = fct_infreq(species))) +
geom_bar()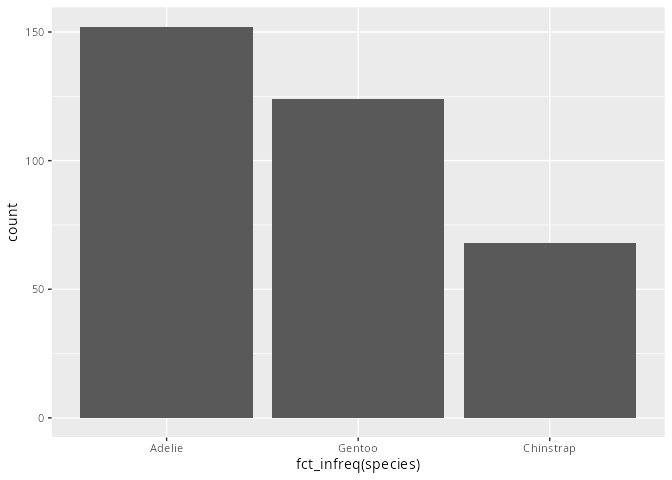
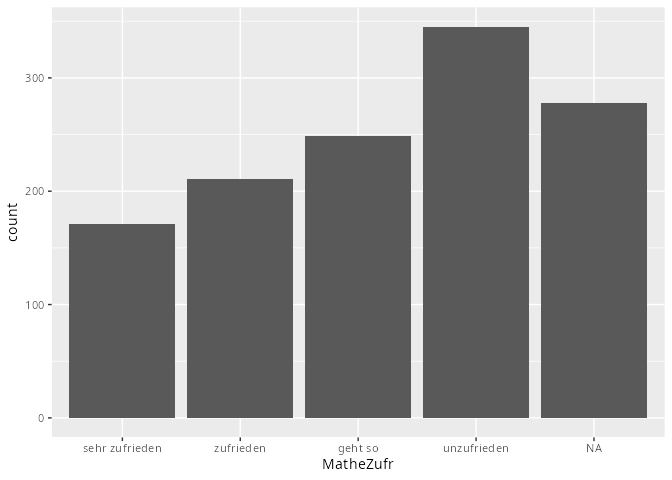
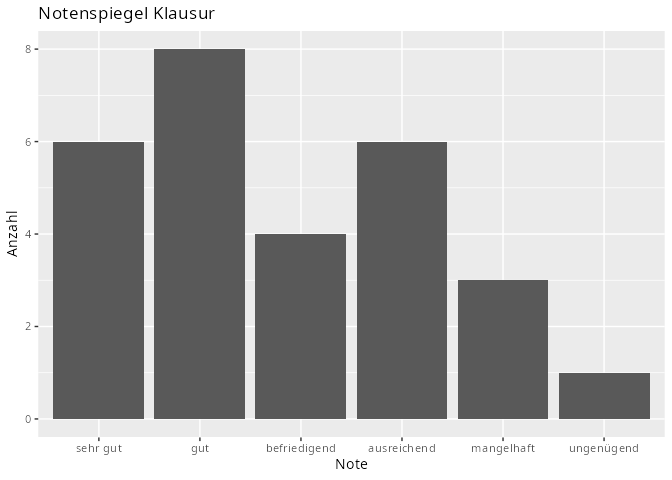
Handelt es sich um ein ordinales Merkmal (in R ein ordinaler Faktor, der in Datentabellen mit <ord> gekennzeichnet ist), so ist die Ordnung die natürliche Ordnung in der die Säulen oder Balken angeordnet werden.
8.5.2 Ein Merkmal: metrisch
Metrische Merkmale (auch quantitative Merkmale genannt) können ein Spektrum von Werten annehmen. Bei metrischen Merkmalen ist es ist sinnvoll Differenzen zu bilden und statistische Größen wie Mittelwerte, zu berechnen.
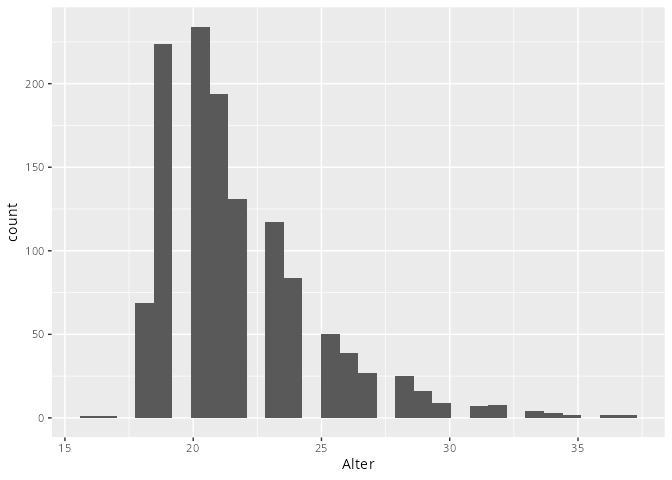
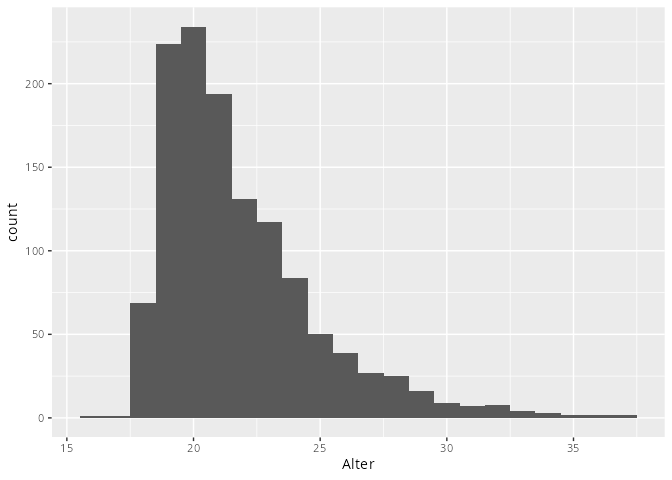
Histogramm
Die übliche Darstellung eines solchen Merkmals ist das Histogramm. Die geometrische Funktion hierzu ist geom_histogram().
penguins |>
ggplot(aes(x = body_mass_g)) +
geom_histogram(binwidth = 200,
fill = "steelblue3",
color = "grey30")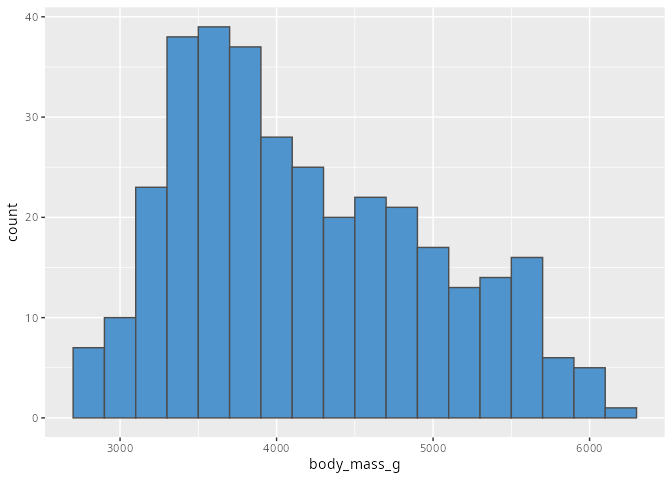
penguins |>
ggplot(aes(x = body_mass_g)) +
geom_histogram(binwidth = 20,
fill = "steelblue3",
color = "grey30")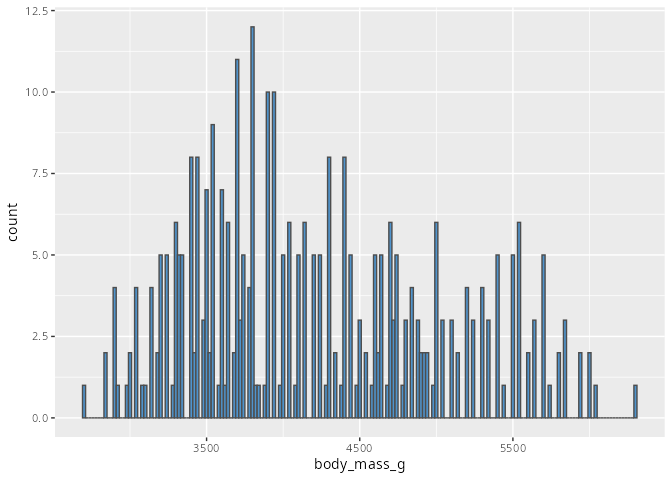
penguins |>
ggplot(aes(x = body_mass_g)) +
geom_histogram(binwidth = 1000,
fill = "steelblue3",
color = "grey30")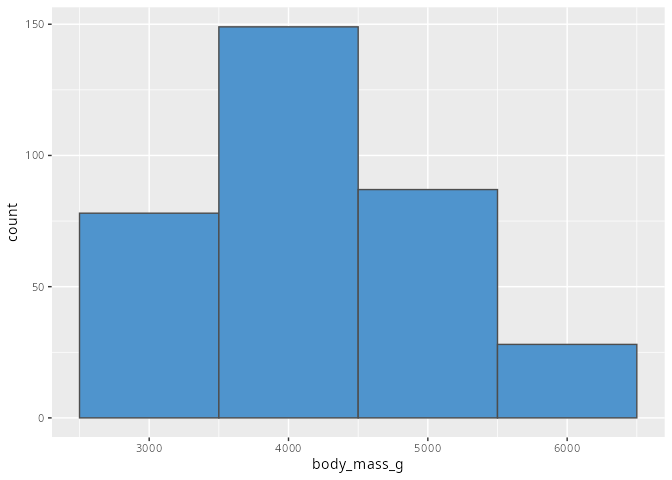
Bei einem einfachen Histogramm werden gleichbreite Klassen gebildet und die Anzahl der Elemente innerhalb einer Klasse wird auf der y-Achse aufgetragen. Die Breite ist von der Wahl des Arguments binwidth= abhängig. Alternativ kann auch die Anzahl der Balken angegeben werden; dies geschieht mit dem Argument bins=. Gibt man keines der beiden Argumente an, so werden 30 Säulen gebildet, wobei nicht jede Säule unbedingt Einträge haben muss. Welche Wahl sinnvoll ist hängt von der Fragestellung ab: um einen groben Überblick über die Verteilung zu bekommen sollte die Balkenbreite weder zu klein (Abbildung 8.9) noch zu groß (Abbildung 8.10) gewählt werden. Wir werden in Kapitel 17 im Rahmen der explorativen Datenanalyse noch einmal darauf zurückkommen.
Bemerkung:
Histogramme haben im Gegensatz zu den Säulen- und Balkendiagrammen eine kontinuierliche Skala. So kann man selbst, wenn die Ausprägungen der Merkmale nur diskrete Werte annehmen, bei metrischen Merkmalen Mittelwerte oder Quantile bestimmen und ebenfalls sinnvoll in ein Histogramm einzeichnen.
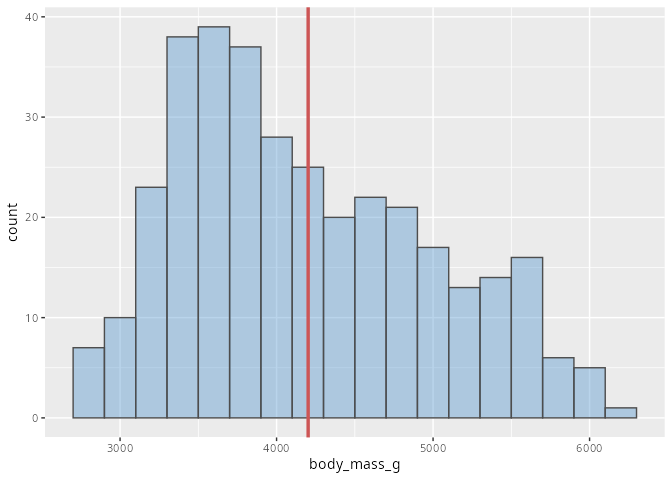
Boxplot
Eine weitere Möglichkeit ein metrisches Merkmal darzustellen ist ein Boxplot. Er liefert einen schnellen Überblick über die Daten.
Die Linie im inneren der Box ist der Median der Daten. Dies heißt 50% der Daten sind kleiner oder gleich des Medians und 50% der Datenpunkte sind gleich oder größer des Medians.
Die Box enhält die mittelren 50% der Daten.
Die Whisker und ggf. Ausreißer geben die kleinsten und größten Werte an.
Die genaue Definition und eine ausführliche Erklärung ist in Kapitel 17.3.1 zu finden.
penguins |>
ggplot(aes(x = body_mass_g)) +
geom_boxplot(fill = "steelblue3",
color = "grey30",
alpha = 0.3) +
scale_y_continuous(NULL, breaks = NULL) # keine Beschriftung y-Achse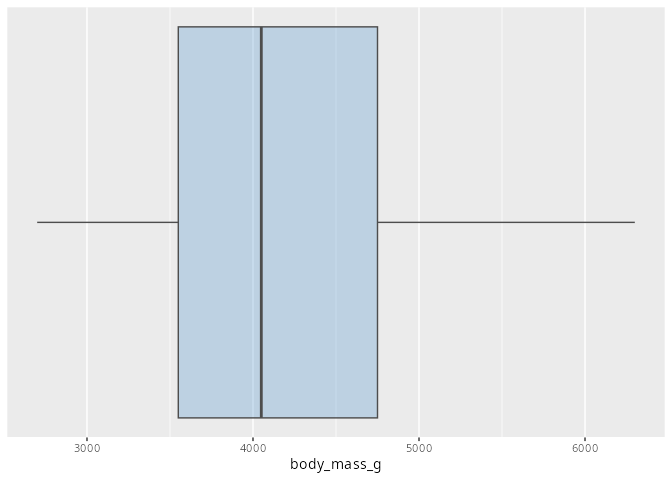
Häufigkeitspolygon
Häufigkeitspolygone sind eng mit den Histogrammen verbunden. Sie werden so konstruiert, dass die Mitten der oberen Enden der Säulen durch einen Polygonzug mit den direkten Nachbarn verbunden werden. Der große Vorteil dieser Darstellung ist, dass so mehrere Verteilungen gleichzeitig in ein Diagramm gezeichnet werden können. Aufgrund von Überlappungen ist dies bei Histogrammen normalerweise nicht möglich.
penguins |>
ggplot(aes(x = body_mass_g)) +
geom_histogram(binwidth = 300,
fill = "steelblue3",
color = "grey30",
alpha = 0.4) +
geom_freqpoly(binwidth = 300,
color = "indianred3",
linewidth = 1.3)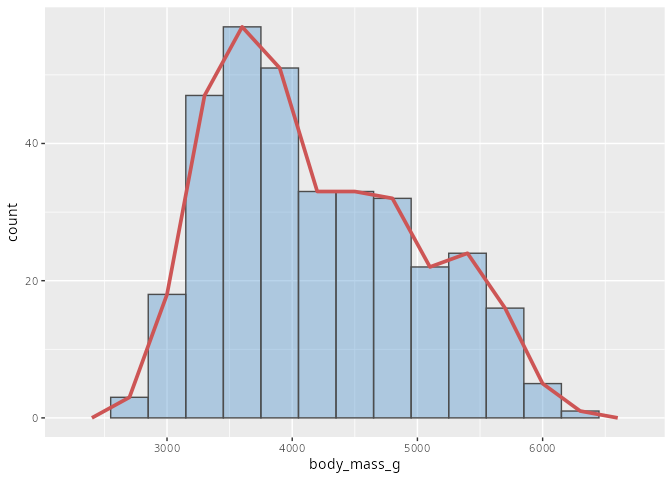
Dichtediagramm
Eine andere Darstellung eines metrischen Merkmals ist ein Dichtediagramm. Ein Dichtediagramm ist eine geglättete und normierte Version des Histogramms bzw. des Häufigkeitspolygons. Wie diese Glättung genau funtioniert soll hier nicht weiter ausgeführt werden, kann aber im der Hilfe zur geometrischen Funktion geom_density() nachgelesen werden.
penguins |>
ggplot(aes(x = body_mass_g)) +
geom_density(linewidth = 1.2, color ="steelblue3")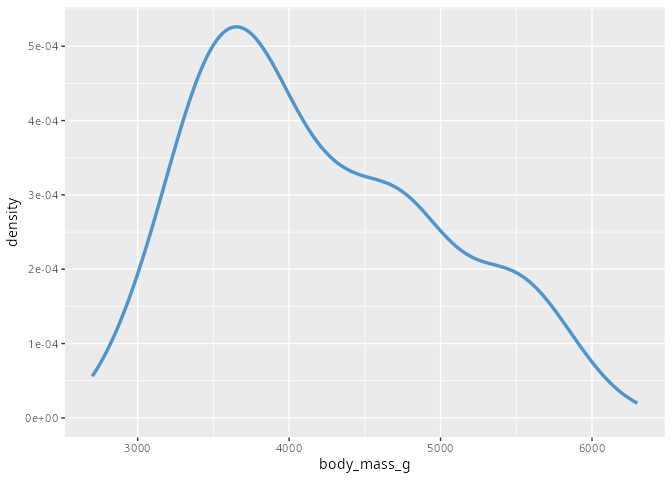
8.5.3 Zwei Merkmale: metrisch / metrisch
Streudiagramm
Das Streudiagramm haben wir in Kapitel 3.2 schon kennengelernt. Die geometrische Funktion ist geom_point().
penguins |>
ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
geom_point()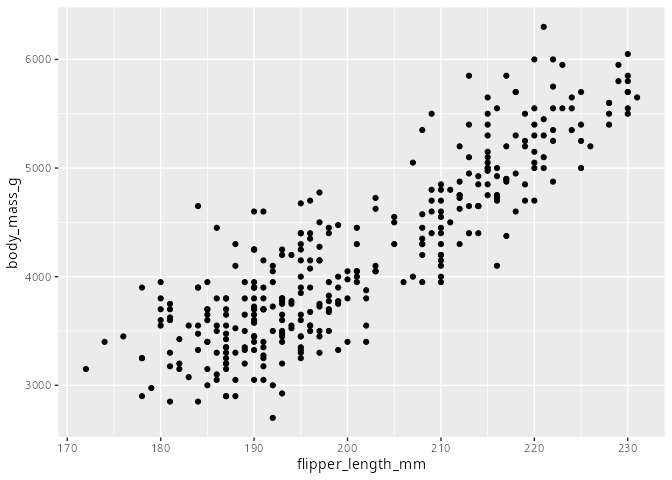
8.5.4 Zwei Merkmale: kategorial / metrisch
Boxplot
Den Boxplot haben wir bereits kennengerlent. Es ist möglich dem Boxplot nicht nur ein metrisches Merkmal zu übergeben, sondern zusätzlich auch ein kategoriales.
Das Ergbnis ist, dass für jede Ausprägung des nominalen Merkmals ein eigener Boxplot erstellt wird. Je nachdem welcher Koordinate man das metrische Merkmal zugeordnet hat entstehen horizontale oder vertikale Boxplots. Die Breite der so erstellten Boxplots hat keine Bedeutung.
penguins |>
ggplot(aes(x = species, y = bill_length_mm)) +
geom_boxplot()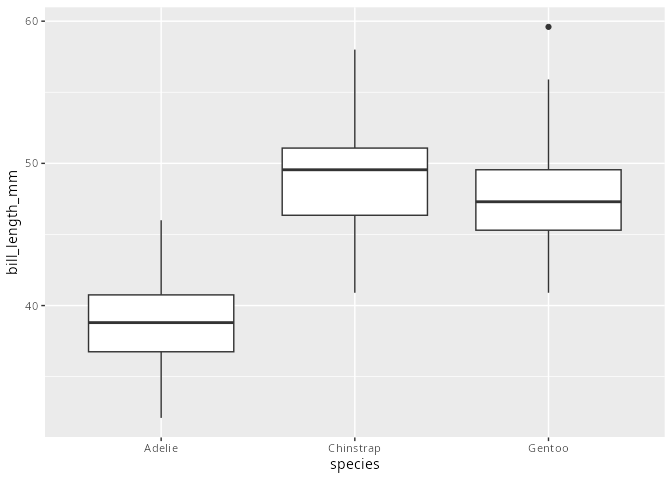
Violinenplot
Violinenplots sind von der Syntax und der Visualisierung den Boxplots sehr ähnlich. Allerdings liegt das Augenmerk bei den Violinenplots auf der Verteilung der Ausprägungen des metrischen Merkmals.
penguins |>
ggplot(aes(x = species, y = bill_length_mm)) +
geom_violin()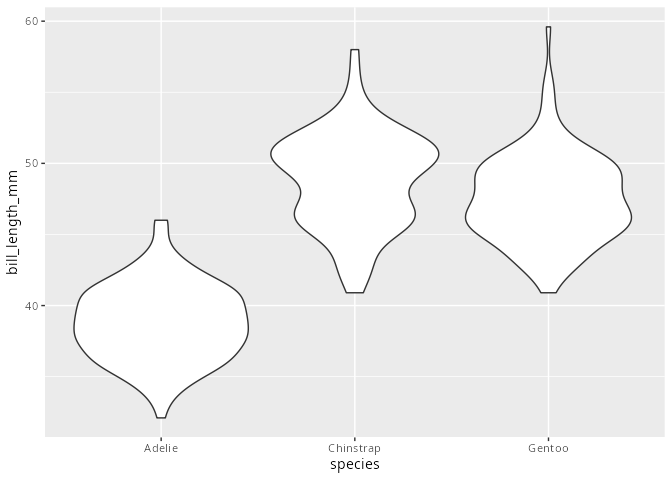
Die maximale Breite des Violinenplots ist unabhängig von der Anzahl der Beobachtungen. Allerdings hat der Violinenplot auch interessante Argumente
Ändert man
scale = "area"aufscale = "count", so wird die Fläche auf die repräsentierte Anzahl skaliert.Mit dem Argument
draw_quantile=können beliebiege Quantile eingezeichnet werden.
penguins |>
ggplot(aes(x = species, y = bill_length_mm)) +
geom_violin(scale = "count", draw_quantiles = c(0.25, 0.5, 0.75))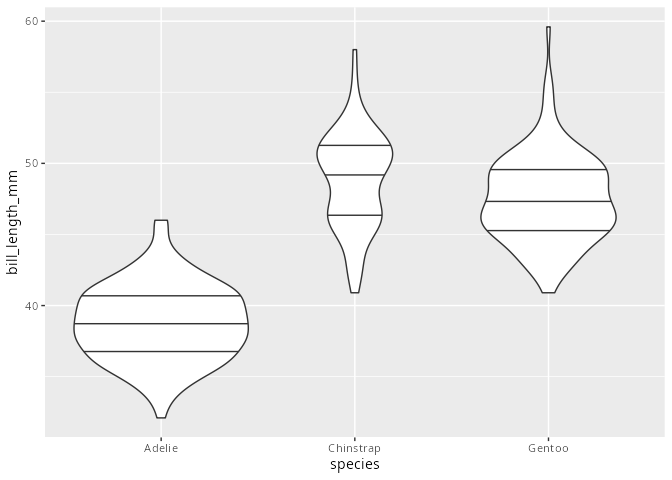
Häufigkeitspolygon
penguins |>
ggplot(aes(x = bill_length_mm, color = species)) +
geom_freqpoly(bins = 30)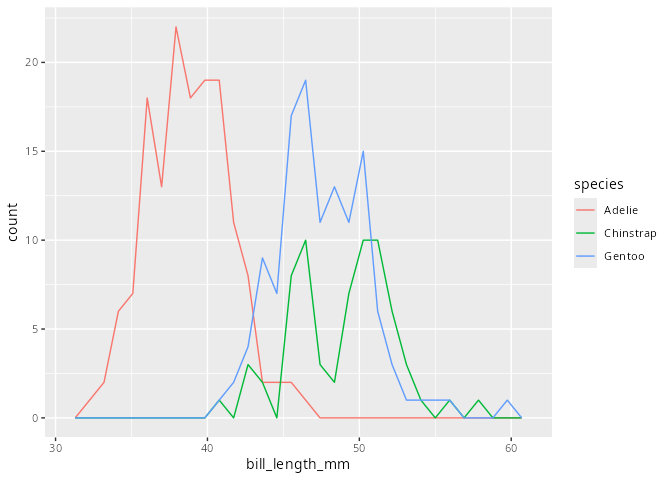
Dichtediagramme
penguins |>
ggplot(aes(x = bill_length_mm, color = species)) +
geom_density()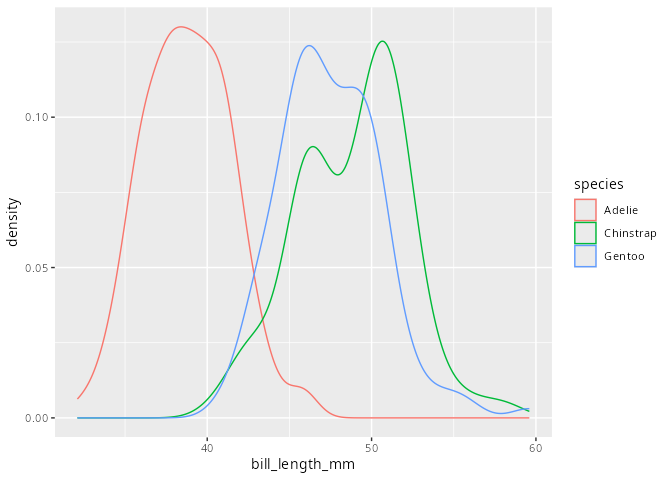
Es ist zu bemerken, dass die jeweiligen Dichten pro Ausprägung des kategorialen Merkmals genommen werden.
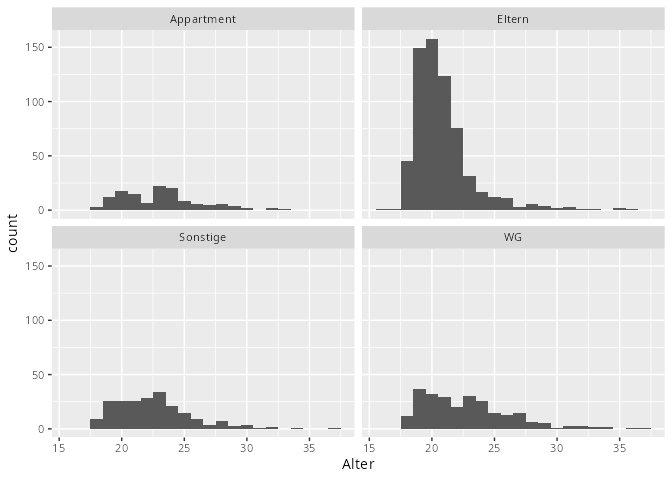
Facettierte Histogramme
penguins |>
ggplot(aes(y = bill_length_mm)) +
geom_histogram() +
facet_wrap(~species)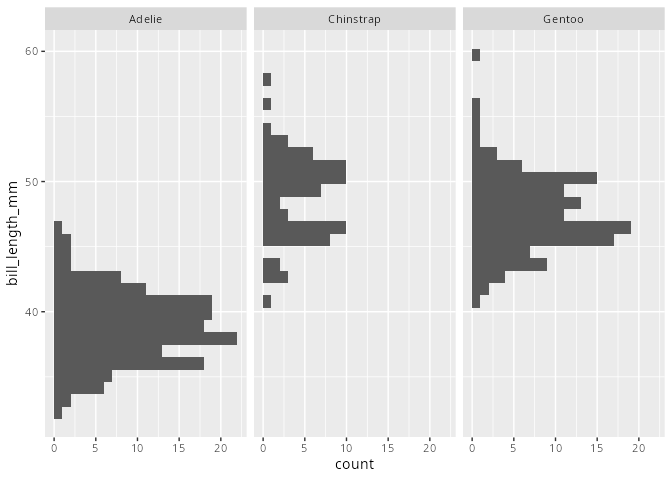
8.5.5 Zwei Merkmale: kategorial / kategorial
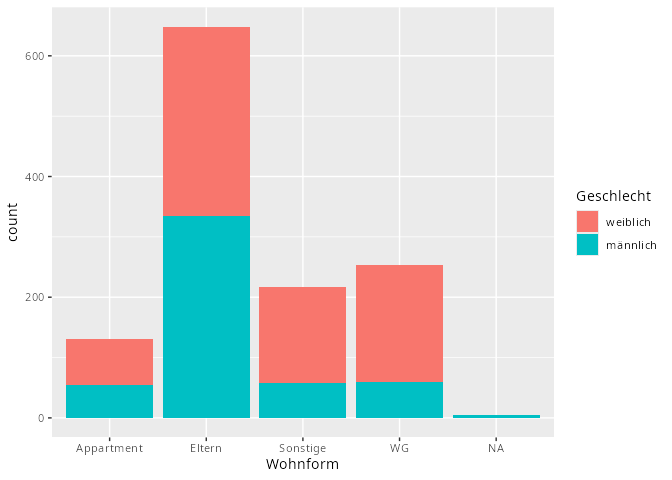
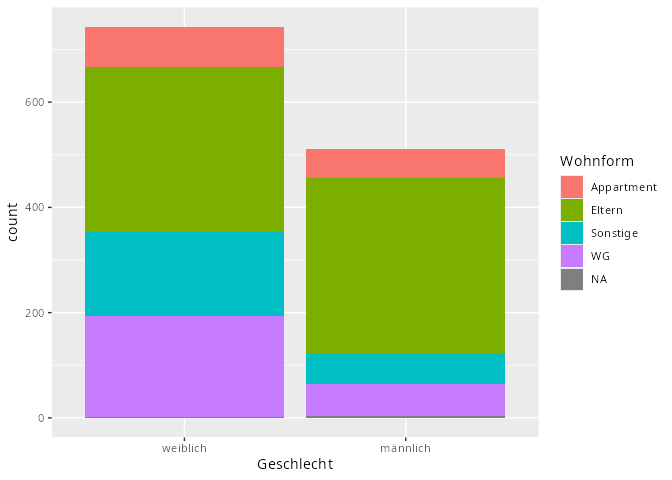
Säulen- oder Balkendiagramme
penguins |>
ggplot(aes(x = island,
fill = species)) +
geom_bar() 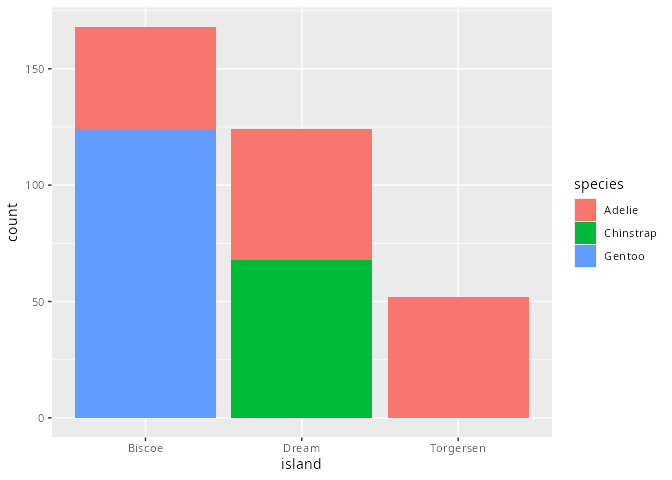
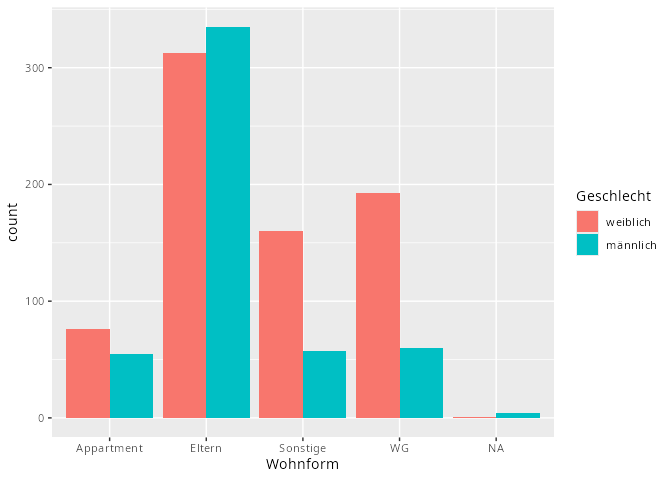
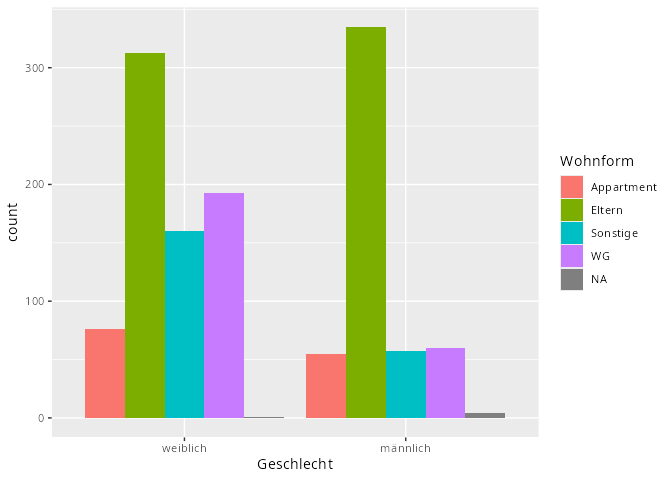
penguins |>
ggplot(aes(x = island,
fill = species)) +
geom_bar(position = "dodge") 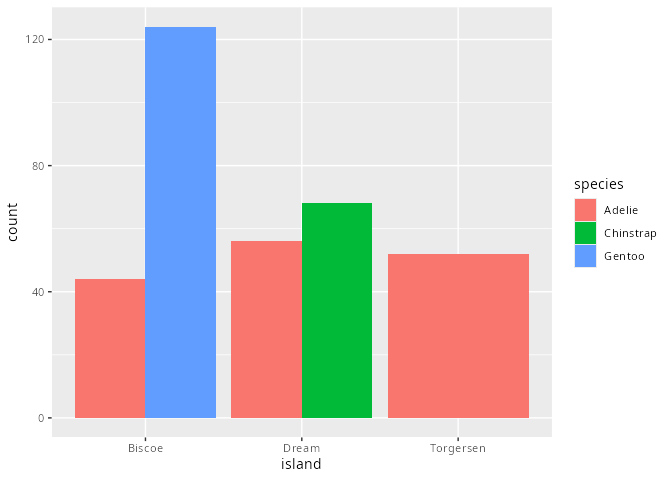
Mosaikdiagramm
Das Mosaikdiagramm (oder Mosaikplot) ist eine weitere Möglichkeit zwei kategoriale Merkmale gleichzeitig zu zeigen. Hierbei repräsentieren Breite bzw. Höhe der Ausprägungen deren relativen Anteil aller Ausprägungen. Die Flächen der entstehenden Rechtecke sind dann der relative Anteil der kombinierten Beobachtungen.
Der Mosaikplot eignet sich besonders gut umd die (Un-)abhängigkeit verschiedener Merkmalen voneinander sichtbar zu machen.