7 Gebiete der Statistik
Deskriptive Statistik (beschreibende / empirische Statistik):
Ziel ist es empirische Daten, das sind Daten aus Experimente, Erhebungen oder Umfragen etc., durch Grafiken, Maßzahlen / Kennzahlen und Tabellen darzustellen.
Induktive Statistik (schließende / inferentielle / mathematische Statistik):
In vielen Szenarien stehen nicht alle vorhandenen Daten zur Verfügung (Stichproben). Das Ziel der induktiven Statistik besteht darin aus den zur Verfügung stehenden Daten Informationen über alle Daten, der Grundgesamtheit bzw. der Teilgesamtheit, zu erlangen. Grundlage hierfür ist die Wahrscheinlichkeitstheorie.
Explorative Statistik (explorative Datenanalyse):
Ziele bestehen darin Zusammenhänge in Daten zu finden, um Gründe für die jeweiligen Beobachtungen zu finden und diese mit geeigneten statistischen Methoden weiter zu untersuchen, sowie eine Grundlage für zukünftige Untersuchungen (z.B. Umfragen oder statistische Versuchsplanung) zu schaffen.
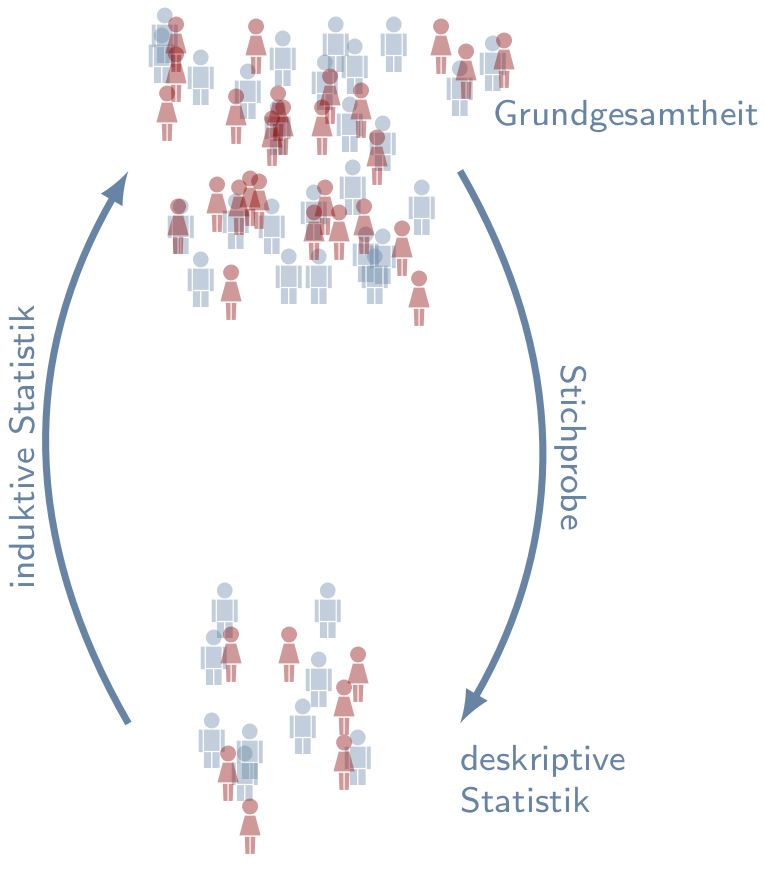
Wir wollen anhand eines Beispiels die Unterschiede zwischen der deskriptiven und der induktiven Statistik erläutern:
Beispiel:
Es werden 30 Studenten eines Jahrgangs befragt wie lange sie sich in der Woche mit Mathematik beschäftigen.
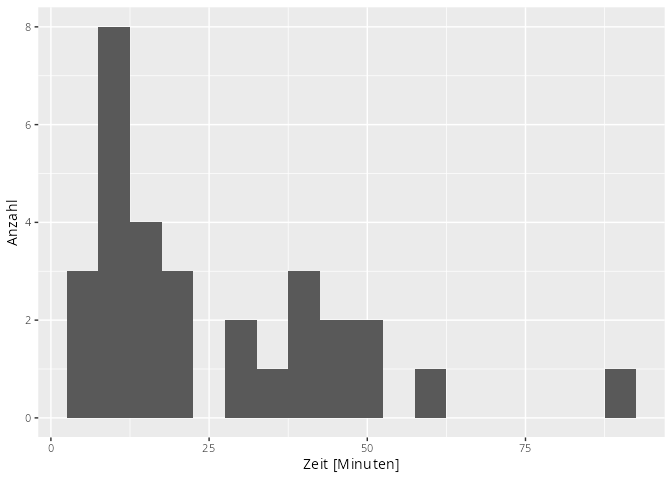
Es ergaben sich die folgenden Antworten. Dabei steht in der oberen Zeile die Antwort in Minuten und in der zweiten Zeile steht wie viele der Studenten diese Antwort gegeben haben.
| Zeit[min] | 5 | 10 | 15 | 20 | 30 | 35 | 40 | 45 | 50 | 60 | 90 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl | 3 | 8 | 4 | 3 | 2 | 1 | 3 | 2 | 2 | 1 | 1 |
Deskriptive Statistik:
Für Menschen ist es im Wesentlichen unmöglich Datentabelle sinnvoll zu erfassen und Zusammenhänge zu sehen, insbesondere wenn die Datentabellen groß werden. Aufgabe der deskriptiven Statistik ist es nun die Daten in eine für Menschen verdauliche Form zu bringen. Dazu werden zum einen statsitiche Kenngrößen berechnet und zum anderen Daten visualisiert.
- Einige Kenngrößen, die man aus den obigen Daten bestimmen kann wären zum Beispiel:
| Statistische Größe | Wert [in Minuten] |
|---|---|
| Minimum | 5 |
| Maximum | 90 |
| Spannweite | 85 |
| Modus | 10 |
| 25% Quantil | 10 |
| 50% Quantil / Median | 17.5 |
| 75% Quantil | 40 |
| Arithmetisches Mittel | 25.67 |
| Standardabweichung | 19.49 |
- Um diese Daten dann grafisch darzustellen nutzt man in diesem Fall zum Beispiel
Histogramme oder

Boxplots.
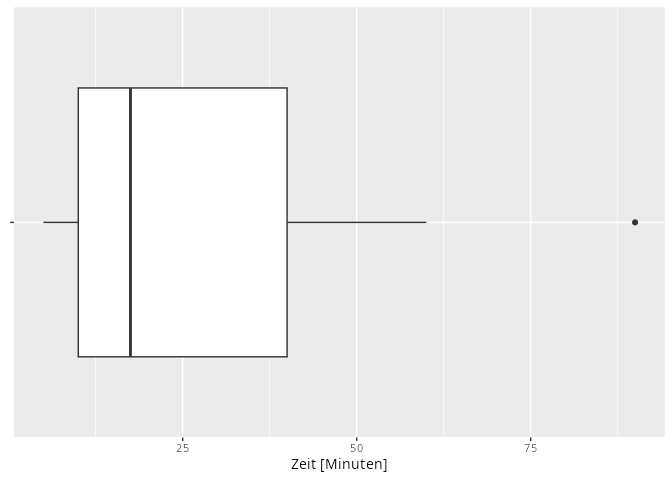
Was die einzelnen Kenngrößen bedeuten, wie man diese berechnet und welche Grafiken bei welchen Daten genutzt werden, ist ein wichtiger Aspekt dieses Kurses und wird in späteren Kapitel noch ausführlich behandelt.
Induktive Statistik:
Im Gegensatz dazu möchte man mit Hilfe der induktiven Statistik Aussagen über die Grundgesamtheit, zum Beispiel alle Studenten des Studiengangs oder alle Studenten der Hochschule treffen. In obigen Beispiel wäre zum Beispiel eine mögliche Fragestellungen:
“Wie lange beschäftigen sich alle Studenten des Jahrgangs / des Studiengangs im Durchschnitt wöchentlich mit Mathematik?”
Die Antwort darauf lautet dann zum Beispiel
Mit 95 prozentiger Sicherheit beschäftigen sich die Studenten im Mittel zwischen 18.1 und 33.2 Minuten mit Mathematik.
oder
Mit 99 prozentiger Sicherheit beschäftigen sich die Studenten im Mittel zwischen 15.5 und 35.8 Minuten mit Mathematik.