14 Explorative Datenanalyse

14.1 Was ist Explorative Datenanalyse (EDA)?

Idee: Bei der explorativen Datenanalyse, kurz EDA, geht es darum, einen Datensatz zu untersuchen und zu analysieren.

Methode: EDA ist kein formaler Prozess mit strikt vorgegebenen Regeln, sondern eine iterative Vorgehensweise:

Man überlegt sich Fragen zu den Daten
Versuche, diese Fragen mit Visualisierungen, Transformationen und Modellen zu beantworten.
Nutze die Erkenntnisse, um die Fragen zu konkretisieren und um neue Fragen zu formulieren.

Ziel: Irgendwann muss man entscheiden und kommunizieren, ob die Daten die gestellten Fragen beantworten können oder nicht. Die Qualität der Daten spielt dabei eine entscheidende Rolle. Die EDA dient auch dazu, eine möglichst gute Datenqualität herzustellen.

Begriffe

Merkmal ist eine Eigenschaft, die man qualitativ (nominal oder ordinal) oder quantitativ (metrisch) messen kann.
Eine Ausprägung oder ein Wert ist ein Zustand, den ein Merkmal bei einer Messung angenommen hat. Die Ausprägung kann je nach Messung unterschiedlich sein.
Eine Beobachtung oder ein Datenpunkt ist eine Menge von Messungen, die unter ähnlichen Bedingungen gemacht wurden. Eine Beobachtung kann mehrere Werte zu verschiedenen Merkmalen enthalten.
Eine Datentabelle ist eine rechteckige Ansammlung von Werten, wobei jeder Wert einem Merkmal zugeordnet ist. Eine Datentabelle ist bereinigt (tidy), falls jede Ausprägung eine eigene Zelle hat, jedes Merkmal eine eigene Spalte und jede Beobachtung eine eigene Zeile.

Der Weg zu einer bereinigten Datentabelle ist in der Praxis steinig und macht häufig den Hauptteil der Arbeit aus.

Fragen

Untersucht man Daten so drängen sich zwei Fragen auf:

Wie variieren die Daten innerhalb eines Merkmals? (Variation).
Gibt es einen Zusammenhang zwischen verschiedenen Merkmalen? (Kovariation)

In den folgenden Kapiteln sollen die notwendigen Mittel um diese Fragen graphisch zu untersuchen, vorgestellt werden.

14.2 Variation

14.2.1 Kategoriale Merkmale

Bei einem kategorialen Merkmal nimmt das Merkmal meist nur eine relativ kleine Anzahl von Werten an, mit denen man nicht (sinnvoll) rechnen kann, wie z.B. Automarken, Postleitzahlen oder Farben. In R sind kategoriale Merkmale als Faktor (<fct>), geordnete Faktoren (<ord>) oder als Zeichenkette (<chr>) hinterlegt. Um die Verteilung eines kategorialen Merkmals zu untersuchen, ist die neheliegende Grafik das Säulendiagramm oder Balkendiagramm.

# Anzahl der Beobachtungen für cut:
diamonds |> count(cut)

# A tibble: 5 × 2
  cut           n
  <ord>     <int>
1 Fair       1610
2 Good       4906
3 Very Good 12082
4 Premium   13791
5 Ideal     21551

diamonds |> 
   ggplot(aes(x = cut)) + 
   geom_bar()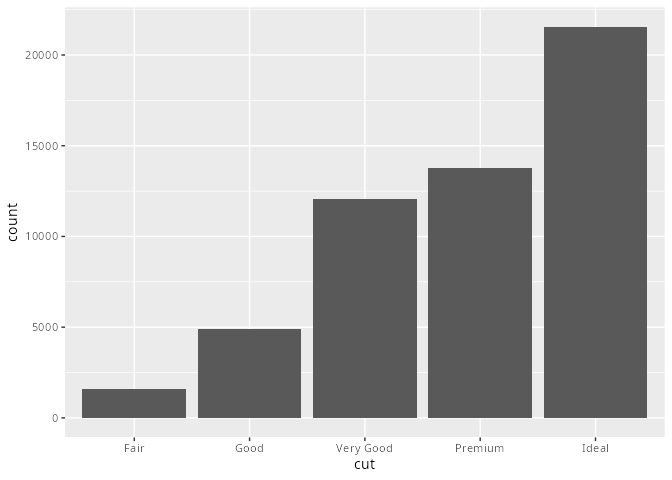

Abbildung 14.1: Säulendiagramm für das kategoriale Merkmal `cut` aus dem Satensatz `diamonds`.

14.2.2 Metrische Merkmale

Ein metrisches Merkmal kann (theoretisch) unendlich viele Zahlenwerte annehmen, mit denen man rechnen kann, z.B. Längen, Alter oder Anzahlen. Eine geeignete Darstellung solcher Merkmale sind Histogramme. Dabei teilt man den Wertebereich des Merkmals in (häufig gleich breite) Intervalle ein. Dies geschieht in der Funktion geom_histogram().

diamonds |> 
   ggplot(aes(x = carat)) + 
   geom_histogram(binwidth = 0.5)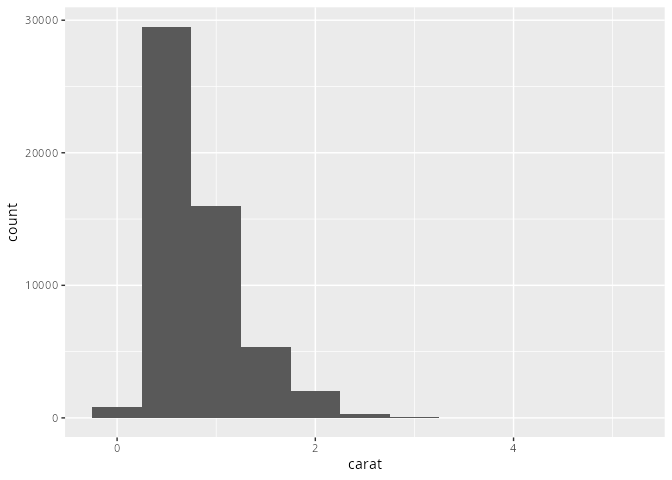

Abbildung 14.2: Histogramm des Merkmals `carat`. Die Breite der Säulen wird durch das Argument `binwidth=0.5` festgelegt.

Mit dem Argument binwidth= kann die Breite der Balken des Histogramms festgelegt werden. Die Höhe der darüber gezeichneten Rechtecke entspricht der Häufigkeitsdichte der Beobachtungen in dem jeweiligen Intervall. Wenn die Intervalle alle gleich breit sind, entspricht dies der absoluten oder relativen Häufigkeit (siehe Kapitel 8.7).

Ein Variieren der Werte für des Argument binwidth= kann dazu führen, dass neue Muster offen gelegt werden.

smaller <- diamonds |> filter(carat < 3)

smaller |> 
     ggplot(aes(x = carat)) +
     geom_histogram(binwidth = 0.1)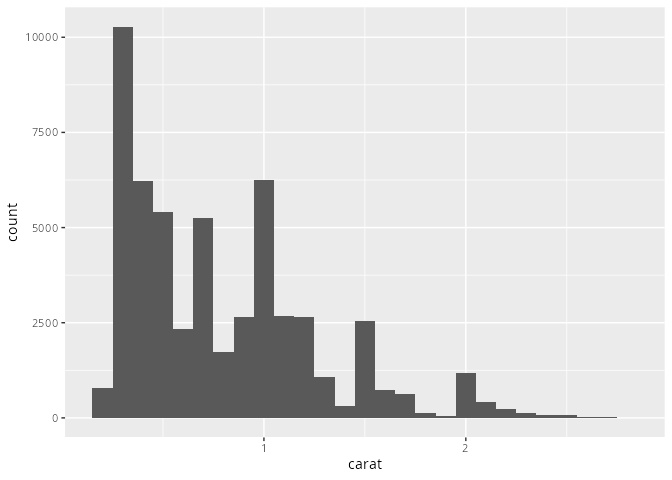

Abbildung 14.3: Kleine Balkenbreiten führen hier dazu, dass mehr Struktur, das heißt mehr Muster in den Daten zu sehen sind. Um genauer hinzusehen betrachten wir nur Diamanten, deren Gewicht kleiner als 3 Karat ist.

smaller |> ggplot(aes(x = carat)) +
           geom_histogram(binwidth = 0.01)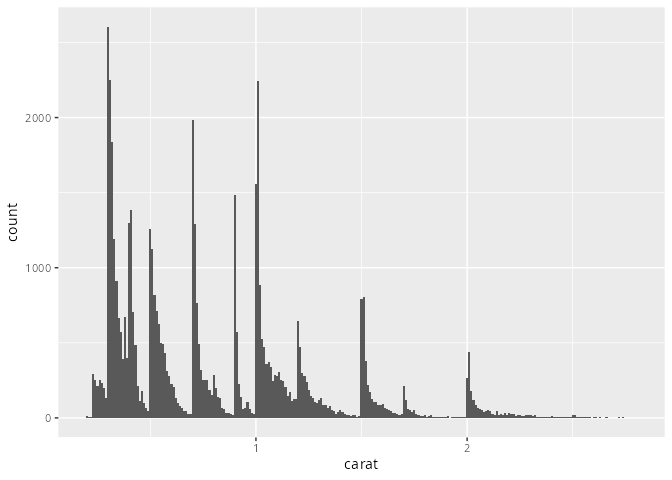

Abbildung 14.4: Histogramm mit minimal sinnvoller Breite. Die Balken haben eine Breite von 0.01, das ist die Genauigkeit mit der die Karatzahl gemessen wird. Hier sehen wir die Struktur der Karat-Verteilung sehr gut.

In Abbildung 14.3 und vor allem Abbildung 14.4 können wir erkenne, das bei kleiner Intervallbreiten die Ausprägungen in der Nähe von ganz- und halbzahligen Werten besonders häufig auftreten.

Ist man in seiner Analyse soweit vorgedrungen, so liegen nach Abbildung 14.3 einige Fragen nah, und wir können unsere Fragestellung weiter konkretisieren. Zum Beispiel

Welche sind die häufigsten vorkommenden Werte und warum sind es genau diese?
Welche Werte kommen nur selten vor und warum?
Gibt es ungewöhnliche Muster in der Verteilung?

Und in der nächsten Idteration, das heißt nach Abbildung 14.4 sind die Fragen noch konkreter, zum Beispiel

Warum gibt es mehr Diamanten mit einer ganzzahligen Karatzahl oder mit einer Karatzahl deren Bruch einfach ist (\frac{1}{4}, \frac{1}{2} oder \frac{3}{4})
Warum gibt es mehr Diamanten deren Karatzahl rechts neben den Peaks ist als links neben diesen?
Warum gibt es nur sehr wenige Diamanten, die mehr als 3 Karat wiegen?

Aufgabe: Diamanten

Stellen Sie für letzten drei der obigen Fragen Hypothesen auf und versuchen Sie die Fragen für sich zu beantworten.

Während die obigen Histogramme alle Diamanten betrachtet, könnte es auch interessant sein, das Gewicht je Schnitt darzustellen. Eine Möglichkeit dies in nur einer Grafik zu machen wäre die Funktion geom_freqpoly() mit der wir Häufigkeitspolygonzüge darstellen können. Ich persönlich würde diese Darstellung nicht überstrapazieren und nur dann verwenden, wenn es wirklich sinnvoll ist. Oft sind facettierte Histogramme die schönere Wahl.

smaller |> 
     ggplot(aes(x = carat, colour = cut)) +
     geom_freqpoly(binwidth = 0.1)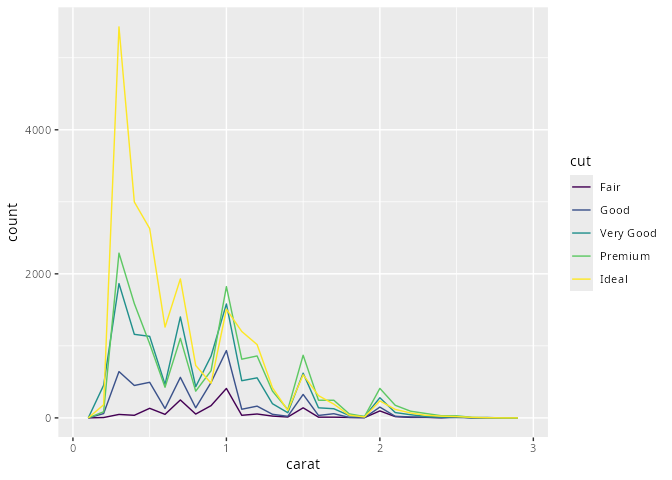

Abbildung 14.5: Häufigkeitspolygonzüge die das Gewicht (`carat`) bei verschiedenen Schliffen (`cut`) zeigen.

14.2.3 Ungewöhnliche Werte / Ausreißer

Trägt man das Merkmal y auf der x-Achse auf, so fällt die ungewöhnlich breite x-Achse auf.

diamonds |> 
    ggplot() + 
    geom_histogram(aes(x = y), 
                   binwidth = 0.5)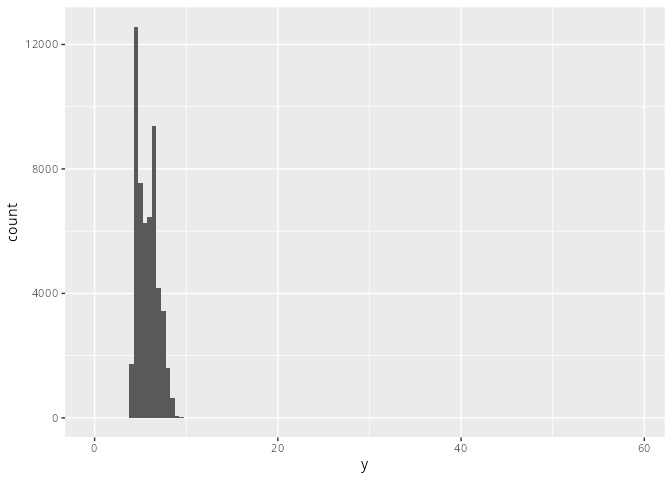

Abbildung 14.6: Histogramm des Merkmals `y`. Es fällt auf, dass die x-Achse ungewöhnlich lang ist.

Es ist nun möglich mit der Funktion coord_cartesian() in die Funktion hinein (oder hinaus) zu zoomen.

diamonds |> 
    ggplot() + 
    geom_histogram(aes(x = y), 
                   binwidth = 0.5) +
    coord_cartesian(ylim = c(0, 30)) # kleine y-Werte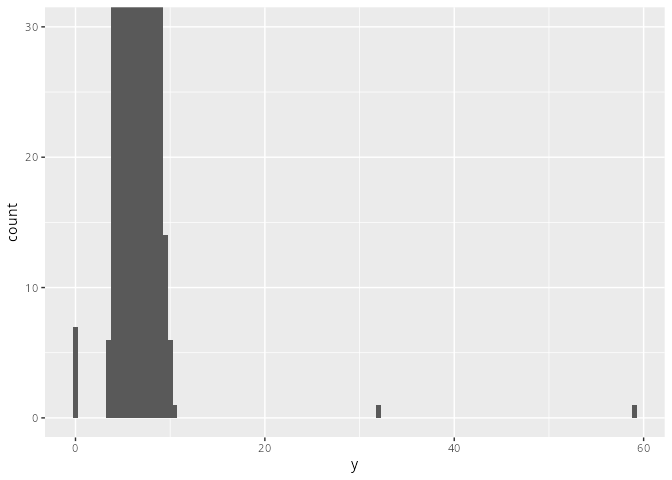

Abbildung 14.7: Mit der Funktion `coord_cartesian()` kann man in die Grafik hineinzoomen. In diesem Fall wurde y-Achse, die zuvor bis über 12000 ging auf den Bereich bis 30 gezoomt.

Nach der Vergrößerung kann man sehen, dass es für y bei 0, knapp oberhalb der 30 und knapp unterhalt der 60 noch Werte gibt.
Da x, y und z die Abmessungen der Diamanten in mm sind, ist 0 sicherlich falsch bzw. offenbar ein fehlender Eintrag.
Die beiden großen y-Werte sind offenbar auch falsche Einträge, da der Preis nicht so utopisch hoch ist, wie er für solche Diamanten sein müsste.

unusual <- diamonds |> 
              filter(y < 3 | y > 20) |> 
              select(price, cut, x, y, z) |>
              arrange(y)
unusual

# A tibble: 9 × 5
  price cut           x     y     z
  <int> <ord>     <dbl> <dbl> <dbl>
1  5139 Very Good  0      0    0   
2  6381 Fair       0      0    0   
3 12800 Ideal      0      0    0   
4 15686 Premium    0      0    0   
5 18034 Premium    0      0    0   
6  2130 Good       0      0    0   
7  2130 Good       0      0    0   
8  2075 Ideal      5.15  31.8  5.12
9 12210 Premium    8.09  58.9  8.06

Solche Ausreißer können nun mehrere Ursachen haben: oft sind es Eingabefehler, allerdings können solche Ausreißer auch neue Erkenntnis bringen. Die offensichtliche Frage, die sich nun stellt ist: “Wie geht man mit den so gewonnenen Erkenntnissen um?”

Falls in einer Datentabelle ungewöhnliche Werte auftauchen, die man als falsch identifiziert hat (oft ist das nicht einfach), so hat man im Wesentlichen zwei Möglichkeiten dies zu handhaben. In jedem Fall sollte man das Verfahren in der Auswertung dokumentieren.

Möglichkeit 1:

Man filtert die Zeilen heraus, in denen die ungewöhnlichen Werte auftauchen.

# zum Beispiel:
diamonds2 <- diamonds |> 
             filter(between(y, 3, 20))

Nach dem Filterfunktion oben bleiben nur die Diamanten übrig deren Gewicht zwischen 3 und 20 Karat liegt. Das heißt alle Ausreißer sind nicht mehr Teil des resultierenden Datensatzes.

Möglichkeit 2:

Man ersetzt die ungewöhnlichen Werte durch fehlende Werte, also NAs. Am einfachsten geht dies mit der Funktion mutate():

# zum Beispiel:
diamonds2 <- diamonds |>  
             mutate(y = ifelse(y < 3 | y > 20, NA, y))

(*) Aufgabe: NAs

Welche Vor- und Nachteile haben die beiden Möglichkeiten?

Die Auswahlfunktion ifelse()

Die Funktion ifelse(test, yes, no) hat drei notwendige Argumente:

test= ist eine Abfrage, die einen logischen Vektor liefern muss.
yes= ist das was ausgeführt wird, wenn die Abfrage in test= den Wahrheitswert TRUE hat
no= ist wird ausgeführt, falls die Abfrage in test= den Wahrheitswert FALSE hat.

Beispiel

# bei Vektoren:
x <- c(1,3,2,6,9)
y <- c(3,1,5,5,8)

x < y

[1]  TRUE FALSE  TRUE FALSE FALSE

ifelse(x < y, 
       paste(x, "ist kleiner als", y), 
       paste(x, "ist nicht kleiner als", y))

[1] "1 ist kleiner als 3"       "3 ist nicht kleiner als 1"
[3] "2 ist kleiner als 5"       "6 ist nicht kleiner als 5"
[5] "9 ist nicht kleiner als 8"

Analog funktioniert dies auch in Datentabellen. Die Funktion ifelse() wird dann benutzt, wenn man zum Beispiel einzelne Änderungen in einer Datentabelle machen möchte oder wenn man ein neues Merkmal erstellt, dessen Einträge an einem anderern Merkmal hängt.

# bei tibbles in mutate()
tib <- tibble(Name = c("Alf", "Bob", "Carl", "Doro", "Emil", "Fabi"),
              Note = c(2.0, 5.0, 4.0, 5.0, 5.0, 2.3))


tib |> mutate(Bestanden = ifelse(Note < 5, "bestanden", "nicht bestanden"))

# A tibble: 6 × 3
  Name   Note Bestanden      
  <chr> <dbl> <chr>          
1 Alf     2   bestanden      
2 Bob     5   nicht bestanden
3 Carl    4   bestanden      
4 Doro    5   nicht bestanden
5 Emil    5   nicht bestanden
6 Fabi    2.3 bestanden

# bei tibbles in mutate()
tib <- tibble(Name = c("Alf", "Bob", "Carl", "Doro", "Emil", "Fabi"),
              Anwesend = c("ja", "Ja", "nein", "Ja", "nein", "ja"))


tib |> mutate(across(Anwesend, 
                     \(XX) {ifelse(Anwesend == "Ja", "ja", XX)} ))

# A tibble: 6 × 2
  Name  Anwesend
  <chr> <chr>   
1 Alf   ja      
2 Bob   ja      
3 Carl  nein    
4 Doro  ja      
5 Emil  nein    
6 Fabi  ja

Bemerkungen

Im zweiten Beispiel ist der dritte Eintrag in der Funktion ifelse() das Argument der Funktion \(XX) (also hier XX). Dies bedeutet, dass der ursprüngliche Eintrag des Datensatzes nicht geändert wird.

Alternativ kann die Funktion case_when() aus dem Paket dplyr verwendet werden, die es erlaubt, mehr als eine Bedingung hintereinander zu prüfen und zu ersetzen. Die Syntax sieht wie folgt aus

# bei tibbles in mutate()
tib <- tibble(Name = c("Alf", "Bob", "Carl", "Doro", "Emil", "Fabi"),
              Anwesend = c("ja", "ja", "nein", "vielleicht", "nein", "ja"))

tib

# A tibble: 6 × 2
  Name  Anwesend  
  <chr> <chr>     
1 Alf   ja        
2 Bob   ja        
3 Carl  nein      
4 Doro  vielleicht
5 Emil  nein      
6 Fabi  ja

tib |> mutate(across(Anwesend, 
                     \(XX) {case_when(Anwesend == "ja" ~ 10,
                                      Anwesend == "nein" ~ 0, 
                                      Anwesend == "vielleicht" ~ 5)}))

# A tibble: 6 × 2
  Name  Anwesend
  <chr>    <dbl>
1 Alf         10
2 Bob         10
3 Carl         0
4 Doro         5
5 Emil         0
6 Fabi        10

Die verschiedenen Abfragen werden durch Kommata getrennt und was genau passieren soll steht hinter der Tilde. Im obigen Beispiel sollen bei den Einträgen Ersetzungen erfolgen.

Aufgabe: case_when()

Laden Sie das Paket DA.students und ändern Sie im Datensatz dat.studenten mit der Funktion case_when() die Einträge des Merkmals Wohnform, so dass WG zu Wohngemeinschaft wird, Appartment zu Eigene Wohnung und Eltern zu Elternhaus.

14.2.4 Umwandlung eines metrischen in eine kategoriales Merkmal

Ein metrisches Merkmal lässt sich durch Einteilung des Wertebereichs in Intervalle in ein ordinales Merkmal umwandeln. Die Ausprägungen entsprechen dann den Intervallen. Zur Einteilung in Intervalle gibt es folgende Möglichkeiten:

Gleich große Intervalle erhalten wir mit cut_width().
Ungefähr gleich viele Beobachtungen in jedem Intervall erhalten wir mit cut_number().
Beliebige Intervalle erhalten wir mit cut().
Über die Option closed bzw. right (bei cut()) können wir einstellen, ob die linke oder rechte Intervallgrenze inkludiert werden soll.

diamonds |> filter(carat<=3) |> 
            count(cut_width(carat, 1))

# A tibble: 4 × 2
  `cut_width(carat, 1)`     n
  <fct>                 <int>
1 [-0.5,0.5]            18932
2 (0.5,1.5]             29566
3 (1.5,2.5]              5316
4 (2.5,3.5]                94

diamonds |> filter(carat<=3) |> 
            count(cut_number(carat, 3))

# A tibble: 3 × 2
  `cut_number(carat, 3)`     n
  <fct>                  <int>
1 [0.2,0.5]              18932
2 (0.5,1]                17506
3 (1,3]                  17470

diamonds |> filter(carat<=3) |> 
            count(cut(carat, breaks=c(0,1,3)))

# A tibble: 2 × 2
  `cut(carat, breaks = c(0, 1, 3))`     n
  <fct>                             <int>
1 (0,1]                             36438
2 (1,3]                             17470

14.3 Kovariation

14.3.1 Ein kategoriales und ein metrisches Merkmal

Liniendiagramm

Oft möchte man die Verteilung eines metrischen Merkmals für verschiedene Kategorien vergleichen. Im Beispiel rechts die Verteilung des Preises bei verschiedenen Schnittarten.

diamonds |> ggplot(aes(x = price)) + 
            geom_freqpoly(aes(color = cut), 
                          binwidth = 500)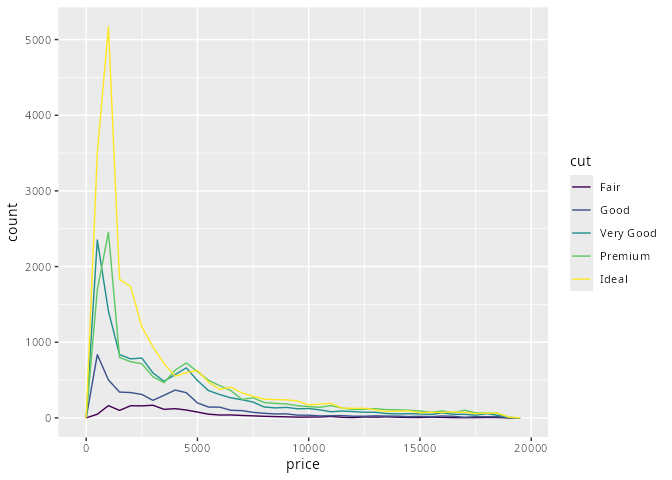

diamonds |> ggplot(aes(x = price, 
                       y = after_stat(density))) + 
            geom_freqpoly(aes(colour = cut), 
                          binwidth = 500)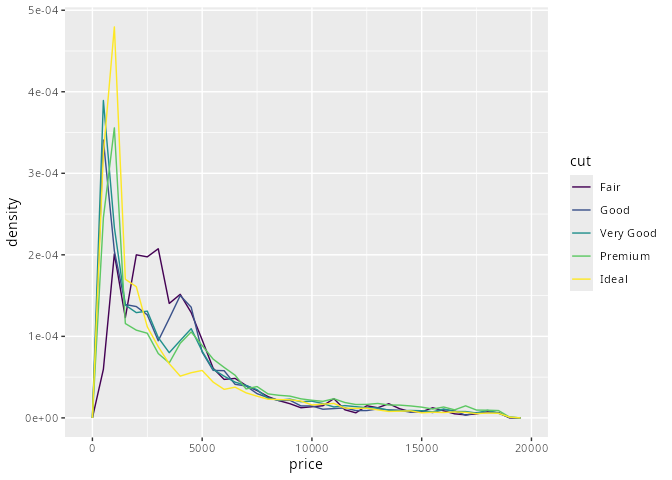

Abbildung 14.9: Häufigkeitspolygonzug, Dichte

Die Verteilungen lassen sich mit den Liniendiagrammen nur schlecht vergleichen, da die Anzahlen der Diamanten je Schnittart stark variieren (obere Grafik).
Um die Linien vergleichen zu können kann man von den Anzahlen zu Dichten übergehen (untere Grafik). Hierbei wird die Höhe der Linien so skaliert, dass die Fläche unter jedem Linienzug eins ergibt.
Wenn man die Linienzüge nun vergleicht, scheinen die die Diamanten minderer Qualität tendenziell teurer zu sein als die Diamanten guter Qualität. Ist das wirklich so oder liegt das daran, dass wir die Dichte-Liniendiagramme nicht richtig interpretieren?

Boxplot

Eine Alternative zu den Liniendiagrammen sind gruppierte Boxplots.

Die Box entspricht dem Bereich, in dem die mittleren 50% der Daten liegen. Sie wird durch das erste und dritte Quartil begrenzt. Die Länge der Box wird als Interquartilsabstand (IQA bzw. englisch IQR) bezeichnet.
Die Linie in der Box ist der Median. Der Strich teilt das Diagramm in zwei Bereiche in denen jeweils 50% der Daten liegen.
Die Schnurrbarthaare (whisker) am Ende der Box repräsentieren die Werte, die außerhalb der Box liegen und die bis zu dem 1,5-fachen des IQAs von der Box entfernt sind. Die Längen der Whisker werden also durch die Datenwerte zwischen Box und dem 1,5-fachen des IQAs bestimmt.
Die Punkte, die über bzw. unter der Whisker liegen, bezeichnet mal als Ausreißer.

diamonds |> ggplot(aes(x = cut, y = price)) +
            geom_boxplot()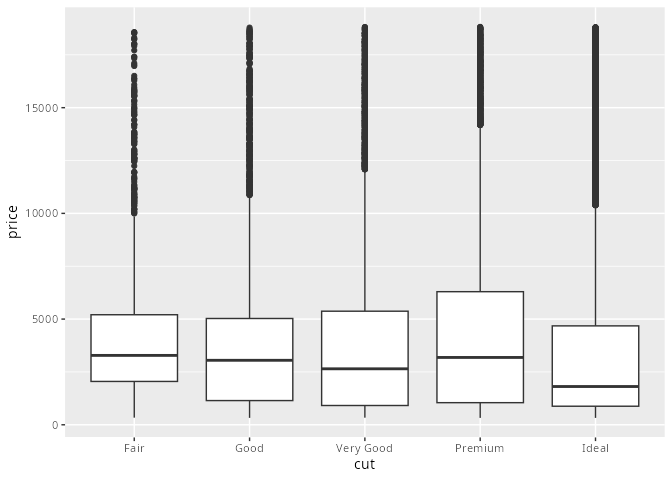

Können die Ausprägungen eines nominalen Merkmals sinnvoll geordnet werden, so spricht man von einem ordinalen Merkmal. Beispielsweise ist das Merkmal cut im letzten Plot ordinal, der Autotyp class in der Datentabelle mpg ist es nicht.
Bei ordinalen Merkmalen zeichnen wir die Boxplots in auf- oder absteigender Reihenfolge (im Beispiel von Fair nach Ideal).
Bei gewöhnlichen nominalen, nicht ordinalen Merkmalen,mkönnen wir die Reihenfolge der Ausprägungen frei wählen. Wir sollten die Reihenfolge so wählen, dass die Grafik möglichst informativ und übersichtlich ist, z.B. nach ansteigendem Median. Dies kann man mit der Funktion reorder() erreichen.
Im Beispiel werden die Boxplots zunächst unübersichtlich alphabetisch und dann übersichtlich nach dem Median sortiert dargestellt.

mpg |> ggplot(aes(x = class, y = hwy)) + 
       geom_boxplot()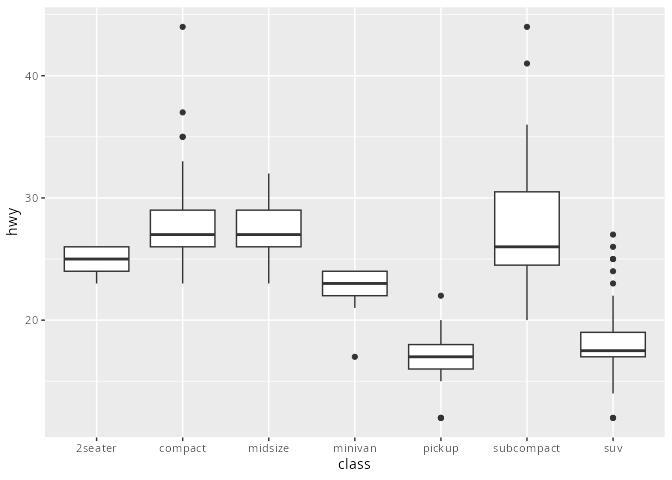

mpg |> ggplot() +
       geom_boxplot(aes(x = reorder(class, 
                                    hwy, 
                                    FUN = median), 
                        y = hwy))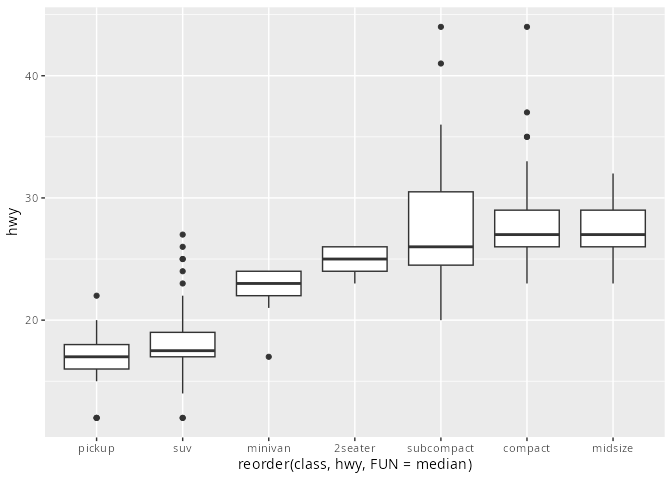

Violinplot

Eine Alternative zum Boxplot ist der Violinplot, bei dem die Verteilung der Werte durch die Breite repräsentiert wird, das heißt in einem dicken Teil befinden sich mehr Werte.
Mit der Funktion coord_flip() können die Boxplots horizontal gedreht werden, was bei langen Namen der Ausprägungen oder sehr vielen Ausprägungen zu bevorzugen ist.
Beim Umbenennen der Variablen mit der Funktion labs() spielt die Funktion coord_flip() keine Rolle. Die Einträge in den Aesthetics sind entscheidend!

mpg |> ggplot() +
       geom_boxplot(aes(x = reorder(x = class,      # kateg. zu ordnendes Merkmal  
                                    X = hwy,        # Merkmal wonach geordnet wird
                                    FUN = median),  # wie?
                        y = hwy)) + 
       labs(x = "class") +
       coord_flip()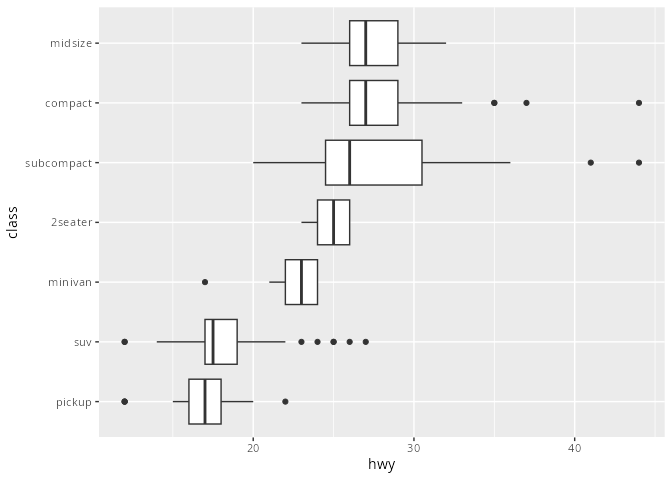

mpg |> ggplot() +
       geom_violin(aes(x = reorder(class,
                                   hwy, 
                                   FUN = median), 
                       y = hwy)) + 
       coord_flip()  +
       labs(x = "class")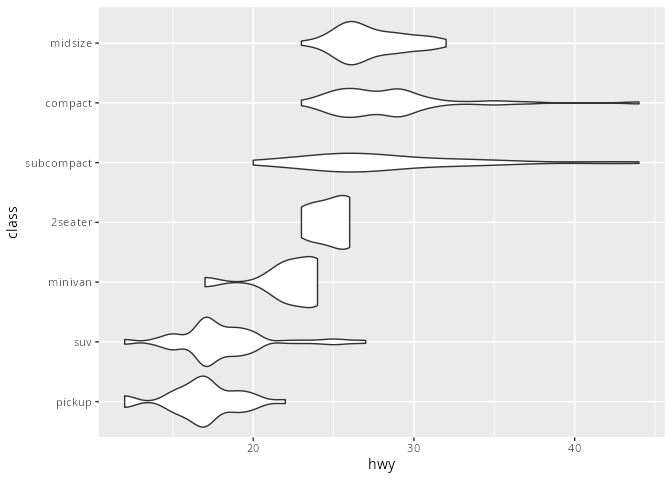

14.3.2 Zwei kategoriale Merkmale

Im Fall zweier kategorialer Merkmale muss für eine Häufigkeitsanalyse gezählt werden, wie oft jedes Beobachtungspaar vorkommt. Dies erledigt die geometrische Funktion geom_count(), bevor die Häufigkeiten durch unterschiedlich große Kreise dargestellt werden.
Mit der Funktion count() aus dem dplyr-Paket werden diese Häufigkeiten direkt bestimmt und als Datentabelle mit den Spalten color, cut und n zurückgeliefert, wobei n die zugehörige Anzahl enthält. Diese Datentabelle visualisieren wir mit der geometrischen Funktion geom_tile().

diamonds |> ggplot() +
              geom_count(aes(x = cut, y = color))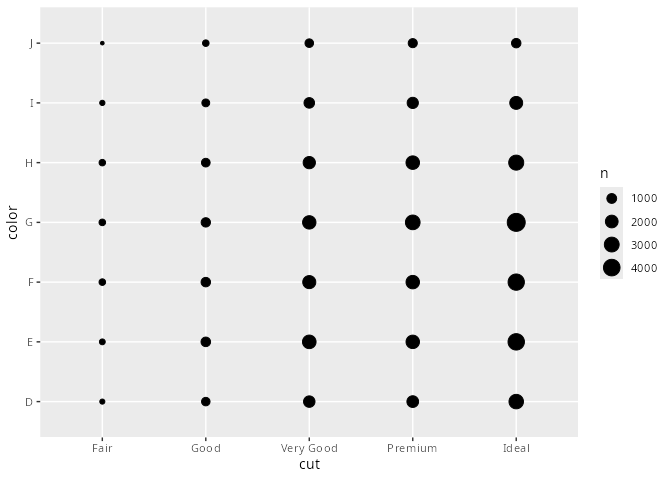

diamonds |> count(color, cut) |>  
            ggplot(aes(x = cut, y = color)) +
               geom_tile(aes(fill = n))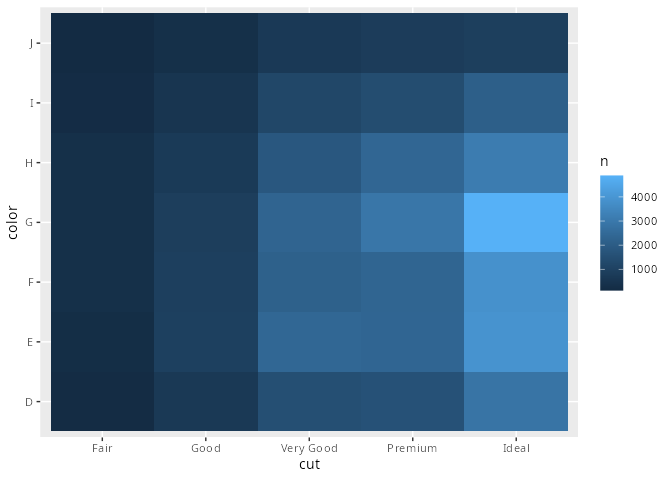

Um die Unabhängigkeit zweier Merkmale zu prüfen, ist der Mosaikplot aus dem Paket ggmosaic die richtige Wahl.
Mit dem Mosaikplot erkennt man sowohl die Verteilung der einzelnen Merkmale als auch die Verteilung des zweiten Merkmals (y-Achse) gegeben die Ausprägung des ersten Merkmals (sog. bedingten Wahrscheinlichkeiten).

library(pacman)
p_load("ggmosaic")

diamonds |> ggplot() +
    geom_mosaic(aes(x = product(cut, color), 
                    fill = cut))

mpg |> filter(manufacturer %in% 
           c("audi", "ford", "toyota", "volkswagen")) |> 
       ggplot() +                 
         geom_mosaic(aes(x = product(manufacturer, class), 
                         fill = manufacturer))

14.3.3 Zwei metrische Merkmale

Streudiagramme

Eine hervorragende Darstellung für zwei metrische Merkmale ist das Streudiagramm, das wir der geometrischen Funktion geom_point() zeichnen lassen können.
Für große Datensätze sind Streudiagramme oft wenig geeignet, da viele der Datenpunkte überlappen, und Information verloren gehen kann. Der Parameter alpha= macht Datenpunkte transparent und ist insbesondere bei mittelgroßen bis großen Datensätzen sehr nützlich.

diamonds |> ggplot() +
            geom_point(aes(x = carat, y = price))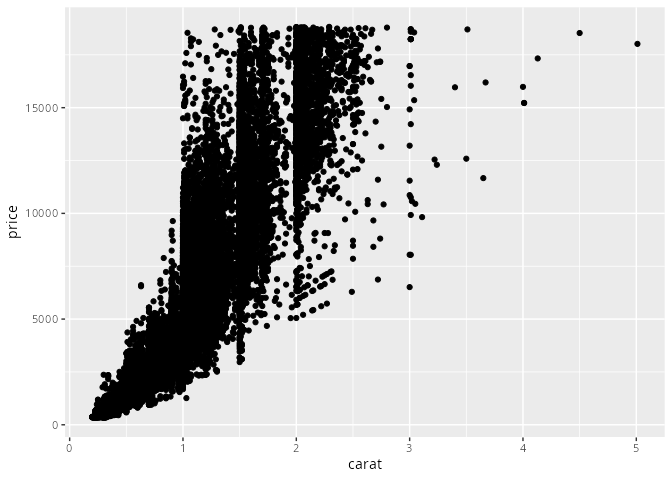

diamonds |> ggplot() +
            geom_point(aes(x = carat, y = price), 
                       alpha  = 0.01)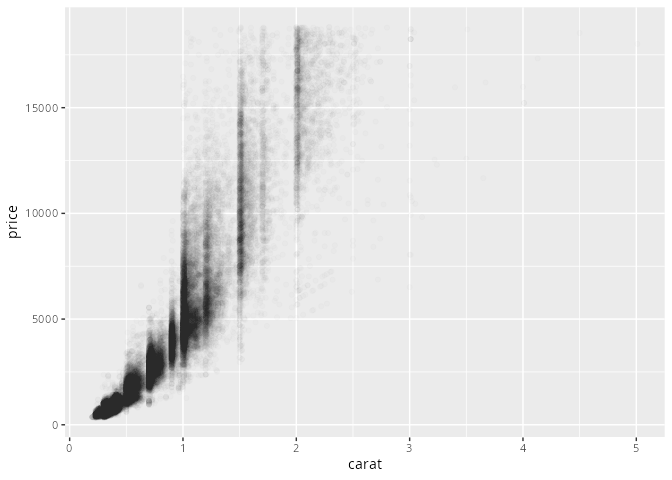

Häufigkeitsdiagramme

Die geometrischen Funktionen geom_bin2d() und geom_hex() aus dem Paket hexbin teilen die Ebene, deren Punkte die Werte der beiden metrischen Merkmale repräsentieren, in Rechtecke oder Hexagone auf. Nun wird - analog zum Histogramm - gezählt, wie viele Beobachtungen in den einzelnen Flächen liegen. Die Farbe repräsentiert diese Anzahl, die der Anzahl der Beobachtungen entspricht, die in einem Streudiagramm in der jeweiligen Fläche lägen.
Damit sind geom_bin2d() und geom_hex() die zweidimensionalen Pendants zu der eindimensionalen Funktion geom_histogram().

 smaller <- diamonds |> filter(carat < 3)

ggplot(data = smaller) +
   geom_bin2d(aes(x = carat, y = price))

library(pacman)
p_load(hexbin)

ggplot(data = smaller) +
   geom_hex(aes(x = carat, y = price))

Abbildung 14.22: Haeufigkeitsdiagramme01

Transformation in ein ordinal-skaliertes Merkmal

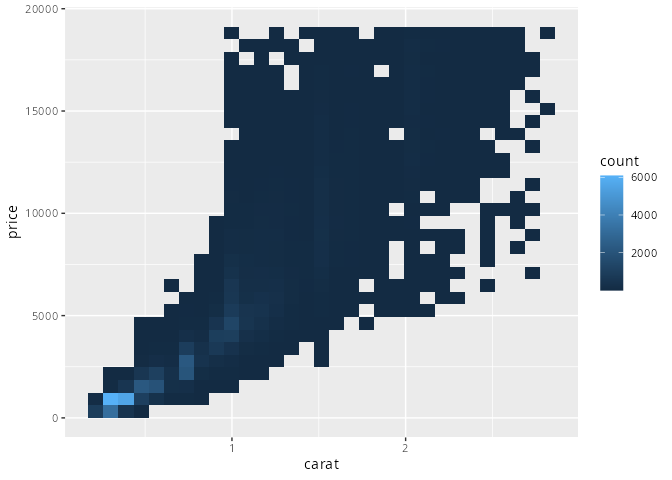
Ein metrisches Merkmal kann in ein ordinal-skaliertes Merkmal transformiert werden, in dem man die Werte in Intervalle gruppiert.
Anschließend kann der Zusammenhang zwischen dem weiterhin metrischen und dem transformierten ordinalen Merkmal durch die dafür geeigneten Grafiken dargestellt werden.
- Beispielsweise können wir gruppierte Boxplots zeichnen.
- Für die Gruppierung bieten sich folgende beiden Möglichkeiten an:
- Die Funktion cut_width() gibt eine feste Intervallbreite vor. Da die Boxen alle gleich breit sind, sieht man nicht, wie viele Datenpunkte zu einem Boxplot gehören.
- Die Funktion cut_number() gewährleistet, dass jedem Boxplot etwa gleich viele Datenpunkte zugrunde liegen.

smaller |> ggplot(aes(x = carat, y = price)) + 
           geom_boxplot(aes(group = cut_width(carat, 0.1)))

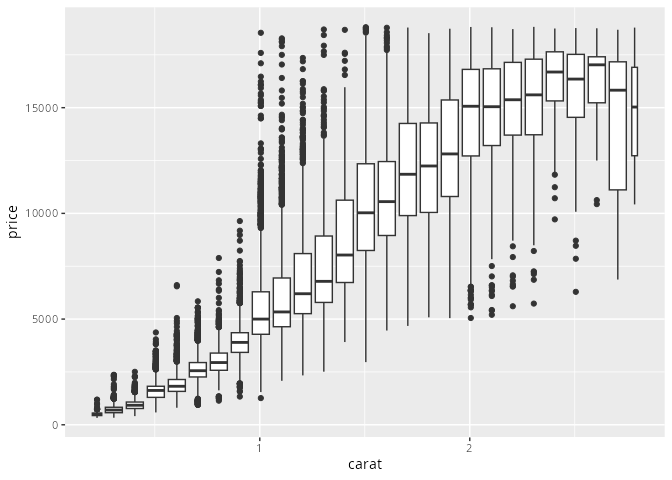
smaller |> ggplot(aes(x = carat, y = price)) + 
           geom_boxplot(aes(group = cut_number(carat, 20)))

14.4 Grafische Gesamtübersicht über eine Datentabelle

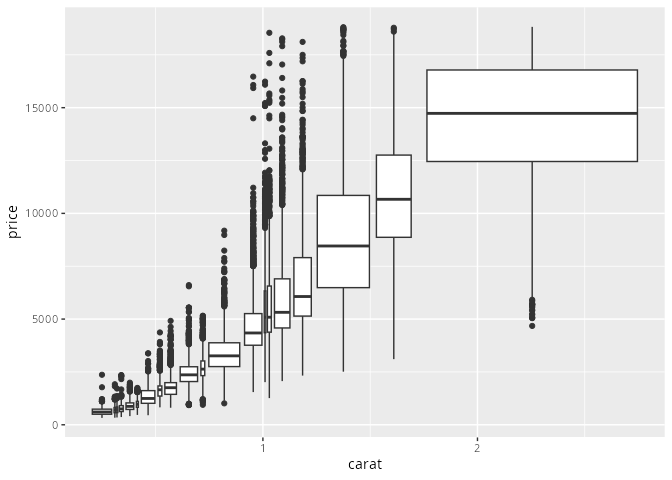
Mit Hilfe des Pakets GGally kann man eine Gesamtübersicht über eine Datentabelle erlangen. Durch die Funktion ggpairs() entsteht ein quadratisches n\times n Raster, wobei n die Anzahl der (dargestellten) Merkmale ist. Abgebildet sind

Auf der Diagonalen die Variationen, wobei bei metrischen merkmalen die Dichteverteilung angezeigt wird, bei nominalen ein Säulendiagramm.
Auf den Nicht-Diagonalen werden die Kovariationen gezeigt. Da es für jedes Paar zwei Orte gibt, wird bei metrisch/metrisch ein Streudiagramm und der Korrelationkoeffizient angezeigt, bei metrisch/kategorial die Boxplot und facettierte Histogramme und bei kategorial/kategorial facettierte Säulendiagramme und Häufigkeitsdiagramme.

library(pacman)
p_load(GGally, palmerpenguins)

penguins |>
  select(-year) |>  
  ggpairs()

14.5 Muster, Zusammenhänge und Modelle

Ein systematischer Zusammenhang zwischen zwei Merkmalen zeigt sich in einem Muster bei der Darstellung der beiden Merkmale; umgekehrt geben Muster häufig Hinweise auf einen Zusammenhang. Folgende Fragen sollten wir uns beim Auftreten solcher Muster stellen:

Kann das Auftreten des Musters Zufall sein?
Wie kann der Zusammenhang der beiden Merkmale beschrieben werden?
Wie stark ist der Zusammenhang, der durch das Muster zu erkennen ist?
Gibt es weitere Merkmale, die nicht in der Darstellung zu sehen sind, aber den Zusammenhang beeinflussen (Klassiker: Lange Studiendauer führt zu mehr Gehalt; verstecktes Merkmal: Studienfach)?
Ändert sich der Zusammenhang, wenn man nur einen Teil der Daten betrachtet?

Beispiel:

Streudiagramm zeigt auf der x-Achse die Länge der Ausbrüche und auf der y-Achse die Wartezeit bis zu dem Ausbruch des Geysirs Old Faithful im Yellowstone Nationalpark.

faithful |> ggplot(aes(x = eruptions, y = waiting)) + 
            geom_point() + 
            geom_smooth(method = "lm") + 
            labs(x = "Dauer Ausbruch [min]", y = "Wartezeit bis Ausbruch [min]")

`geom_smooth()` using formula = 'y ~ x'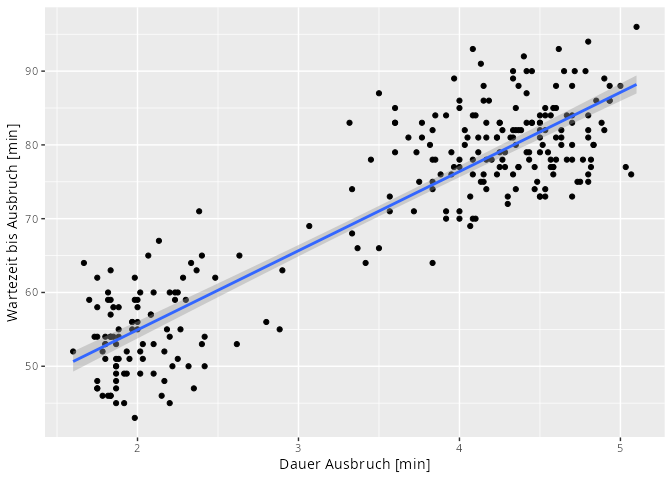

14.5.1 Scheinbare Zusammenhänge

Hohe Korrelationen heißen nicht, dass es wirklich einen Zusammenhang zwischen den beiden Merkmalen geben muss, schon gar keinen kausalen. Auf der Seite Spurious Correlations findet man stark korrelierte Merkmale, die keineswegs irgendetwas miteinander zu tun haben, wie zum Beispiel diese beiden Grafiken zeigen.

Abbildung 14.27: US spending on science, space and technology correlates with Suicides by hanging, strangulation and suffocation

Abbildung 14.28: US crude oil imports from Norway correlates with Drivers killed in collision with railway train

14.5.2 Echte Zusammenhänge

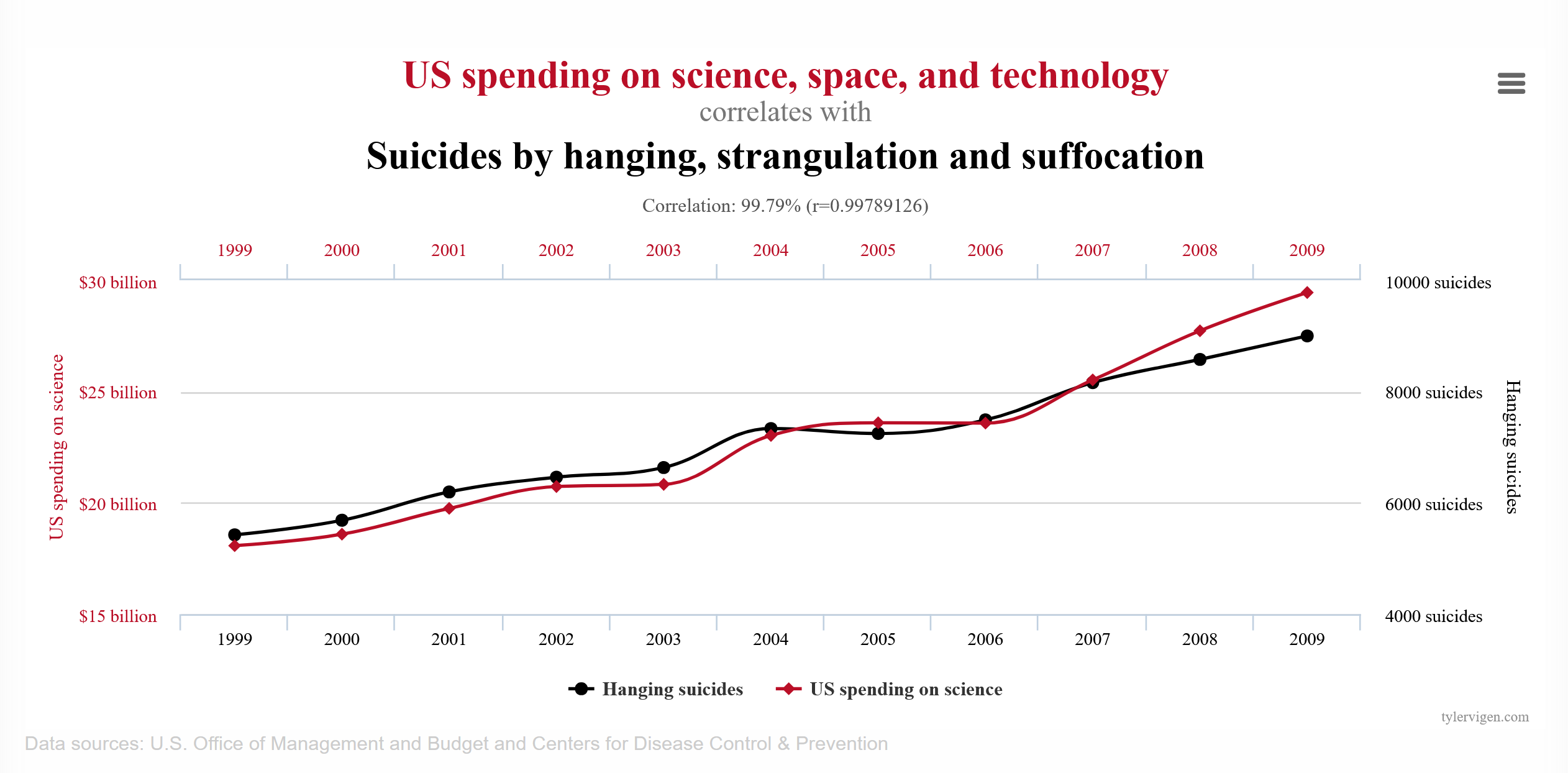
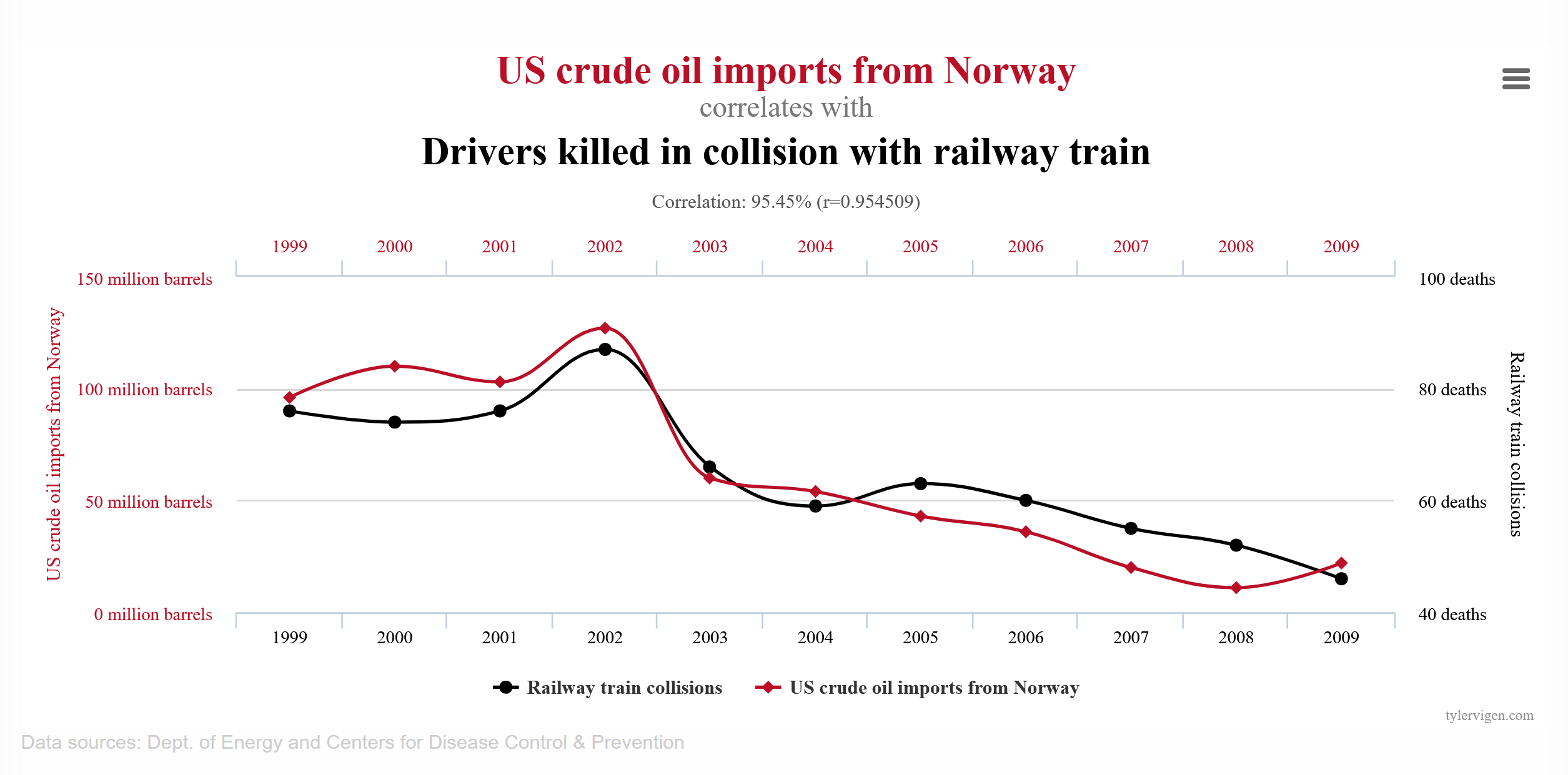
Mustererkennung hilft uns, echte Zusammenhänge, sogenannte Kovariationen, aufzudecken.
Während die Variation Unsicherheit erzeugt, verringert Kovariation die Unsicherheit.
Wenn zwei Merkmale kovariieren, können wir die Werte des einen Merkmals verwenden, um bessere Vorhersagen über die Werte des zweiten Merkmals zu treffen.
Ist die Kovariation im Spezialfall durch eine kausale Beziehung bedingt, lässt sich mit dem Wert des einen Merkmals der Wert der zweiten Merkmals steuern.

14.5.3 Modelle

Modelle sind ein Hilfsmittel, um Muster in Daten zu beschreiben.
Mit Hilfe eines solchen Modells kann ein Zusammenhang aus den Daten entfernt werden und der verbleibende Zusammenhang weiter analysiert werden.
Bei der Analyse des diamonds-Datensatz scheint der Preis mit der Güte des Schnitts zu fallen, was nicht plausibel ist (siehe obige Grafik).
Andererseits wissen wir, dass der Preis sehr stark vom Karat-Wert abhängt. Aus Gründen, die in Data Analysis 2 klar werden, analysieren wir hierbei die Abhängigkeit des logarithmierten Preises vom logarithmierten Karat-Wert (untere Grafik).
Mit einem Modell kann der Zusammenhang zwischen carat und price beschrieben werden (blaue Linie).

diamonds |> ggplot(aes(x = cut, y = price)) + 
            geom_boxplot()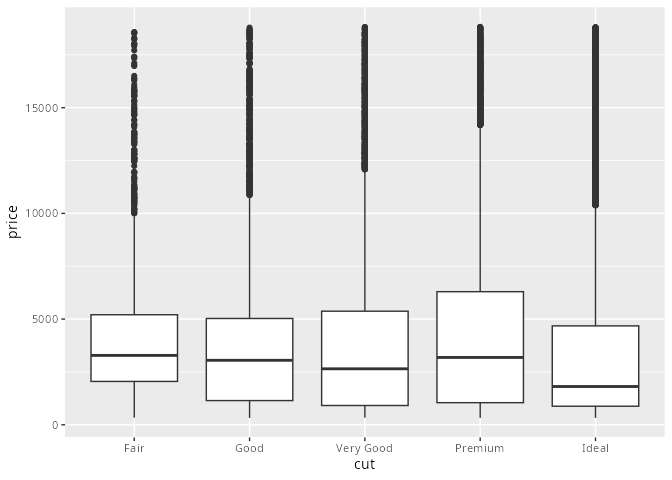

library(modelr)

mod <- lm(log(price) ~ log(carat), data = diamonds)
diamonds2 <- diamonds |> add_predictions(mod)

ggplot(data = diamonds2) +
    geom_point(aes(x = log(carat), y = log(price)), alpha = 0.2) +
    geom_line(aes(x = log(carat), y = pred), color = "blue", linewidth=0.8)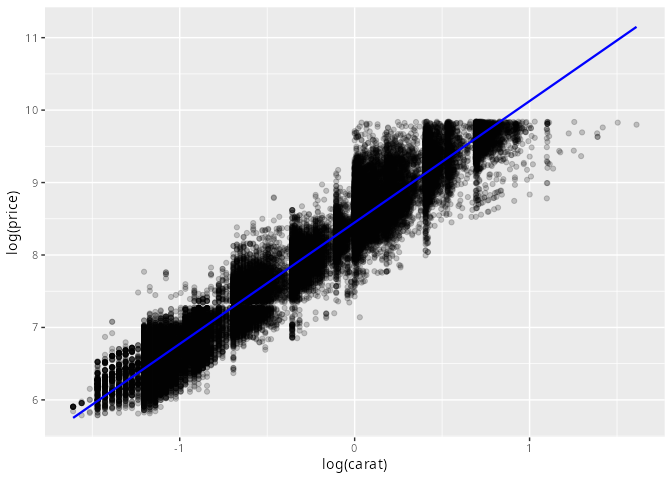

In den sog. Residuen, das ist die Differenz zwischen dem vom Modell vorhergesagten und tatsächlichen (logarithmierten) Preis, ist dieser Zusammenhang herausgerechnet (obere Grafik).
Die Residuen entsprechen den Preisschwankungen ohne den Gewichtseffekt und können weiter analysiert werden.
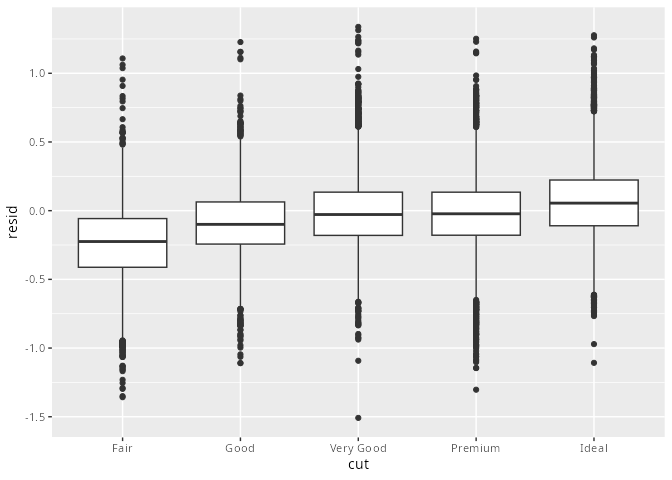
Tragen wir die Residuen über der Schnittgüte auf, erkennen wir, dass Diamanten von höherer Qualität auch teurer sind.

library(modelr)
mod <- lm(log(price) ~ log(carat), data = diamonds)
diamonds2 <- diamonds |> add_residuals(mod) # |>
                    # mutate(resid = exp(resid))

diamonds2 |> ggplot() +
             geom_point(aes(x = log(carat), y = resid),
                        alpha = 0.2)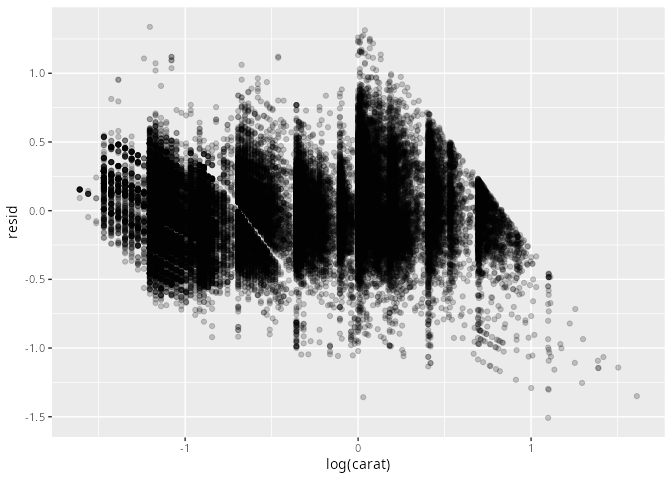

diamonds2 |> ggplot() + 
             geom_boxplot(aes(x = cut, y = resid))